2. 湖南省林业科学院,湖南 长沙 410004
2. Hunan Academy of Forestry, Changsha 410004, China
液压压榨过程中蓖麻籽可视为非线性粘弹塑性流变体[1],流变特性是蓖麻压榨理论研究的主要内容之一.目前国内外相关学者在油料力学特性方面取得了一些研究成果,张亚新等[2]建立了葵花籽压榨过程中的塑性模型,Bargale等[3]研究了大豆出油率和压榨时间的关系,但均未给出流变模型;郑晓等[4]基于蠕变试验建立了菜籽、花生和芝麻的非线性粘弹塑性模型,但并不适用于松弛试验中蓖麻籽的流变特性.本文根据蓖麻籽应力松弛试验结果,建立了蓖麻籽压榨过程中非线性粘弹塑性流变模型,并验证了模型的可靠性,从而为榨油工艺中蓖麻油流出时间的确定提供理论依据.
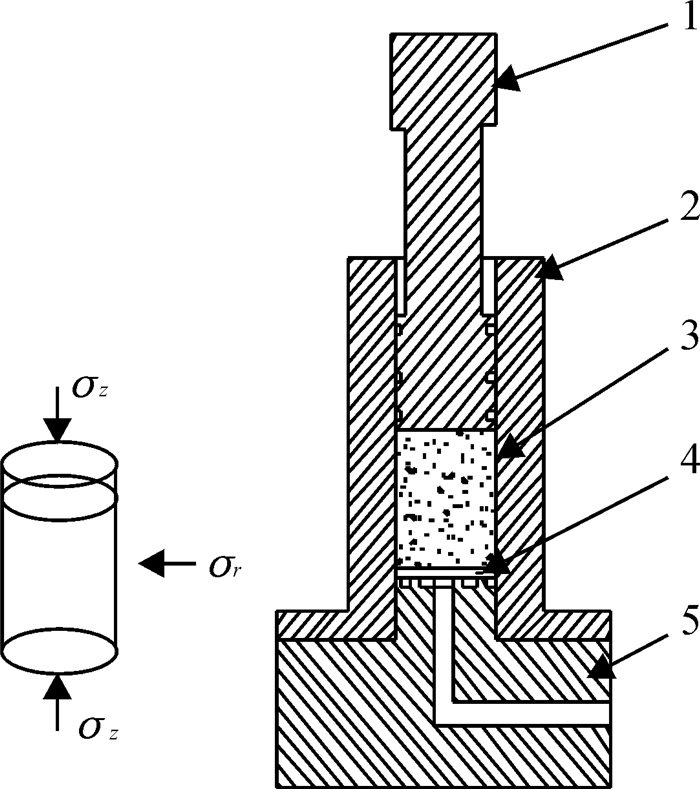
1 蓖麻籽瞬时力学特性试验 1.1 试验装置与材料该试验采用单轴压榨试验装置(图 1)、电子万能试验机和上位工控机.湖南省林业科学院培育的“湘蓖一号”蓖麻籽作为试验原料.蓖麻籽直径为6~8 mm.
|
图 1 单轴压榨试验装置 Figure 1 Uniaxial pressing apparatus 1:柱塞;2:榨筒;3:蓖麻籽;4:透水石;5:底座. |
将蓖麻籽装入单轴压榨试验装置,每组试验装入蓖麻籽高度为75 mm,共3组.利用电子万能试验机加载单轴压榨试验装置,加载速度为55 mm·min-1, 并用上位机读取万能试验机的压力值及试验装置柱塞的位移.
1.3 试验结果与分析由轴向应力σ与轴向应变ε定义有:
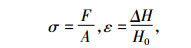
|
式中F为电子万能试验机加载压力(N),A为柱塞面积(1 194.6 mm2),H0为压榨前蓖麻籽原始高度(mm),ΔH单轴压榨试验装置柱塞位移(mm),代入试验数据得瞬时轴向应力与应变关系曲线, 见图 2.
|
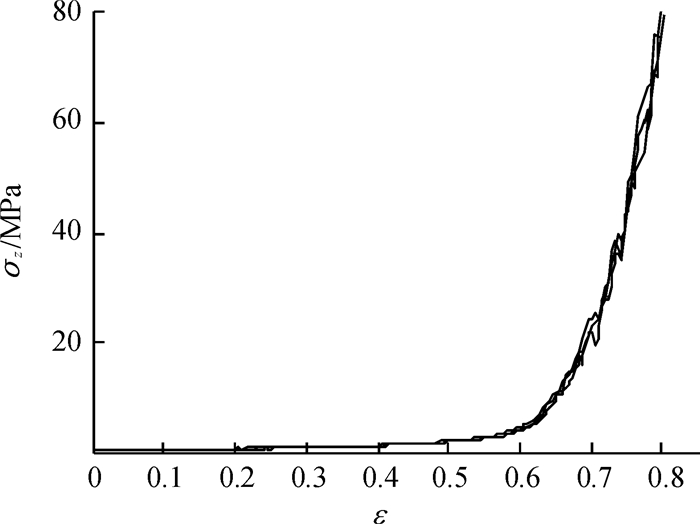
图 2 瞬时应力-应变(σ-ε)曲线 Figure 2 The instantaneous curve of stress-strain(σ-ε) |
从图 2可知,该3组试验重复性较好;压榨过程中,蓖麻籽在应变小于0.55时,应力与应变基本呈线性关系;应变大于0.55时,蓖麻籽发生塑性变形且伴随着油脂的渗出,加载过程中由于油脂不能及时流出而加快了应力增加速度,因此轴向应力与应变呈现幂次增长关系;在此定义屈服应变为系统达到屈服状态时的应变[5].蓖麻籽屈服应变(εs)为0.55,对应的屈服应力约为3.5 MPa;为更好地获取应力松弛等时曲线,由图 2可确定应力松弛试验加载应变水平分别为0.20、0.30、0.40、0.50、0.55、0.60、0.65、0.70和0.75.
2 蓖麻籽流变试验在流变试验中,应力松弛试验和蠕变试验是等价的,松弛和蠕变是同一物理性质的不同表现形式[6],蠕变试验条件是应力恒定,而松弛试验则是应变恒定,对于油料压榨过程,恒定应变能更容易实现,为提高数据的可靠性, 本研究采用应力松弛试验.
2.1 试验方法试验装置及试验材料与瞬时力学特性试验相同.应用分别加载试验方法[7-8],利用电子万能试验机对每组装有蓖麻籽的单轴压榨试验装置分别进行加载(加载速度与上述力学特性试验相同),使每组试验应变分别达到0.20、0.30、0.40、0.50、0.55、0.60、0.65、0.70、0.75,各应变水平保持30 min不变,每间隔3 min读取电子万能试验机的压力值.
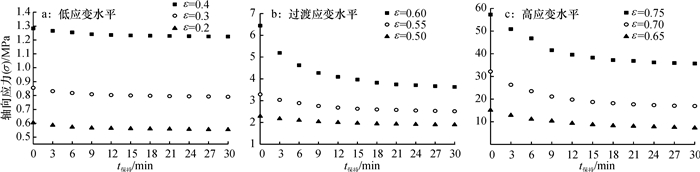
2.2 试验结果与分析将上位机采集试验数据代入轴向应力定义式,得到蓖麻籽应力松弛试验结果,各个应变水平轴向应力与时间关系如图 3所示.
|
图 3 不同应变水平松弛曲线 Figure 3 The curve of stress-relaxation under different strain levels |
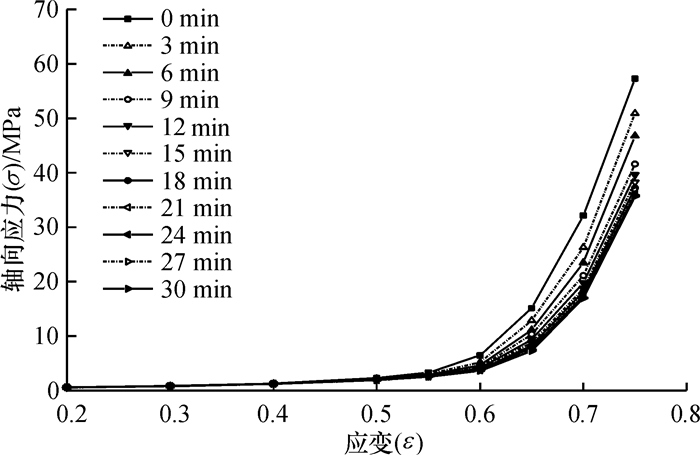
通过对图 3分析可知,蓖麻籽应力松弛过程大致由快速松弛、缓慢平稳松弛2个阶段构成,快速松弛阶段蓖麻籽承受较大的外力,蓖麻籽在榨筒中滑动,且伴随着油脂流出榨筒,随着滑动和油脂的流出,应力逐渐减小,从而导致滑动和油脂流动减缓,因此应力在该阶段松弛较快,后阶段松弛比较平稳缓慢,且随时间推移呈现基本水平趋势;同时可知,在应变小于屈服应变时,等时长内应力松弛量(即轴向应力变化量)较小,反之较大,这是由于在应变大于屈服应变后,蓖麻籽开始破裂渗出油脂,油脂随油道流出单轴压榨试验装置导致应力松弛量较大,且应变越大,应力松弛量越大.通过对图 4应力应变等时曲线分析可知,在应变小于屈服应变时,应力应变基本呈现出线性关系,应变大于屈服应变时,应力应变呈现出非线性特征,这与瞬时力学特性试验结果基本吻合.
|
图 4 应力应变等时曲线 Figure 4 The isochronous curve of stress-strain |
为使模型既能描述非线性问题又具有一定物理意义,本研究采用半理论半经验法建立非线性流变模型.对于线性段,利用模型理论建立线性粘弹性模型;对于非线性段,利用经验模型建立非线性粘塑性模型;根据流变模型并联应力叠加原理[9]可得非线性流变模型.
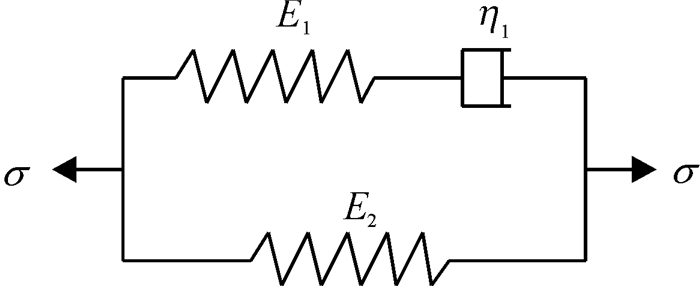
3.1 非线性粘弹塑性模型的建立根据上述瞬时力学特性试验结果和流变试验应力应变等时曲线分析结果,可知在应变小于屈服应变0.55时,应力与应变基本是线性关系,该阶段可利用线性粘弹性模型描述.因松弛试验是恒应变,采用并联式模型将有利于分析研究,在并联式模型中广义Maxwell模型被广泛用于固体材料应力松弛表述,且能较为真实反映其应力松弛特性[10].同时由松弛试验结果可知该阶段应力松弛量较小,残余应力小且不为0,可采用三元件广义Maxwell模型模拟该线性段,如图 5所示.
|
图 5 三元件广义Maxwell模型 Figure 5 Generalized Maxwell model of three elements Ei:弹性模量;η1:粘性系数. |
根据试验结果,在应变大于屈服应变0.55时,应力与应变呈现出明显非线性关系.但广义Maxwell模型只能描述线性阶段流变特性,并未含有塑性元件,不能描述压榨过程中塑性阶段的应力应变关系,同时也不能描述屈服后的应力应变的非线性关系,因此需要对模型进行改进,需加入塑性元件使其能表述材料塑性特性,加入经验模型使其能描述非线性应力应变关系.
根据应力松弛试验方法,可见试验过程中控制的变量是应变,因此加入的塑性元件也需要与应变为变量.根据屈服应变的定义,以及类似应力型塑性元件的定义[9],在此定义应变型塑性元件为系统应变达到屈服应变时便开始产生塑性应力的模型,其本构方程如下:
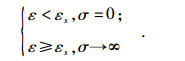
|
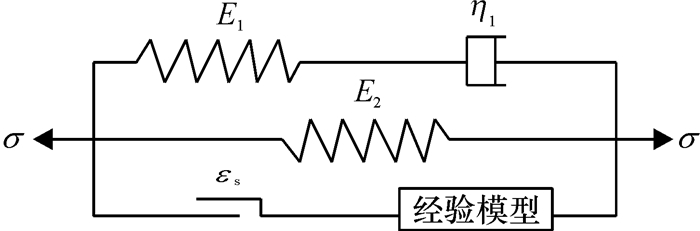
当达到屈服时,应力型塑性元件的应变等于其并联支路的应变[9],应变型塑性元件的应力等于与该元件串联支路的应力.根据模型元件串并联原理[9],加入塑性元件及经验模型得改进后的广义Maxwell模型(图 6).根据应变型塑性元件的性质可知,当应变小于屈服应变时,该模型塑性元件应力为0,经验模型未受力,图 6所示模型可视为图 5的广义Maxwell模型;当应变大于屈服应变时,该模型塑性元件应力不再为0,模型加入了经验模型,此时图 6所示模型能描述应力应变非线性关系.
|
图 6 非线性粘弹塑性模型 Figure 6 The nonlinear visco-elasticity plasticity model εs:屈服应变. |
根据上述模型的建立过程可知,除经验模型环节以外,图 6非线性粘弹塑性模型中的参数可由图 5线性阶段粘弹性模型求解出;对于经验模型环节,根据试验结果回归得到经验公式参数.在应变小于屈服应变的线性粘弹性阶段,图 6非线性模型等效于图 5所示广义Maxwell模型,设其E1、E2对应支路应力分别为σ1、σ2,由并联叠加原理可得图 5所示系统总应力:
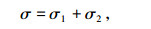
|
同理,对于应变大于屈服应变的非线性粘弹塑性阶段,图 5所示系统的总应力为:
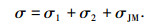
|
式中σJM为经验模型应力值.
3.2.1 线性阶段本构方程的求解根据上述分析可知,当应变小于屈服应变时,线性阶段模型可用如图 5所示的三元件广义Maxwell模型表示,该模型由1个Maxwell模型和1个弹性元件并联组成,其中Maxwell模型的本构方程为:
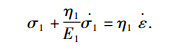
|
松弛试验中应变恒定不变,解得Maxwell模型应力松弛方程为:
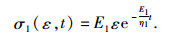
|
弹性元件E2支路方程为:σ2(ε)=E2ε.
线性阶段应力松弛本构方程为:
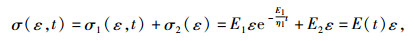
|
式中,t为松弛试验恒定应变保持时间,E(t)为松弛模量,由上式得:
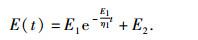
|
根据线性阶段本构方程式可知,E(t)等于图 4中相应时间t对应的应力应变等时曲线中直线段的斜率(即应变小于屈服应变0.55的直线段),根据应力松弛试验直线段数据拟合得到如表 1所示的各等时曲线直线段斜率,表中拟合相关系数都在0.88以上,可知线性段应力应变高度线性相关.
|
|
表 1 各等时曲线中直线段拟合斜率 Table 1 The fitted slope of linear segment of each isochronous curve |
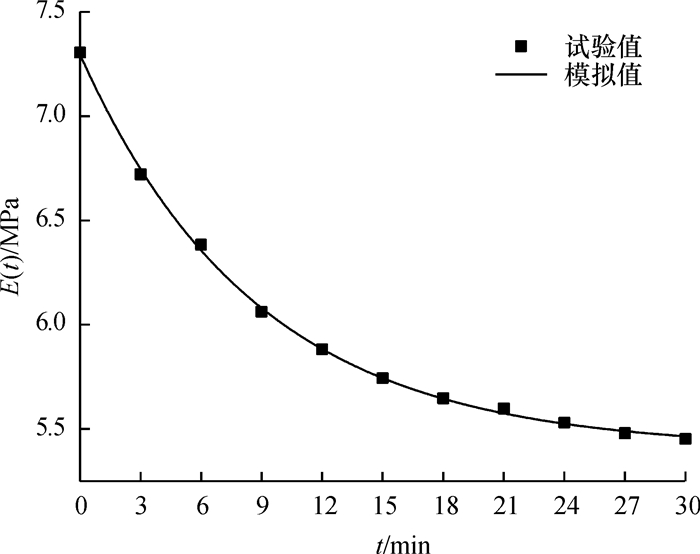
根据松弛模量表达式,代入松弛模量试验值(即表 1中斜率)和对应时间,按最小二乘法构建目标函数,并利用Levenberg-Marquardt算法[11-12]求解目标函数从而得到弹性模量E1和E2分别为1.893 0和5.403 5MPa,粘性系数η1为16.553 4MPa·min;同时可得松弛模量试验值与松弛模式表达式模拟值的对比关系如图 7所示,由图可知该回归算法精度较高,同时也验证了松弛模量表达式能较好模拟线性段的松弛模量.
|
图 7 线性段松弛模量 Figure 7 The relaxation modulus of linear segment |
为求解经验模型,将非线性模型中经验模型支路从非线性粘弹塑性模型中分离出来,如图 8所示.
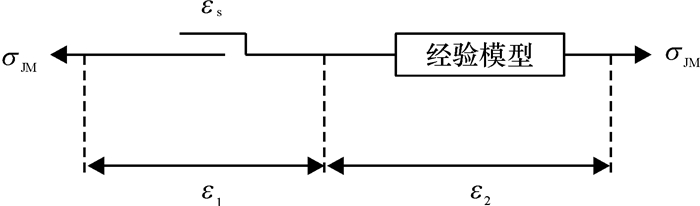
|
图 8 经验模型支路 Figure 8 The branch of empirical model |
由图 8和应变型塑性元件性质可知,当达到屈服后有:
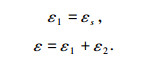
|
由流变试验等时曲线,可知应力为瞬时应力值与应力松弛量之差,即可设:
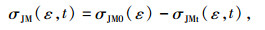
|
式中,σJM0为t=0时瞬时应力值,σJMt为非零时刻t对应应力松弛量.
根据瞬时力学特性试验结果及流变试验等时曲线,应力应变非线性发生在应变大于屈服应变段,且在此段轴向应力较大,蓖麻籽之间间隙基本被变形的蓖麻籽填充,因此这段与粉体压制成型相似,可利用粉体压制成型过程中应力应变经验模型来建立蓖麻散体在高压段非线性模型.其中川北压制模型在模拟粉体压制过程应力和应变关系时有着较高的精度[13-14],故利用川北压制方程并根据塑性元件性质得瞬时应力为:
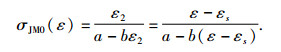
|
由流变试验结果可知,应力松弛量是应变ε和时间t的函数,故可设非零时刻t应力松弛量为:
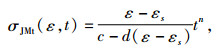
|
式中a、b、c、d、n为经验模型参数.
联立总应力公式,Maxwell模型应力松弛方程和弹性元件E2支路方程并代入流变试验数据可得经验模型应力σJM(ε, t)值.根据以上公式并利用线性段参数求解算法和基于最小二乘法的多元非线性回归[12]可解得经验模型参数a、b、c、d、n的值分别为0.012 6、0.044 0、0.066 6、0.158 2和0.398 1.同时也可得到非零时刻t应力松弛的σJMt值(图 9).
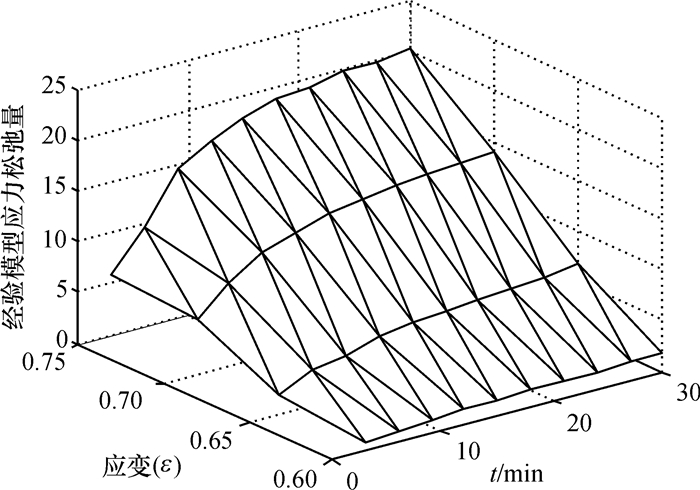
|
图 9 经验模型应力松弛量 Figure 9 The stress relaxation value of empirical model |
综上,得蓖麻籽压榨过程中非线性流变本构模型:
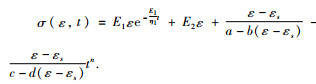
|
根据模型推导过程中运用到川北压制方程可知,该模型适用于描述蓖麻籽压榨应变达到相对较大时的流变过程.
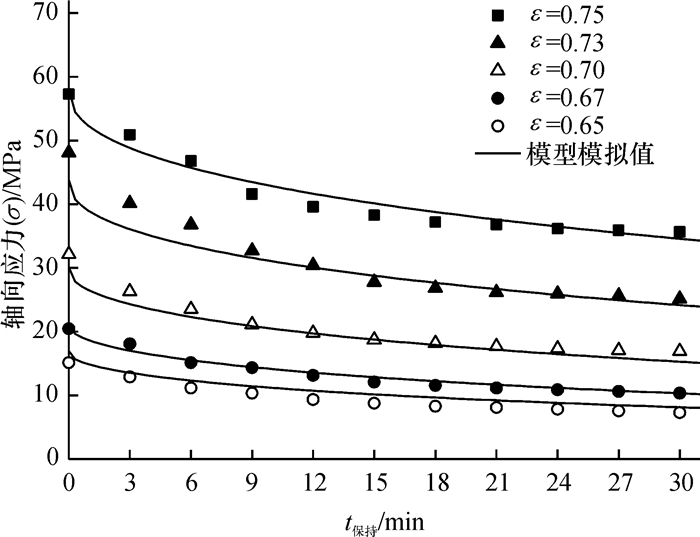
3.3 非线性流变模型的验证利用非线性流变模型分别模拟蓖麻籽压榨应变水平为0.65、0.67、0.70、0.73、0.75的应力松弛规律,模拟结果如图 10所示.为提高验证的合理性,做2组应变水平分别为0.67和0.73的流变试验结合前面所做试验数据与模拟结果对比,如图 10所示.
|
图 10 松弛试验与非线性理论模型对比 Figure 10 The comparison of stress-relaxation value and nonlinear model |
应变水平0.65、0.67、0.70、0.73、0.75对应的平均相对误差分别为12.27%、3.37%、4.30%、4.44%和3.06%.应变大于0.65后的平均相对误差均小于4.50%,相对都较小,这是由于非线性流变本构模型给出的蓖麻籽压榨非线性流变模型引入了粉体压制方程,在应变大于0.65时应力已大于10 MPa,远大于屈服应力,榨筒中的蓖麻籽之间的间隙已被变形的蓖麻籽填充,此时能更好地近似于粉体压制过程,该非线性流变模型能更好地模拟蓖麻籽该段压榨过程,故该模型适用于描述压榨应变大于0.65时蓖麻籽的流变特性.
4 结论综合应力松弛试验结果可知蓖麻籽在压榨过程呈现出非线性流变的性质, 同时在快速松弛阶段,松弛速度较快且其呈现递减趋势,最终松弛速度趋近于0达到平稳松弛阶段,由试验结果可知各应变水平的快速松弛阶段历时约12 min;结合模型验证结果可知,基于改进后的广义Maxwell模型和川北压制方程建立的非线性流变模型,能较好地模拟蓖麻籽散体在压榨应变大于0.65段的应力松弛特性,为后续蓖麻压榨保压问题的研究以及部分榨油机构设计奠定了理论依据.
| [1] |
郑晓. 油料压榨理论与试验研究[D]. 武汉: 武汉理工大学, 2005.
(  0) 0) |
| [2] |
张亚新. 植物油料压榨的塑性本构模型及有限元模拟分析[D]. 武汉: 武汉工业学院, 2009.
(  0) 0) |
| [3] |
BARGALE P C. Mechanical oil expression from selected oilseeds under uniaxial compression[D]. Saskatchewan: University of Saskatchewan, 1997.
(  0) 0) |
| [4] |
郑晓, 林国祥, 李智, 等. 菜籽与菜籽仁的非线性粘弹塑性本构模型[J]. 农业机械学报, 2005, 36(11): 87-91. DOI:10.3969/j.issn.1000-1298.2005.11.022 (  0) 0) |
| [5] |
汪训流, 陆新征, 叶列平. 往复荷载下钢筋混凝土柱受力性能的数值模拟[J]. 工程力学, 2007, 24(12): 76-81. DOI:10.3969/j.issn.1000-4750.2007.12.014 (  0) 0) |
| [6] |
罗迎社. 金属流变成形的理论, 实验与应用研究[D]. 长沙: 国防科学技术大学, 2000.
(  0) 0) |
| [7] |
于怀昌, 周敏, 刘汉东, 等. 粉砂质泥岩三轴压缩应力松弛特性试验研究[J]. 岩石力学与工程学报, 2011, 30(4): 803-811. (  0) 0) |
| [8] |
高洪梅, 刘汉龙, 刘金元. EPS颗粒轻质混合土蠕变特性试验研究[J]. 河海大学学报:自然科学版, 2010, 38(4): 402-406. (  0) 0) |
| [9] |
蔡美峰. 岩石力学与工程[M]. 北京: 科学出版社, 2002: 200-203.
(  0) 0) |
| [10] |
冯上环, 赵有科. 木材应力松弛特性及其影响因素概述[J]. 木材加工机械, 2010(3): 37-40. DOI:10.3969/j.issn.1001-036X.2010.03.009 (  0) 0) |
| [11] |
刘志平, 石林英. 最小二乘法原理及其MATLAB实现[J]. 中国西部科技, 2008, 7(17): 33-34. DOI:10.3969/j.issn.1671-6396.2008.17.015 (  0) 0) |
| [12] |
陈淑铭, 乔田田. 一个求解非线性最小二乘问题的新方法[J]. 烟台大学学报:自然科学与工程版, 2004, 17(1): 14-22. (  0) 0) |
| [13] |
郑晓, 李智, 林国祥, 等. 菜籽与脱皮菜籽冷榨的应力应变关系研究[J]. 农机化研究, 2004(6): 187-189. DOI:10.3969/j.issn.1003-188X.2004.06.070 (  0) 0) |
| [14] |
葛荣德. 川北公夫粉末压制方程应用中的几个问题及方程的修正[J]. 粉末冶金技术, 1993, 11(2): 90-94. (  0) 0) |
 2015, Vol. 36
2015, Vol. 36



