2. 广西壮族自治区植保总站,广西 南宁 530022;
3. 广西壮族自治区全州县农业局,广西 全州 541500
2. Plant Protection Station of Guangxi Zhuang Autonomous Region, Nanning 530022, China;
3. Agriculture Bureau of Quanzhou County in Guangxi Zhuang Autonomous Region, Quanzhou 541500, China
稻水象甲Lissorhoptrus oryzophilus Kuschel是全球百种最具威胁性的有害入侵生物之一[1]。截止到2011年,该虫在我国已蔓延至21个省、自治区、直辖市[2],严重影响了我国的水稻生产安全。广西于2013年在全州县发现稻水象甲的严重危害,对全区的水稻生产造成极大的威胁。
空间分布是昆虫种群的重要生态学特性之一[3]。目前已有一些稻水象甲空分布型及抽样技术研究的报道,涉及我国河北、辽宁、浙江、福建、江西、贵州等地,包括成虫、蛹、幼虫、卵等的分布情况[3-8]。鲜见不同移栽方式下的稻水象甲幼虫田间分布规律的研究。水稻移栽方式主要有抛秧和人工插秧2种。与人工插秧相比,抛秧秧苗活蔸快,没有明显的返青期;分蘖发生早、节位低、数量多;根系发达入土浅[9],秧田操作简单方便、省时、省工、省力、高产、高效等。本试验于2014年通过取样调查研究具有明显种植优势的抛秧与传统的人工插秧对稻水象甲幼虫田间空间分布的影响及其抽样技术,以期为稻水象甲的虫情调查、预测预报和综合防治提供科学依据。
1 材料与方法 1.1 试验区概况试验区设在广西桂林市全州县稻水象甲严重发生的全州镇。全州县位于广西自治区东北部,东经111°45′、北纬25°56′,属于亚热带季风湿润性气候,全年无霜期298 d,平均气温17.7 ℃,平均降雨量1 492.2 mm,雨季集中在4—8月,年平均相对湿度78%,年平均日照1 488.7 h。
1.2 方法抛秧是先把露白的种子播于塑料秧盘中进行育秧,秧龄达15~20 d后,将其抛向大田;插秧为农民广泛采用的传统插秧方法,秧龄30~40 d。抛秧一般在4月下旬,插秧在5月上中旬。
1.2.1 取样方法于2014年5月中下旬,早稻田幼虫量达高峰期时进行取样调查。在抛秧田与插秧田各选取长势一致的5块未防治的田块,平均面积约为3 000 m2。采用平行线取样法,每块田均分为11等分,即11行11列,行列交汇处取1丛水稻,共121丛,按取样位置编号并绘制田间实际分布坐标图[10]。调查时将每丛水稻连根带泥挖起,并装入样品袋内,用40~60目纱网对所取样品反复冲洗,水中放少量盐,幼虫漂浮于水面上,统计幼虫数量,并按编号记录。
1.2.2 空间分布型测定统计调查数据,计算稻水象甲幼虫平均密度值(m)、方差(S2)、平均拥挤度(m*)。采用聚集度指标法计算扩散系数(C)、聚集度指数(m/m*)、负二项分布k值,并分析稻水象甲幼虫的空间分布型;以Iwao线性回归模型m*=α+βm和Taylor幂指数法则lgS2=lga+blgm分析稻水象甲幼虫的分布格局及内部结构;用种群聚集均数(λ)分析聚集原因[11-13]。
1.3 抽样技术将调查结果绘制成坐标图,分别采用棋盘式、平行线式、双对角线式、五点取样式和Z字形取样式抽取同样的样本数进行调查。采用平均数标准误与变异系数比较抽样方法的准确度[14]:标准误越小,说明该抽样方法与田间实际情况越接近;变异系数越小,说明该抽样方法的结果变异程度越小,有代表性。
理论抽样模型[15]:在抛秧与插秧两者的m*-m回归方程前提下,根据Iwao提出的理论抽样原理确定最适理论抽样数:
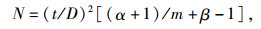
|
式中,t为95%置信度下的正态离差值,D为允许误差值,m为稻水象甲幼虫的平均密度,α、β为m*-m回归模型中的常数值。
1.4 统计分析所获数据采用Excel 2007和SPSS 20.0进行处理,用邓肯氏多重比较法(DMRT)进行差异显著性分析。
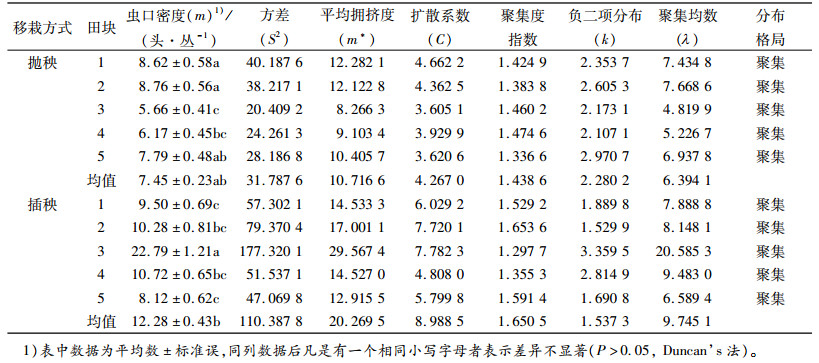
2 结果与分析 2.1 抛秧和插秧移栽方式下稻水象甲幼虫的空间分布型 2.1.1 聚集度指标测定法通过调查数据的聚集强度分析,将稻水象甲幼虫的分布聚集度指标列于表 1。各调查田块的聚集指标:扩散系数(C)与聚集度指数(m/m*)均大于1,负二项分布k值均大于0,说明所调查的抛秧田和插秧田中稻水象甲幼虫均呈聚集分布格局,且聚集强度随虫口密度上升而增加。
|
|
表 1 稻水象甲幼虫空间分布型的聚集度指标 Table 1 Aggregation indices of spatial distribution of Lissorhoptnes oryzophilus larvae |
Waters(1959)认为k值与虫口密度无关,k值越小,种群的聚集度越大,k值趋于+∞时(>8),则接近Poisson分布。表 1中,抛秧与插秧2种移栽方式下的k值为1.393 6~3.359 5,因此,抛秧与插秧田稻水象甲幼虫的分布型均不符合Poisson分布,且前者的聚集强度比后者小。
2.1.2 Iwao回归模型法根据Iwao m*-m线性回归关系m*=α+βm,得抛秧田的回归方程m*=1.256+1.240m(R=0.983 9**), 插秧田的回归方程m*=3.878+1.126m(R=0.987 9**)。截距α分别为1.256与3.878,均大于0,可认为2种移栽方式下稻水象甲幼虫在田间的分布为个体群;斜率值β分别为1.240与1.126,均大于1,表明其均呈聚集分布。
2.1.3 Taylor幂法则根据Taylor幂指数法则,以lgS2和lgm进行线性回归lgS2=lga+blgm,得抛秧田幼虫的回归方程lgS2=0.252+1.407 lgm(R=0.960 7**),插秧田的回归方程lgS2=0.507+1.277 lgm(R=0.947 7**)。两者的a分别为0.252与0.507,均大于0;b分别为1.407与1.277,均大于1。可认为抛秧与插秧田中稻水象甲幼虫在任何密度下均呈聚集分布,聚集强度与密度呈正相关。
2.1.4 聚集原因分析根据Taylor幂指数法则测定结果可知,抛秧与插秧2种移栽方式下稻水象甲幼虫在田间均呈聚集分布,聚集的原因因密度不同而异。根据Blackith种群聚集均数λ=mγ/2k检验[3],其中γ为自由度等于2k时的分布函数值,k为负二项分布参数值。当λ≥2时,聚集原因是由昆虫行为或环境因素引起;当λ<2时,聚集原因可能是环境作用引起。根据表 1中抛秧田与插秧田稻水象甲幼虫平均密度m与聚集均数λ,求得两者的线性回归方程分别为:λ1=0.921m1-0.398(R=0.996 5**)(抛秧田); λ2=0.957m2-1.216(R=0.998 0**)(插秧田)。当抛秧田单位样方内的幼虫数小于2.60头(λ1<2),插秧田单位样方幼虫数小于3.36头(λ2<2)时,说明在幼虫密度较低的条件下,稻水象甲幼虫在水稻田的聚集原因与田块的环境有关;当抛秧田与插秧田的单位样方幼虫密度分别大于2.60、3.36头时,即λ≥2,稻水象甲幼虫的聚集原因可能与该田块的环境因素以及昆虫本身聚集习性共同影响有关。本试验所调查的抛秧田与插秧田,其聚集均数λ均大于2,因此,聚集原因为稻水象甲幼虫本身特性及环境因素共同引起。
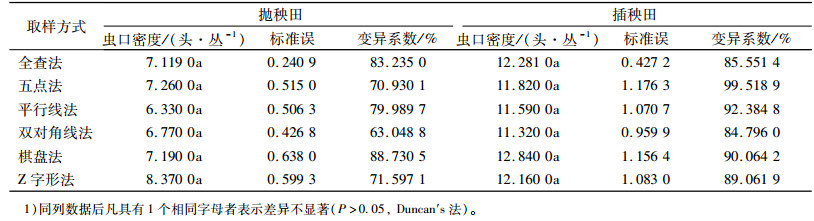
2.2 2种移栽方式下幼虫的抽样调查技术 2.2.1 抽样方法比较将调查结果绘制成坐标图,分别采用五点法、平行线式、双对角线式、棋盘法和Z字形取样法抽取同样的样本数比较各方法的平均数标准误及变异系数,结果见表 2。对5种调查方法测定结果用邓肯氏新复极差法进行差异显著性分析,结果表明五点法、平行线式、双对角线式、棋盘法和Z字形取样法下, 抛秧和插秧2种移栽方式下稻水象甲幼虫的田间调查虫口密度差异不显著,接近田间实际情况(全查法),田间调查时可采用其中任何一种调查方法。在田间稻水象甲幼虫系统调查中,无论是抛秧田还是插秧田,变异系数均以双对角线法最小,分别为63.048 8%和84.796 0%,综合考虑田间调查的操作性以及5种抽样方法中的平均数标准误和变异系数,均以双对角线取样法为最佳取样方式。
|
|
表 2 稻水象甲幼虫不同调查取样方式的准确度比较1) Table 2 A comparison of accuracies of different sampling methods of Lissorhoptrus oryzophilus larvae |
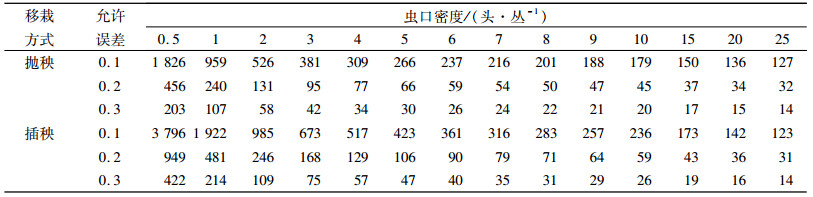
由于Iwao回归模型中的平均拥挤度m*与平均虫口密度m之间的线性关系显著,将系数α、β代入模型,得稻水象甲幼虫在抛秧田中的最适理论抽样公式为:N=t2(2.256/m+0.240)/D2;插秧田为:N=t2(4.878/m+0.126)/D2。取置信度为95%时的t分布值1.96,假设允许误差D分别为0.1、0.2、0.3,田间理论抽样数随稻水象甲幼虫密度的不同而改变(表 3)。允许误差值一定的情况下,所需抽样数随幼虫平均密度增大而减少。
|
|
表 3 稻水象甲幼虫不同密度条件下的理论抽样数 Table 3 Optimum theoretic samples of Lissorhoptrus oryzophilus larvae under different densities |
种群的空间分布结构是昆虫种群的主要特征之一,对了解昆虫种群的扩散、种群管理及持续控制具有一定的实际意义[3]。本试验分别对抛秧田和插秧田稻水象甲幼虫进行了5次抽样调查,4种聚集指标的测定结果表明,稻水象甲幼虫在抛秧与插秧田中的分布型均为聚集分布,且不受移栽方式的影响,聚集的程度均与密度呈正相关,这与我国东北地区的辽宁[4]、西南地区的贵州[10]稻水象甲幼虫田间分布格局是一致的,原因可能是地理环境的差异对其空间分布的影响不大。抛秧田中幼虫的聚集强度比插秧田小,原因可能是秧田揭膜后,抛秧田秧苗的炼秧时间比插秧田短,仅2~3 d,4月中下旬抛秧田开始移栽;而5月上旬插秧田才陆陆续续移栽,此时正值越冬成虫往大田迁移的高峰期,由于稻水象甲成虫有趋嫩习性,插秧田植株比抛秧田植株幼嫩而对稻水象甲成虫的吸引力更强,致使田间稻水象甲卵和幼虫均多于抛秧田,对幼虫的空间分布影响较大。此外,抛秧比插秧提前10~15 d,此期间抛秧田与插秧田的环境也略有不同。
m*-m线性关系表明,2种移栽方式下稻水象甲幼虫在田间分布为个体群;斜率值β分别为1.240和1.126,均大于1,表明其均呈聚集分布。聚集原因分析表明,无论是抛秧田还是插秧田,其聚集均数λ均大于2,因此,稻水象甲幼虫聚集的原因是由环境因素及稻水象甲幼虫自身特性共同引起。
样方的大小及田间抽样数对统计分析结果影响显著。本试验利用五点法、平行线式、双对角线式、棋盘法和Z字形取样法对调查坐标图进行抽样,结果表明各抽样结果与实际平均密度差异不显著,抛秧和插秧水稻田中,利用双对角线法抽样所得的变异系数均最小,分别为63.048 8%和84.796 0%,综合考虑田间调查的操作性以及5种抽样方法的标准误和变异系数,均以双对角线抽样法为最适宜的调查方法。抛秧田理论抽样模型为N=t2(2.256/m+0.240)/D2; 插秧田为N=t2(4.878/m+0.126)/D2。理论抽样数随抽样允许误差与田间幼虫密度的增大而减小。
广西稻水象甲入侵时间比较短,种群尚未稳定,可能在一定程度上影响了幼虫的空间分布格局。稻水象甲营孤雌生殖,对水稻的危害非常大。本研究明确了稻水象甲幼虫在田间(抛秧与插秧田)的分布规律,可为稻水象甲虫情调查、预测预报和综合防治提供指导。
| [1] |
TINDALL K V, STOUT M J. Use of common weeds of rice as hosts for the rice water weevil (Coleoptera: Curculionidae)[J]. Environ Entomol, 2003, 32(5): 1227-1233. DOI:10.1603/0046-225X-32.5.1227 (  0) 0) |
| [2] |
张锋. 江西省乐平市稻水象甲发生规律研究[D]. 南昌: 江西农业大学, 2013.
(  0) 0) |
| [3] |
宣维健, 杨星科, 刘虹, 等. 稻水象甲卵的空间分布型及抽样技术研究[J]. 昆虫知识, 2002, 39(2): 107-110. DOI:10.3969/j.issn.0452-8255.2002.02.006 (  0) 0) |
| [4] |
田春晖, 赵文生, 赵承德, 等. 稻水象甲的发生规律与防治研究: Ⅱ:稻水象甲种群分布的空间格局及田间抽样技术[J]. 辽宁农业科学, 1996(6): 22-26. (  0) 0) |
| [5] |
黄雅文, 孟威, 白剑宇. 稻水象甲田间分布型及复合抽样技术研究[J]. 辽宁农业科学, 1999(3): 11-13. (  0) 0) |
| [6] |
吕旭健, 方勇军, 夏万青. 稻水象甲种群的分布规律及空间格局和抽样技术研究[J]. 温州农业科技, 1999(4): 22-25. (  0) 0) |
| [7] |
颜仁贤. 稻水象甲幼虫及茧在稻根周围分布规律[J]. 植保技术与推广, 1997, 17(6): 34-35. (  0) 0) |
| [8] |
张锋, 丁俊杰, 朱春福, 等. 江西双季稻区稻水象甲田间分布规律[J]. 生物灾害科学, 2013, 36(1): 9-12. (  0) 0) |
| [9] |
张洪程, 戴其根, 霍中洋, 等. 中国抛秧稻作技术体系及其特征[J]. 中国农业科学, 2008, 41(1): 43-52. DOI:10.3864/j.issn.0578-1752.2008.01.006 (  0) 0) |
| [10] |
峗薇, 杨茂发, 廖启荣, 等. 两种育秧方式下稻水象甲幼虫的空间分布型及其抽样技术[J]. 植物保护学报, 2013, 40(2): 128-132. (  0) 0) |
| [11] |
张孝羲, 翟保平, 牟吉元, 等. 昆虫生态及预测预报[M]. 3版. 北京: 中国农业出版社, 2010: 59-68.
(  0) 0) |
| [12] |
张孝羲, 张跃进. 农作物有害生物预测学[M]. 北京: 中国农业出版社, 2006, 37-49.
(  0) 0) |
| [13] |
张文军. 生态学研究方法[M]. 广州: 中山大学出版社, 2007, 51-53.
(  0) 0) |
| [14] |
林兆里, 徐金汉, 许莉萍. 甘蔗条螟卵空间分布型及其抽样该技术[J]. 植物保护, 2012, 38(3): 59-62. DOI:10.3969/j.issn.0529-1542.2012.03.013 (  0) 0) |
| [15] |
丁岩钦. 昆虫数学生态学[M]. 北京: 科学出版社, 1994, 22-134.
(  0) 0) |
 2016, Vol. 37
2016, Vol. 37