颗粒群悬浮速度的测定,属于气固两相流问题,气固两相流的研究广泛应用于气力输送、农业机械、流化床等领域[1-3],且颗粒系统的研究已成为当前国内外研究的热点[4]。
高连兴等[5]为合理设计花生气力分选和二次脱壳气力输送装置,进行了花生脱壳机脱出物主要成分以及杂质等悬浮速度试验;Gorial等[6]对谷物以及秸秆的悬浮速度和悬浮系数进行了研究;王泽南等[7]对球形颗粒临界速度动力特性进行了仿真;以上学者对不同物料进行了各种流场中的悬浮速度试验,并且对物料输送时流体速度进行了研究,但是运用模拟仿真的方法对颗粒群悬浮速度的测量则鲜有研究。在研究气力播种、输送和种子清选时,种子颗粒群的悬浮速度很重要,而且颗粒群的悬浮速度很难通过试验台测量得出,所以有必要开展种子颗粒群悬浮速度模拟预测方法的研究。本文利用EDEM-CFD耦合[8]的方法模拟颗粒体悬浮速度试验,将模拟结果与PS-20物料漂浮速度试验台测定试验比较,再采用耦合的方法模拟不同体积分数下三七种子的悬浮速度,并通过理论计算进行验证。将颗粒换成大豆和稻谷种子完成上述过程,进行推广验证。
1 材料与方法 1.1 颗粒体建模在离散元颗粒的建模中可采用图像技术[9]、CT扫描技术[10]对物料几何特征进行精准的建模,但是由于农业散粒体物料之间存在很大的差异,且具有复杂的外形轮廓,通常采用圆球颗粒聚集体近似真实物料[11-12]。随机选取100粒三七种子,用精度为0.2 mm的游标卡尺测量种子的长、宽、高,范围分别为5.2~7.2、4.8~6.8、4.0~6.0 mm[13]。
采用EDEM离散元分析软件,对于不同粒径的圆球体进行填充叠加逼近真实种子几何尺寸,在离散元软件EDEM中采用5个圆球体填充叠加建立三七种子模型。
1.2 基本参数试验与参数标定本文选用的种子为云南文山三七种子,含水率(w)为48%~55%。用TMS-PRO型食品物性分析仪对三七种子的力学特性进行测定,得出泊松比和剪切模量;通过坠落碰撞试验测得种子之间的碰撞恢复系数。用离散元分析软件EDEM对滚动摩擦系数进行参数标定,模拟仿真物料堆积试验,并与实际堆积试验进行对比,从而确定滚动摩擦系数。模拟所需参数为泊松比0.4,剪切模量1.3×107 Pa,密度为1 100 kg·m-3,颗粒间恢复系数0.48,颗粒间静摩擦系数0.32,颗粒间滚动摩擦系数0.085。
1.3 接触模型本文仿真模拟颗粒在悬浮流场中的情况,视颗粒为非粘性体,假设颗粒碰撞时发生微小形变,可忽略不计。模拟过程采用Hertz-Mindlin接触力学模型[14-16],将颗粒视为硬球模型,颗粒体之间发生颗粒碰撞,相应的公式如下。
相对速度的法向分量为:
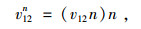
|
切向分量为:
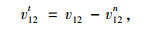
|
两颗粒碰撞后速度为:
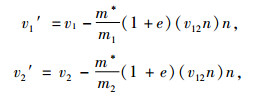
|
式中,v12为颗粒相对速度,n为颗粒发生碰撞时的法向单位矢量, v1, v2分别表示2个颗粒碰撞之前的速度v1′、v2′分别表示2个颗粒碰撞后的速度,t为颗粒发生碰撞时的切向,m*为有效质量,单位矢量m1和m2分别为2个碰撞颗粒的质量,e是恢复系数。
1.4 流场参数PS-20物料漂浮速度试验台测量颗粒悬浮速度的原理是通过出风口处风机的吸力以及叶片的开合角度来控制整个流场的变化。为了模拟此过程,将流场的入口设置为速度入口,将出口设置为自由流量出口, 网格采用结构网格进行划分,选用二阶迎风格式离散对流项,即SIMPLEC算法进行耦合求解。通过计算雷诺数(137 500)得出此流场为湍流流场,为了提高精度,湍流模型选择RNG k-ε模型,并通过计算得出入口处湍流强度为3.65、湍动能为0.20以及湍流耗散率0.93,为模拟流场提供初始数据。
1.5 悬浮速度试验利用PS-20物料漂浮速度试验台(图 1)对三七种子颗粒进行悬浮速度试验,风速用毕托管进行测量,并通过U形管上的液面高差换算得出风速(v)。公式来自试验台说明书。

|
图 1 PS-20物料漂浮速度试验台 Figure 1 PS-20 floating velocity test rig 1:U形管; 2:锥形观察区。 |
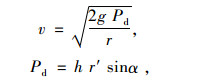
|
式中,g为重力加速度(m·s-2),Pd为压力差(Pa),h为U形管上液压面的差值(m),r′为U形管内所使用的液体容重(kg·m-3),r为在测试环境温度下气体的容重(kg·m-3),α为U形管与水平面的倾角(°)。
气体的容重(r)随温度而变化,设初始状态温度为T0(绝对温度)时的容重为r0,则在温度T时的容重r为:
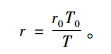
|
利用离散元软件EDEM和计算流体力学软件FLUENT相耦合的方式模拟整个悬浮速度试验,通过试验台测得速度入口的速度为10 m·s-1, 颗粒体随着空气的流动进入流场,整个过程中伴随颗粒体自身转动,这是因为管内横截面各点处的风速不同以及颗粒体投影面积不断变化导致迎风面积改变,使得空气阻力不断变化,致使颗粒体在管内上下翻滚。
1.7 沉降法验证物料悬浮速度与沉降速度在数值上基本相等,但是当颗粒体较多时悬浮速度受到涡流的影响,因此与沉降速度有所不同,采用普拉诺夫斯基修正式[17]来对不同体积分数下的沉降速度进行理论计算作为参照,通过对沉降速度的理论计算对比模拟试验的数据进行验证。雷诺数(Re)计算公式如下:
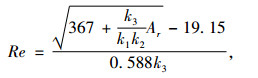
|
式中,k1为颗粒相互作用引起的颗粒运动受约束条件的系数,即颗粒体体积分数的影响系数,k2为由于管壁的影响所引起的颗粒运动受约束条件的系数,k3为颗粒形状影响系数,Ar为阿基米德数。
k1即颗粒群在有限空间内沉降时,颗粒体体积分数(X)对沉降速度的影响:
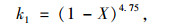
|
k2即管壁对颗粒沉降速度的影响,可用下式表示:
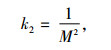
|
式中,M为颗粒体直径和管径之比及与流动状态有关的修正乘积,一般情况下M=1。
k3为颗粒形状修正系数,由于三七种子颗粒为表面不光滑的近球体,所以k3取2.5。
Ar为阿基米德数,其表达式如下:
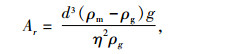
|
式中,d为颗粒体直径,ρm为颗粒密度,ρg为气体密度,η为气体运动黏度。
沉降速度计算公式如下:
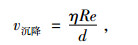
|
式中,η为气体运动黏度,d为颗粒体直径。
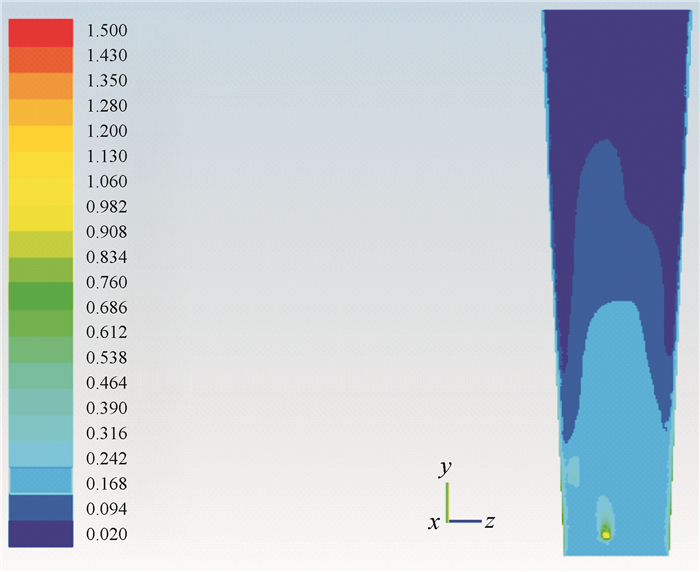
2 结果与分析颗粒体在流场中受到空气流动的作用,同时空气流场也受到颗粒体的影响。图 2为气固耦合流场湍流分布图。如图 2所示,由于颗粒体的存在使得湍流分布出现了变化,明显可以看出,颗粒体位置附近湍动能增强,出现涡体,湍动能随着流体流动逐渐减弱。
|
图 2 气固耦合流场湍流分布图 Figure 2 Distribution nephogram of gas-solid coupling flow field |
颗粒群通过颗粒体积分数进行度量,颗粒体体积分数即所有颗粒体的体积占整个空间体积的百分比。单个三七颗粒体体积平均值为95.46 mm3, 试验台锥形观察筒的体积为3.70×107 mm3。
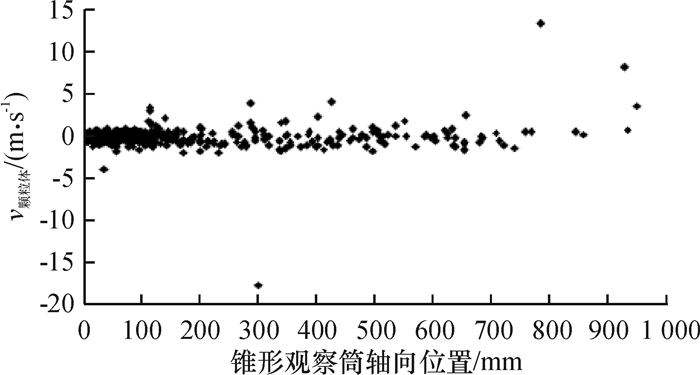
应用EDEM-CFD耦合的方法模拟不同体积分数下的悬浮速度场,设置体积分数为2.58%、3.87%、5.16%。图 3为体积分数为2.58%时颗粒体速度-锥形观察筒轴向位置散点图,多数颗粒体速度在0 m·s-1左右,处于悬浮状态,少数颗粒体由于受到涡流的影响,速度波动比较大。总体上看,此时颗粒体处于悬浮稳定状态。
|
图 3 体积分数为2.58%时颗粒体的速度-锥形观察筒轴向位置散点图 Figure 3 Velocity-position scatter diagram of particles at the volume fraction of 2.58% |
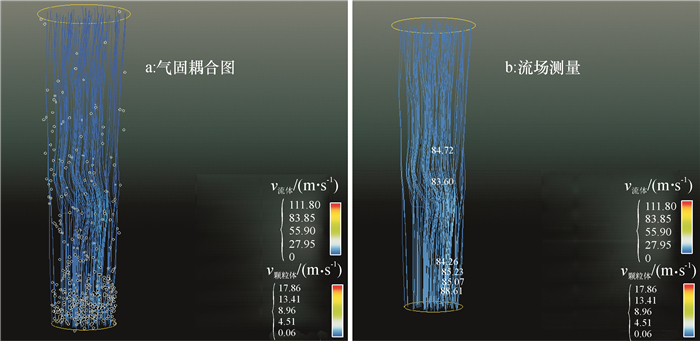
利用ENGSIGHT处理软件进行气固耦合流场的分析。图 4为气固耦合流线场分布图,如图 4a所示,颗粒体充斥于整个管内,多数处于入口附近,流线中段呈现明显弯曲。如图 4b所示,在颗粒体基本处于稳定的情况下,在管内不同的位置,即入口处、底部、中段等颗粒较为集中的地方添加6个软件中的探针来测量此时的流速,其流速范围为8.36~8.86 m·s-1,得出体积分数为2.58%时,平均悬浮速度为8.52 m·s-1。同样的方式对体积分数为3.87%、5.16%、7.74%进行模拟,得出其平均悬浮速度分别为8.72、8.96、9.46 m·s-1。
|
图 4 气固耦合流线场分布图 Figure 4 Distribution of the gas-solid coupling streamiline field |
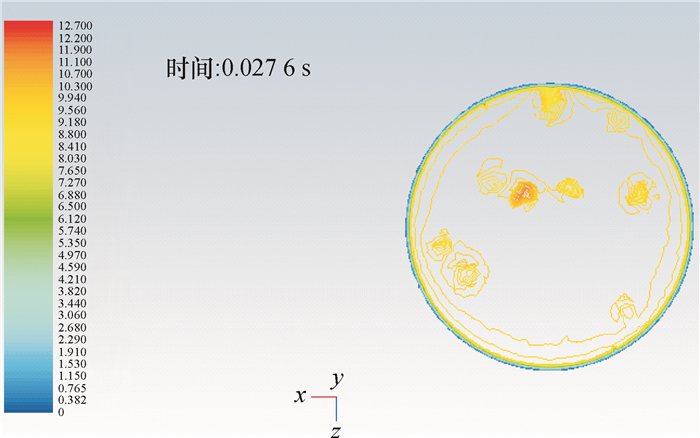
选取体积分数为3.87%时锥形观察筒的一个横截面,图 5为气固耦合流场速度等值曲线分布图,颗粒体周围的空气流速出现明显的变化,靠近颗粒体表面一层流速最大,随着流体远离颗粒体表面,流体流速逐渐减小。
|
图 5 气固耦合流场速度等值曲线分布图 Figure 5 Velocity contour curve profile of gas-solid coupling flow field |
在有颗粒体存在的流场中,当流体流到颗粒体周围,由于颗粒体的存在,出现了涡体,这是因为流体本身具有黏性,当流过颗粒体时边界层分离,形成了尾迹,尾迹随着逐渐运动形成了涡体。
由于颗粒体的存在,加剧了流场的湍流效果,使得流场的运动发生了变化。随着颗粒体增多,流场内湍流效果进一步加剧,存在大量绕流运动,形成涡流。颗粒体受到相间曳力、流体阻力、自身重力,流体间则存在较强的惯性阻力。
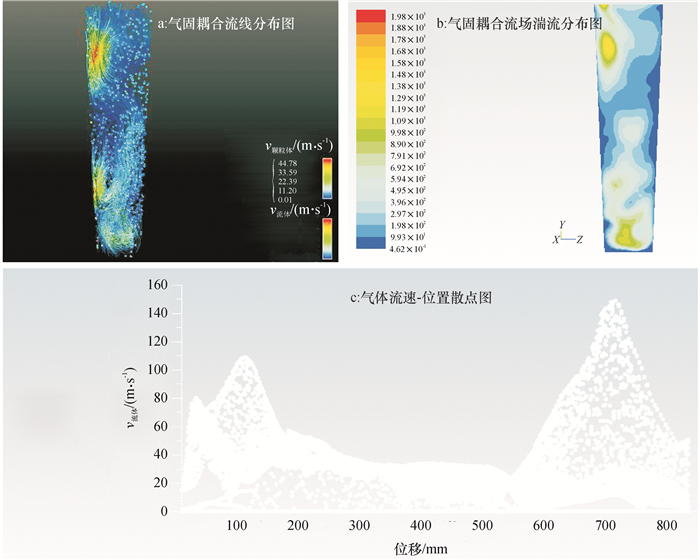
经反复模拟后可知,当体积分数达到9.03%时产生较大涡流。图 6为体积分数为9.03%时流场情况,图 6a为气固耦合流线分布图,可以明显看出流场中产生涡流,图 6b为气固耦合流场湍流分布图,可以看出湍动能在涡流处增强,图 6c可以看出在入口处和出口处产生涡流,涡流处产生较大速度梯度。
|
图 6 体积分数为9.03%时气固耦合流场 Figure 6 Gas-solid coupling flow fields with the volume fraction of 9.03% |
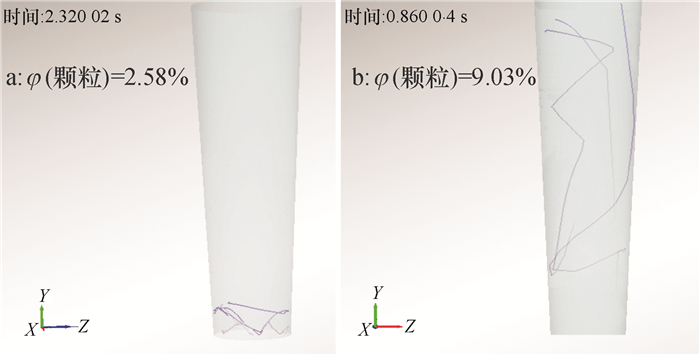
颗粒群体积分数的不同对流场产生不同的影响,反之,流场的不同也将影响颗粒体的运动轨迹,气固之间是一种相互影响、相互作用的过程。图 7为颗粒体的运动轨迹图,图 7a为体积分数为2.58%时的轨迹图;图 7b为体积分数为9.03%时颗粒体的运动轨迹图。明显可以看出,当体积分数为2.58%时,颗粒体对流场影响不大,使得流场未产生大涡流,颗粒处于上下翻滚的悬浮状态,而当体积分数达到9.03%时,由于颗粒体对流场的影响,产生了大涡流,导致颗粒体出现不规则的运动,且与壁面和其他颗粒产生碰撞。
|
图 7 颗粒体运动轨迹图 Figure 7 Diagram of particle trajectory |
三七种子颗粒群体积分数小于9.03%的情况下,流场处于相对稳定的状态,并未出现湍动能与流速大幅度的变化,但随着体积分数的增加,模拟结果与理论计算值的偏差略有增大。这是由于模拟方法考虑到实时因颗粒群体积分数的变化对流场产生的影响,而理论计算方法无法对此种影响进行准确计算。当体积分数达到9.03%之后,由于大量颗粒体的存在,对流场内气体的流动产生了强烈的影响,湍动能产生较大变化,并且伴随着大涡流的形成,颗粒体出现不规则运动。
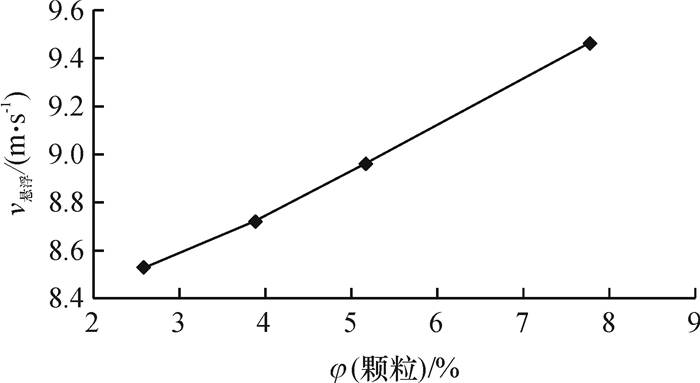
根据上述测得的悬浮速度与体积分数的关系,绘制成散点图(图 8)。为了得到悬浮速度v悬浮与体积分数(x)之间的关系式,本文采用多项式拟合曲线链接散点,得到回归方程如下:
|
图 8 悬浮速度与体积分数拟合图 Figure 8 Fitting of suspension velocity and volume fraction |
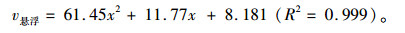
|
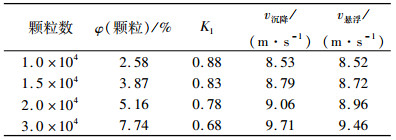
三七种子沉降法理论计算与模拟试验对比结果见表 1。由表 1可以看出,沉降速度计算值与悬浮速度模拟试验值偏差较小,此模拟方法具有一定的可靠性。
|
|
表 1 沉降速度与悬浮速度对比表 Table 1 Comparison between settling velocity and suspension velocity |
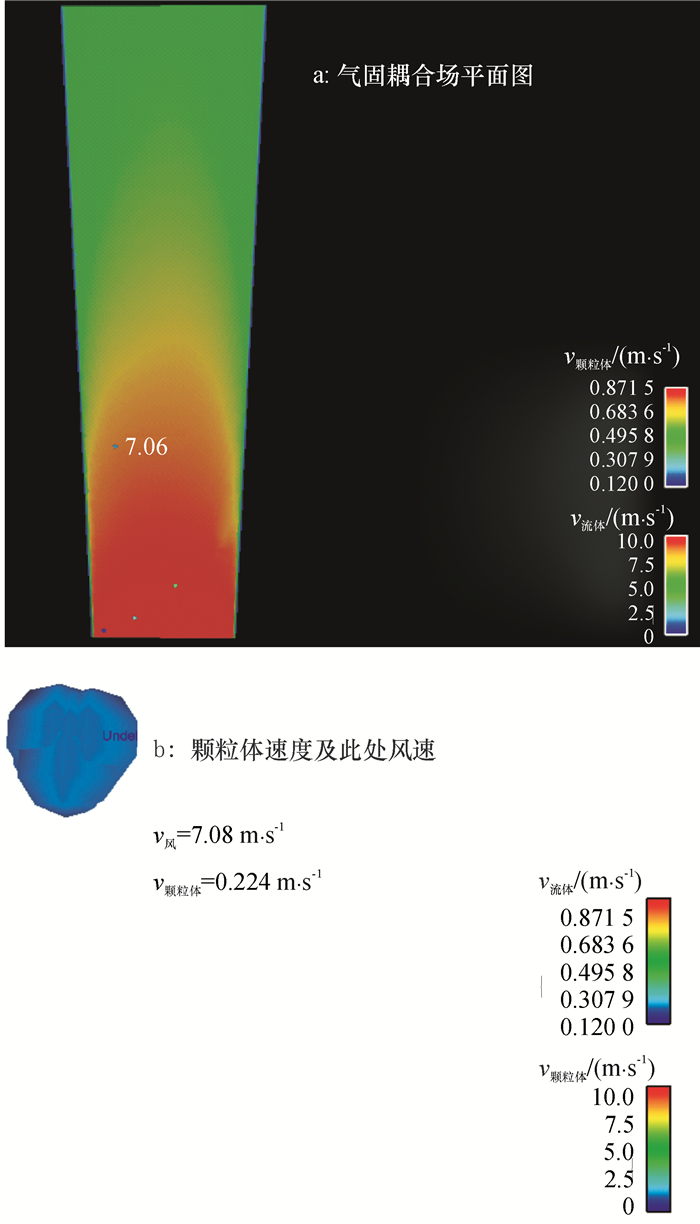
由于试验台的局限性,试验时测量较少三七颗粒,即颗粒体积分数基本为0的情况,图 9为0.2 s时三七颗粒悬浮速度流场,图 9a为利用探针测量出颗粒随空气流动到上浮极限位置时的风速,风速为7.08 m·s-1。图 9b为局部放大图,在风速为7.08 m·s-1时,颗粒体速度为0.224 m·s-1,此时颗粒体有向水平方向运动的趋势,竖直方向速度分量几乎为0。此处的风速为悬浮速度最小风速。
|
图 9 0.2 s时颗粒悬浮速度流场 Figure 9 Particle suspension velocity field at 0.2 s |
同理可测得0.5 s时三七颗粒体悬浮速度流场,风速为9.30 m·s-1时,颗粒体速度为0.015 6 m·s-1。此时颗粒体基本处于静止状态。此处的风速即悬浮速度为最大风速。
利用PS-20物料漂浮速度试验台对三七种子颗粒进行悬浮速度试验,得到悬浮速度范围为7.14~9.32 m·s-1,上述模拟试验结果为7.08~9.30 m·s-1,基本与试验相一致,充分说明了这种模拟方法的准确性和可行性。
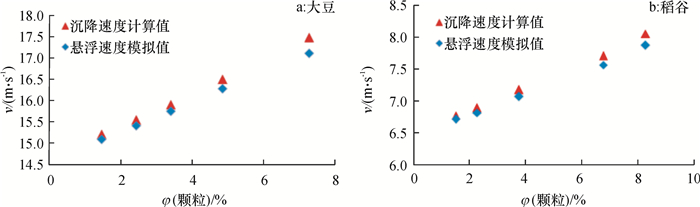
3.3 方法有效性的验证为了验证方法的有效性和推广性,将三七种子分别替换为大豆和稻谷,同样采用上述方法进行试验、计算和模拟。通过试验测得大豆颗粒体的悬浮速度平均值为14.70 m·s-1,模拟结果为14.66 m·s-1;试验测得稻谷颗粒体的悬浮速度平均值为6.55 m·s-1,模拟值为6.52 m·s-1。可见模拟值与试验结果基本一致,为了进一步说明此方法的可行性,分别模拟大豆和稻谷不同体积分数下颗粒群的悬浮速度并与理论计算相对比(图 10),从图 10中可以看出模拟值与理论计算值基本一致,但随着体积分数的增加,模拟结果与理论计算值的偏差略有增大。这是由于模拟方法考虑到实时因颗粒群体积分数的变化对流场产生的影响,反映流场的动态变化,2组试验的最大偏差分别为2.4%、2.2%。结论与上述试验结论基本一致,证明了此方法的有效性和可推广性。
|
图 10 大豆和稻谷模拟试验与理论计算对比 Figure 10 Soybean and rice simulation test and theoretical calculation contrast figure |
1) 利用EDEM-CFD耦合方法模拟颗粒体悬浮速度试验,其结果与实际试验结果相一致,表明此种方法具有很好的适用性。
2) 利用EDEM-CFD耦合的方法模拟颗粒群的悬浮速度,得出三七种子颗粒体积分数为3.87%、5.16%、7.74%时其平均悬浮速度分别为8.72、8.96、9.46 m·s-1,与理论计算值基本一致。采用大豆与稻谷进行验证,得出2组模拟值与理论计算值的最大偏差分别为2.4%、2.2%,说明此方法有效。
3) 三七种子颗粒群体积分数小于9.03%的情况下,流场处于相对稳定的状态,并未出现湍动能与流速大幅度的变化,但随着体积分数的增加,模拟结果与理论计算值的偏差略有增大。当体积分数达到9.03%,流场内气体的流动产生了强烈的变化,湍动能产生较大变化,并且伴随着大涡流的形成,颗粒体出现不规则运动。此方法可以对未出现大涡流情况下不同体积分数下颗粒群的悬浮速度进行模拟预测。
本文的方法为两相流动的研究提供了一种直观、可靠的研究方法,弥补了因PS-20物料漂浮速度试验台仅可以对颗粒体或较少数目的颗粒体进行悬浮速度测量,而对颗粒群的悬浮速度很难进行测量的不足,且可以广泛地应用于不同种类散粒体的研究,但是当颗粒体体积分数过大时,出现大涡流情况,颗粒运动复杂、不规律,无法通过试验、理论计算、模拟等方法得到可靠数据,具有一定的局限性,因此对于多相流问题,就其本质仍需深入研究。
| [1] |
SHI Q F, YAN X Q, HOU M Y, et al. Experimental study of segregation patterns in binary granular mixtures under vertical vibration[J]. Chinese Sci Bull, 2003, 48(7): 627-629. (  0) 0) |
| [2] |
季顺迎. 非均匀颗粒材料的类固-液相变行为及本构方程[J]. 力学学报, 2007, 39(2): 223-237. (  0) 0) |
| [3] |
GENNES P G. Granular matter:A tentative view[J]. Rev Mod Phys, 1997, 71(2): 374-382. (  0) 0) |
| [4] |
赵永志, 江茂强, 徐平, 等. 颗粒堆内微观力学结构的离散元模拟研究[J]. 物理学报, 2009, 58(3): 1819-1825. DOI:10.3321/j.issn:1000-3290.2009.03.069 (  0) 0) |
| [5] |
高连兴, 张文, 杜鑫, 等. 花生脱壳机脱出物的漂浮系数试验[J]. 农业工程学报, 2012, 28(2): 289-292. DOI:10.3969/j.issn.1002-6819.2012.02.050 (  0) 0) |
| [6] |
GORIAL B Y, O'CALLAGHAN J R. Aerodynamic properties of grain/straw materials[J]. J Agr Eng Res, 1990, 46: 275-290. DOI:10.1016/S0021-8634(05)80132-5 (  0) 0) |
| [7] |
王泽南, 张鹏. 农业物料球形颗粒临界速度动力特性的仿真[J]. 农业工程学报, 2002, 18(4): 14-17. DOI:10.3321/j.issn:1002-6819.2002.04.004 (  0) 0) |
| [8] |
杨杰. 基于DEM的立式干燥机颗粒流仿真模拟研究[D]. 武汉: 华中农业大学, 2012.
(  0) 0) |
| [9] |
周基, 田琼, 芮勇勤, 等. 基于数字图像的沥青混合料离散元几何建模方法[J]. 土木建筑与环境工程, 2012, 34(1): 136-140. (  0) 0) |
| [10] |
杜欣, 曾亚武, 高睿, 等. 基于CT扫描的不规则外形颗粒三维离散元建模[J]. 上海交通大学学报, 2011, 45(5): 711-715. (  0) 0) |
| [11] |
于亚军, 周海玲, 付宏, 等. 基于数字颗粒聚合体的玉米果穗建模方法[J]. 农业工程学报, 2012, 28(8): 167-174. DOI:10.3969/j.issn.1002-6819.2012.08.026 (  0) 0) |
| [12] |
石林榕, 吴建民, 孙伟, 等. 基于离散单元法的水平圆盘式精量排种器排种仿真试验[J]. 农业工程学报, 2014, 30(8): 40-48. DOI:10.3969/j.issn.1002-6819.2014.08.005 (  0) 0) |
| [13] |
任闯, 高筱钧, 苏微, 等. 三七种子的物理机械特性试验[J]. 湖南农业大学学报, 2015, 41(1): 109-112. (  0) 0) |
| [14] |
李洪昌, 李耀明, 唐忠, 等. 基于EDEM的振动筛分数值模拟分析[J]. 农业工程学报, 2011, 27(5): 117-121. DOI:10.3969/j.issn.1002-6819.2011.05.019 (  0) 0) |
| [15] |
陈进, 周韩, 赵湛, 等. 基于EDEM的振动种盘中水稻种群运动规律研究[J]. 农业机械学报, 2011, 42(10): 79-83. (  0) 0) |
| [16] |
胡国明. 颗粒系统的离散元素法分析仿真[M]. 武汉: 武汉理工大学出版社, 2010.
(  0) 0) |
| [17] |
丁德承. 颗粒物料临界速度和沉降速度的工程计算[J]. 硫磷设计与粉体工程, 2009(5): 1-7. DOI:10.3969/j.issn.1009-1904.2009.05.001 (  0) 0) |
 2016, Vol. 37
2016, Vol. 37