2. 西安理工大学 理学院,陕西 西安 710048
2. School of Sciences, Xi'an University of Technology, Xi'an 710048, China
随着时代的发展,用户对产品的关注不再只停留于产品的性能和结构方面,优秀的造型设计也成为用户购买产品的重要指标,农业机械产品也不例外。作为农业机械的重要组成部分,拖拉机在我国农业现代化和机械化进程中有着重要的意义。自拖拉机发明以来,其造型经历了长方体型、曲长方体型、梯形体型和曲梯形体型4个阶段[1],可以看出,随着人们物质文化生活水平提高,审美情趣也在发生改变,对农机产品的造型要求也越来越高[2]。早期拖拉机造型设计中,设计师多从人机工程角度入手,更多考虑用户在操作拖拉机时的生理协调性与舒适性等方面[3]。随着时代发展,在拖拉机产品功能严重同质化的情况下,用户心理方面的因素成为设计师研究的重要内容,这就要求对农机具的造型展开研究[4]。我国大多数农机具生产企业仍以功能作为产品开发的唯一目标,导致农机产品的附加值非常低,无法为企业带来更大的利益,这严重影响了农机产品的发展。目前国际上拖拉机的造型设计正向着系列化、大型化、个性化的方向发展,总体配置紧凑、整体线条流畅、机罩等覆盖件平整光滑、造型美观等都成为评价一辆拖拉机设计是否优秀的重要标准[5]。无论从安全还是美观角度,当前拖拉机的设计中,机体整体基本上由机罩包覆,连以往较为常用的外露照明灯也改为隐藏在机罩内,因此机罩成为了拖拉机造型设计中的重点对象。
从造型设计的角度而言,拖拉机机身可以看做是由若干组曲面拼接而成,且每组曲面需光滑拼接形成完整一体的效果。通常在拖拉机概念设计阶段,设计师会通过制作三维数字模型和真实油泥模型的方式,对机身曲面进行非常细致的调整。在计算机辅助设计系统中,传统Bézier曲线是最早应用于造型设计的工具之一,其具有直观、结构简单、对称、凸包性等优秀属性。然而,传统Bézier曲线的形状仅能依据其控制顶点唯一确定,非均匀有理B样条(NURBS)曲线逐步取代了传统Bézier曲线成为目前设计师使用最广的、用于描述产品造型的数学工具。NURBS是一种专门为计算机三维建模建立的数学描述,可以生成复杂的三维曲线曲面,在工业界使用广泛。但由于NURBS本身将有理式引入了参数曲线,其计算复杂、求积分不方便、求导次数增加等特点又导致其运算量巨大,远远超过代数多项式,且对于一些复杂拓扑结构的形态编辑困难,伴随着CAGD领域中大量新的数学工具出现,图形学领域的学者们提出了带参Bézier[6]、C-Bézier[7-8]、q-Bézier[9]、拟三次Bézier[10]及H-Bézier[11-12]、T-Bézier[13]等各种数学工具。本文以拖拉机造型中最具代表性的机罩为例,提出一种基于CE-Bézier曲面光滑连续拼接的拖拉机造型的设计方法,以期快速产生不同的曲面拼接方式,从而获得大量机罩造型方案。
1 拖拉机机罩造型分析从造型角度分析,由于车轮在拖拉机整体视觉效果上占据较大比例,且属于拖拉机整体造型中的不可变因素,因此在拖拉机机身上的机罩(发动机罩壳)和后轮挡泥板等覆盖件则成为最能体现拖拉机整体造型的部分。以拖拉机机罩造型为例,机罩既可视为一个独立的曲面,又可看做是由多张复杂曲面光滑拼接而成的曲面组,而每张复杂曲面又可以理解为由多个简单曲面拼接组合而成。在现代工业生产中,不同的曲面部件单独加工,然后通过装配形成完整的机罩部件。
本文采用CE-Bézier曲面描述拖拉机机罩上的各组曲面或组成复杂曲面的单张曲面片,通过拖拉机机罩曲面组的光滑拼接,将多个单张CE-Bézier曲面组合形成完整的机罩曲面,最后还可以结合文献[14]中的方法,将照明灯、散热孔等位置的形状通过投影裁剪的方式生成,最终获得完整的机罩造型方案。该方法基于CE-Bézier曲面及其拼接技术,可以通过调整曲面的形状参数迅速编辑修改机罩曲面形状和光滑拼接形式,从而快速获得大量拖拉机机罩的造型方案。
2 CE-Bézier曲面本文采用的CE-Bézier曲面不但具有传统Bézier曲面的变差缩减性、凸包性和仿射不变性等几何性质,且由于其属于代数多项式曲面,其运算量也远远低于其他数学工具,最重要的是其具有优良的形状可调性。
2.1 CE-Bézier曲面的定义CE-Bézier曲面由CE-Bézier曲线构建而成,首先需要对CE-Bézier曲线进行定义。给定4个控制顶点Pi∈Rn(n=2, 3;i=0, 1, 2, 3),对t∈[0, 1]定义曲线:
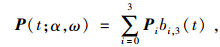
|
(1) |
式中所定义的三次多项式曲线即为含有形状参数α, ω的3次扩展Bézier曲线,简称为CE-Bézier曲线[10]。式中,三次多项式基函数bi, 3(t)(i=0, 1, 2, 3)的定义如下:
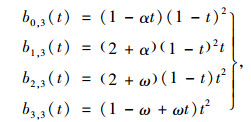
|
(2) |
式中,α, ω∈[-2, 1],称为形状形状控制参数,用以控制曲线线形的细微变化。当α=ω=1时,公式(1)便退化为传统的三次Bézier曲线。
给定4×4个控制网格顶点Pi, j(i, j=0, 1, 2, 3),则CE-Bézier曲线对应的张量积曲面为:
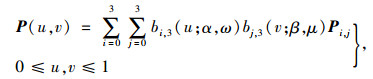
|
(3) |
即[0, 1]×[0, 1]上的CE-Bézier曲面,式(3)中,α, ω, β, μ∈[-2, 1],bi, 3(u),bi, 3(v)则为式(2)中所定义的基函数。
2.2 CE-Bézier曲面的G1连续拼接条件在产品造型设计中,曲面的光滑性是曲面质量优劣的重要指标。优秀的曲线曲面不仅能够使人产生舒适的视觉效果,在实际加工中对于零部件的成型也具有重要作用,因此有必要对曲线曲面的光滑拼接进行分析。实际工程中难以用1张单独的CE-Bézier曲面来表示复杂产品,这就需要采用拼接多张曲面的方法来解决。而且,在制造工程中,曲面间的拼接需达到G1连续才能达到工程制造要求,即需拼接的2张曲面在公共边界处应具有相同的切平面或曲面法线[15-16]。
本文以2张CE-Bézier曲面拼接为例进行阐述。假设需进行拼接的2张CE-Bézier曲面分别为S(u, v; α1, ω1, β1, μ1)与T(u, v; α2, ω2, β2, μ2),两曲面的控制网格顶点分别为si, j(i, j=0, 1, 2, 3)和ti, j(i, j=0, 1, 2, 3),由于CE-Bézier曲面具有u、v 2个方向,因此2张CE-Bézier曲面存在3种方式的拼接:即u-u方向拼接、u-v方向拼接以及v-v方向拼接。本文以u-u方向为例进行阐述。
当2张相邻的CE-Bézier曲面S(u, v; α1, ω1, β1, μ1)与T(u, v; α2, ω2, β2, μ2)满足以下条件且同时成立时:
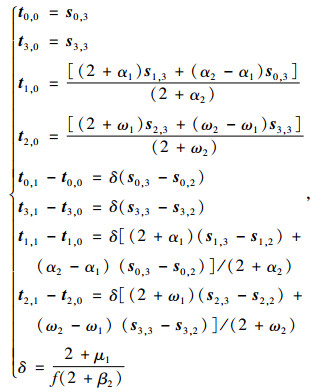
|
(4) |
此时S(u, v; α1, ω1, β1, μ1)与T(u, v; α2, ω2, β2, μ2)在公共边界处达到u-u方向的G1连续拼接。式中,f为大于0的常数。
两曲面在u-v方向以及v-v方向G1连续拼接条件可同理推出。
2.3 CE-Bézier曲面的拼接步骤以CE-Bézier曲面u-u方向的G1拼接为例进行拼接步骤的说明,另外2种方向的拼接方式可同理推出。2张CE-Bézier曲面u方向与u方向G1连续拼接的步骤如下:
步骤1:任意给定一个初始曲面S(u, v; α1, ω1, β1, μ1)的各形状参数α1, ω1, β1, μ1和控制网格顶点si, j。
步骤2:令t0, 0=s0, 3及t3, 0=s3, 3,任意给定形状参数α2和ω2,并根据(4)式中第3与第4等式计算得出t1, 0和t2, 0,此时曲面S(u, v; α1, ω1, β1, μ1)与T(u, v; α2, ω2, β2, μ2)拥有一条相同的公共边界。
步骤3:任意给定形状参数β2和常数f>0,然后在步骤2的基础上根据(4)式第5至第8等式分别计算出曲面T(u, v; α2, ω2, β2, μ2)的第2排控制网格顶点t0, 1,t1, 1,t2, 1和t3, 1。
步骤4:任意给定曲面T(u, v; α2, ω2, β2, μ2)的剩余2排控制网格顶点ti, 2和ti, 3(i=0, 1, 2, 3),形状参数可任意给出,此时,曲面S(u, v; α1, ω1, β1, μ1)与T(u, v; α2, ω2, β2, μ2)已在公共边界处实现G1连续光滑拼接。
在曲面较为复杂的产品造型中,2张曲面的拼接一般无法达到要求,这时,可以反复利用上述步骤进行多张CE-Bézier曲面的光滑拼接。图 1中2张曲面边界处曲面的衔接变化过程和结果可以看出,2张CE-Bézier曲面在公共边界处获得了光滑的过渡效果。
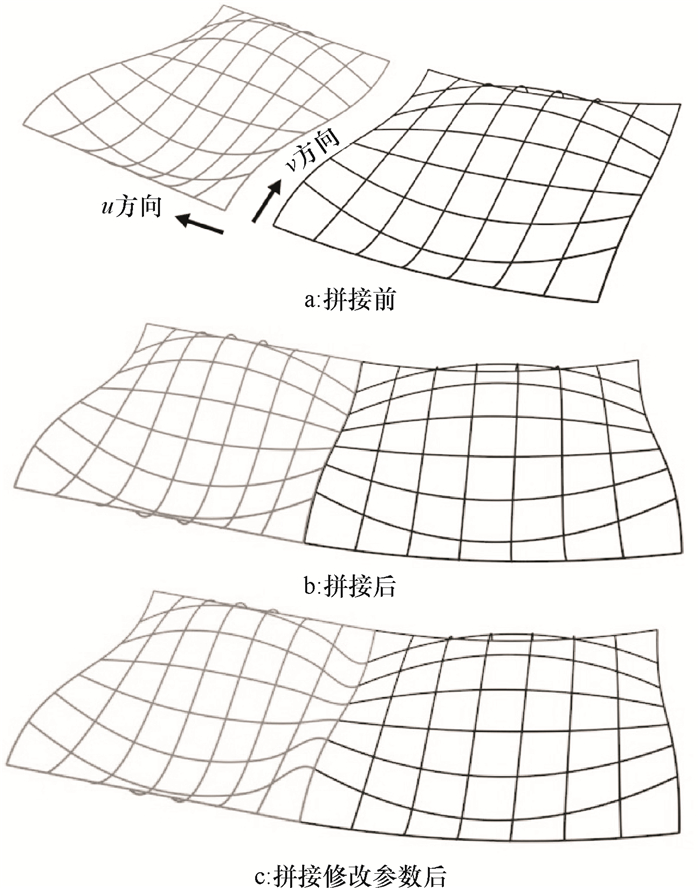
|
图 1 CE-Bézier曲面的G1光滑拼接 Figure 1 G1 continuity between two CE-Bézier surfaces |
另外,由于2张CE-Bézier曲面的形状参数α, ω, β, μ均可任意修改,可在不影响拼接曲面光滑程度的情况下微调曲面形状,十分方便。
通过上述多张CE-Bézier曲面的光滑拼接方式可以看出,进行复杂曲面设计时,设计师可以自由定义初始曲面的形状、多张CE-Bézier曲面拼接时的边界曲线形状与位置,还可以通过改变各曲面形状参数快速获得不同的曲面起伏和拼接结果。因此基于多张CE-Bézier曲面光滑拼接的设计方法具有运算速度快、便于调节形状、能生成大量方案等优点,适合进行各种以曲面为主的产品造型设计。
3 拖拉机机罩曲面的拼接实例作为一种典型的农用机械,拖拉机需适用于不同的使用环境,不同的环境中拖拉机的造型也应有所不同,如在旱地环境中,粘土与沙土土壤要求拖拉机机身各部分的比例不尽相同。平原、山区等环境下拖拉机机身的造型也应有所区别,如轮式和履带式拖拉机因其重心较高大多为曲梯形体型设计,较高的驾驶室还可以保证操作者有宽阔的视野,而2种拖拉机的整体比例又不尽相同;扶手拖拉机则更适合曲长方体型和流线形设计。另外,在造型设计中一方面要使机身色彩与环境协调;一方面要考虑通过美观的拖拉机造型减少操作者的生理、心理疲劳;还要考虑在机身造型上采用大曲面、小曲面等不同的组合方式构成拖拉机整体造型。拖拉机机身可以视为由多张曲面在不同方向拼接而成的复杂曲面,各曲面不同的拼接方式形成了机身的光滑表面或功能线、结构线和装饰线等,如散热罩和排气口处的功能线、形成拖拉机轮廓的结构线和装饰线。本文阐述的类型涵盖各曲面的拼接方式。以拖拉机机罩造型为例,图 2为某拖拉机机罩的原始造型,可以看出右侧部分的复杂曲面造型较为简单,改良空间较大。

|
图 2 原始机罩曲面 Figure 2 The initial hood surface |
图 3示意了机罩侧面利用2张或多张CE-Bézier曲面进行拼接的基本策略,通过调整公共边界曲线位置和参数,可以获得不同的曲面拼接效果,从而获得大量的机罩造型方案,该操作十分便捷,最终拖拉机机罩造型的多种方案结果如图 4所示。
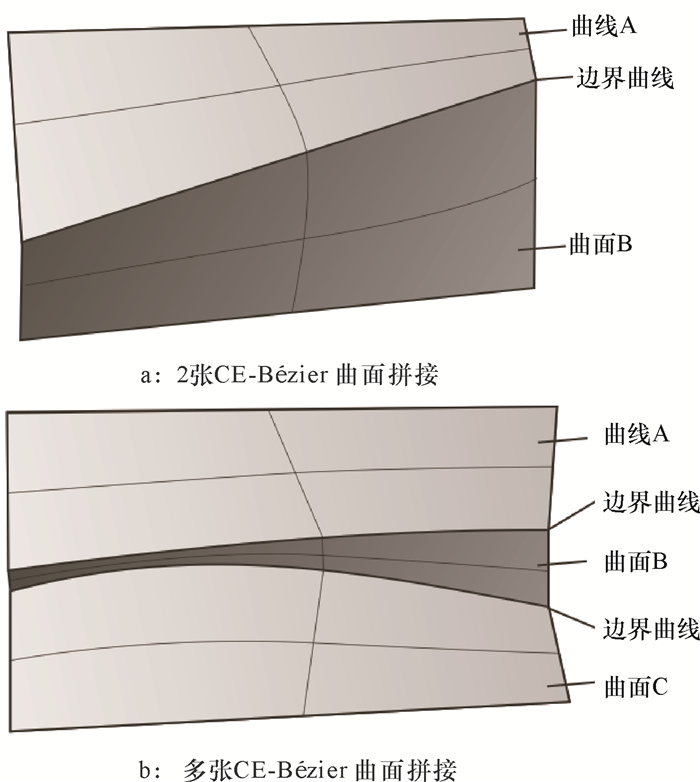
|
图 3 曲面的拼接及方案 Figure 3 The surface blending solutions |

|
图 4 机罩造型方案 Figure 4 Solutions of tractor form design |
与现有CAD系统中的曲面造型工具相比,通过调整CE-Bézier曲面的控制顶点及边界曲线位置与形状参数,可迅速获得大量不同曲面拼接效果,从而得到较多不同风格的拖拉机造型方案。对于拖拉机工业而言,这种方法可以提升拖拉机的造型设计能力,降低开发时间成本,且该方法还适用于以曲面为主的各类工业产品设计,具有很强的可拓展性,能进一步提升设计师的工作效率,具有较好的市场应用前景。
| [1] |
陈为, 陈震邦. 论拖拉机造型的时代性[J]. 农业机械学报, 1995, 26(3): 119-123. (  0) 0) |
| [2] |
曹岩, 肖勇, 张时成, 等. 浅谈拖拉机车身设计[J]. 拖拉机与农用运输车, 2002(3): 40-42. DOI:10.3969/j.issn.1006-0006.2002.03.016 (  0) 0) |
| [3] |
RAJVIR Y, TEWARI V K. Tractor operator workplace design: A review[J]. J Terramechanics, 1998, 35(1): 41-53. DOI:10.1016/S0022-4898(98)00011-1 (  0) 0) |
| [4] |
FUMIHIKO K. Issues in styling and engineering design[J]. CIRP Ann-Manuf Techn, 1997, 46(2): 527-534. DOI:10.1016/S0007-8506(07)60878-6 (  0) 0) |
| [5] |
田玉萍, 王磊. 我国拖拉机产品市场现状及未来发展趋势[J]. 农业技术与装备, 2007, 142(10): 27-29. DOI:10.3969/j.issn.1673-887X.2007.10.016 (  0) 0) |
| [6] |
吴晓勤, 韩旭里. 三次Bézier曲线的扩展Extension of cubic Bézier curve[J]. 工程图学学报, 2005, 26(6): 98-102. DOI:10.3969/j.issn.1003-0158.2005.06.019 (  0) 0) |
| [7] |
ZHANG J W. C-Bézier curves and surfaces[J]. Graph Model Image Process, 1999, 61(1): 2-15. DOI:10.1006/gmip.1999.0490 (  0) 0) |
| [8] |
樊建华, 张纪文, 邬义杰. C-Bézier曲线的形状修改[J]. 软件学报, 2002, 13(11): 2194-2200. (  0) 0) |
| [9] |
ORUC H, PHILLIPS G H. q-Bernstein polynomials and Bézier curves[J]. J Comput Appl Math, 2003, 151(1): 1-12. DOI:10.1016/S0377-0427(02)00733-1 (  0) 0) |
| [10] |
韩西安, 马逸尘, 黄希利. 拟三次Bézier曲线的形状调整[J]. 西安交通大学学报, 2007, 41(8): 903-906. DOI:10.3321/j.issn:0253-987x.2007.08.006 (  0) 0) |
| [11] |
WANG G Z, YANG Q M. Planar cubic hybrid hyperbolic polynomial curve and its shape classification[J]. Prog Nat Sci, 2004, 14(1): 41-46. DOI:10.1080/10020070412331343121 (  0) 0) |
| [12] |
檀结庆, 王燕, 李志明. 三次H-Bézier曲线的分割、拼接及其应用[J]. 计算机辅助设计与图形学学报, 2009, 21(5): 584-588. (  0) 0) |
| [13] |
丁敏, 汪国昭. 基于三角和代数多项式的T-Bézier曲线[J]. 计算机学报, 2004, 27(8): 1021-1026. DOI:10.3321/j.issn:0254-4164.2004.08.003 (  0) 0) |
| [14] |
郭磊, 吉晓民, 胡钢, 等. 基于三次Q-Bézier曲线的车灯造型设计[J]. 中国机械工程, 2013, 24(14): 1961-1969. DOI:10.3969/j.issn.1004-132X.2013.14.023 (  0) 0) |
| [15] |
胡钢, 秦新强, 韩西安, 等. 拟三次Bézier曲线曲面的拼接技术[J]. 西安交通大学学报, 2010, 44(11): 46-50. (  0) 0) |
| [16] |
胡钢, 戴芳, 秦新强, 等. 四次带参Bézier曲线曲面的光滑拼接[J]. 上海交通大学学报, 2010, 44(11): 1481-1485. (  0) 0) |
 2016, Vol. 37
2016, Vol. 37

