荔枝采后分级是其保鲜、包装、销售和深加工前的一个重要工序,能够促进荔枝的优质优价,还能有效提升附加值[1-2]。但荔枝皮薄、肉多,含水量高,常用的滚筒孔框分级法中荔枝频繁翻滚碰撞易产生损伤;而利用三级运动滚筒变换间距实现分级的方法,虽减少了荔枝碰撞损伤,但其分级依据只考虑荔枝个体大小,不够客观全面[3-4]。基于机器视觉的自动分级方法,可减少荔枝损伤,且可依据荔枝外部综合指标快速智能判别分级,更加客观和全面[5]。为实现荔枝的采后自动化快速低损分级,有必要对荔枝无损检测自动分级设备关键技术进行研究。
基于机器视觉的果蔬自动分级设备主要由单体排序输送系统、图像采集与处理系统和分级执行系统组成[6-8]。其中,果蔬实现单体排序输送后,将为后续的分级执行创造有利条件。国内外的学者对单体排序输送机构做了大量研究,Schoot[9]设计了一种斜面提升装置,在单体排序输送的同时实现定向;Ukada[10]设计了一种双锯板交替运动的喂入机构;Font[11]研究了一种用于挤压机的喂入机构,该机构利用链板提升机一次提升多个水果进入单行通道内;Soper等[12]设计了一种双螺旋式单体排序输送机构;刘向东等[13]研究了一种摆杆式单层喂入机构,实现了鲜杏的单体排序输送;左兴健等[14]设计了一种单行排布装置,该装置依靠单行滑板实现了猕猴桃的单个排布输送;赵广华等[15]通过差速法调整不同传输带的速度直至匹配,实现了苹果的单列排序和均匀输送。目前基于机器视觉的荔枝自动分级设备的研究鲜见报道。本研究依据荔枝自动分级设备的工作原理和结构组成,设计其单体排序输送装置,以荔枝卡果次数与空穴率为评价指标,采用单因素和正交试验方法,分析输送装置工作和结构参数对荔枝排序输送效果的影响,寻求较优的参数组合,为提高荔枝单体排序输送效率,开发荔枝自动分级设备提供理论依据和技术参考。
1 材料与方法试验所用荔枝采自广州从化,品种为‘黑叶’,剪去果梗,果实直径为32.0~34.2 mm。
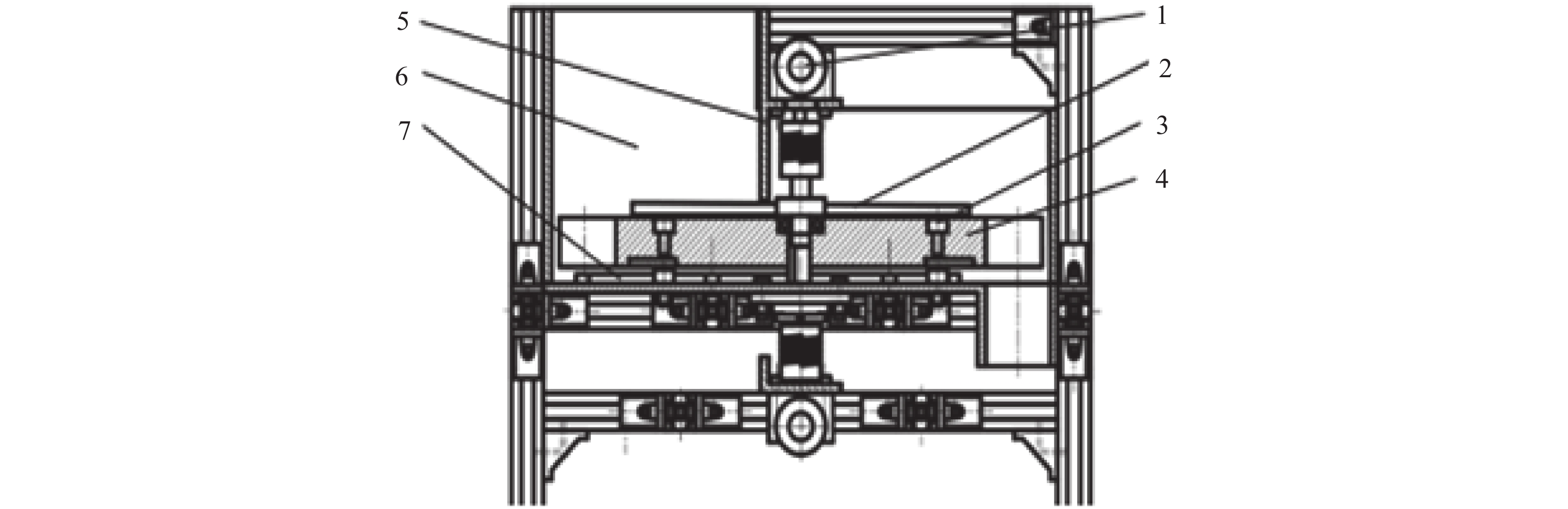
1.1 排序输送装置荔枝单体排序输送装置结构如图1所示,它主要由电机分别控制的上、下转盘构成。上转盘作特定规律的运动,避免荔枝因积聚而产生起拱现象,改善其在圆筒内的流动性;下转盘外缘设有均匀分布的凹坑,其大小恰能安放1颗荔枝;隔板把筒壁内的空间一分为二,一侧放入荔枝,在上下转盘的共同作用下,放入的荔枝逐渐聚集在筒壁附件随下转盘运动自然落入下转盘的凹坑内;进入凹坑的荔枝随着下转盘的转动进入到隔板的另一侧,另一侧的底板上开有1个圆孔,凹坑上的荔枝通过底板上的圆孔落下进入视觉检测区域。通过此装置可实现荔枝的单体排序输送。
|
图 1 双转盘式荔枝单体排序输送装置结构图 Figure 1 The structure of double turnable monomeric delivery device of litchi 1:驱动电机;2:上转盘;3:牛眼轴承;4:下转盘;5:隔板;6:筒壁;7:底板 |
荔枝单体排序输送装置参数优化试验评价指标分别为平均卡果次数和平均空穴率。卡果是指排序输送装置在运行过程中荔枝卡在大转盘与隔板间隙或大转盘与底板孔间隙的现象,发生此现象时必须停机排除干扰,不仅极大地影响运行效率,同时发生卡果后的荔枝易产生损伤;空穴是指荔枝没有按设计要求顺利落入下转盘凹坑的现象,此现象不影响排序输送装置的正常运行但会影响分级的效率。平均卡果次数(η)和平均空穴率(r)计算方法如下:
| $\eta = \frac{1}{n}\left( {{a_1} + {a_2} + \cdots + {a_i}+ \cdots + {a_n}} \right),$ | (1) |
式中,ai(i=1,2···n)为喂入荔枝至完成排序为止发生卡果的次数,n为试验重复次数。
| $r = \frac{1}{n}\left( {\frac{{{b_1}}}{{{m_1}}} + \frac{{{b_2}}}{{{m_2}}} + \frac{{{b_3}}}{{{m_3}}}+ \ldots + \frac{b_i}{m_i}+ \ldots + \frac{{{b_n}}}{{{m_n}}}} \right) \times 100{\text{%}} ,$ | (2) |
式中,bi(i=1,2···n)为喂入荔枝至完成排序为止出现空穴的个数,mi(i=1,2···n)为第i次试验转盘凹坑总数,n为试验重复次数。
1.2.2 试验因素由荔枝单体排序输送装置的工作原理可知,荔枝在装置内的运动主要受到大转盘和小转盘的运动参数影响,此外还受到荔枝间相互作用的影响。由前期试验可知,小转盘设置为变速运动能很好地避免荔枝堆积在隔板与筒壁交接的地方。当小转盘为变速运动时,其运动由运动幅值、运动周期、幅值偏移系数和运动规律共同决定。而大转盘的转速与孔数和荔枝的喂入量会通过影响荔枝的堆积情况进而影响荔枝的排序输送效果。因此参数优化试验选取以下7个试验因素:大转盘转速(A)、小转盘运动幅值(B)、小转盘运动周期(C)、小转盘运动幅值偏移系数(D)、小转盘运动规律(E)、喂入量(F)和大转盘孔数(G)。
1.2.3 单因素预试验首先进行单因素试验,分别考察7个试验因素对荔枝单体排序输送中卡果和空穴情况的影响,各试验因素的水平如表1所示。其中小转盘运动周期和小转盘运动幅值偏移系数由软件设定,为更好地考察其变化关系,分别设置5个水平。每组试验重复5次,每次试验后统计荔枝的卡果次数与空穴率,按公式(1)和(2)计算平均卡果次数和平均空穴率。
|
|
表 1 单因素试验的因素与水平 Table 1 Factors and levels of single factor test |
单因素试验时,大转盘转速确定时,其他试验条件为B2C3D3E2F2G2;小转盘运动幅值确定时,其他试验条件为A2C3D3E2F2G2;小转盘运动周期确定时,其他试验条件为A2B2D3E2F2G2;小转盘运动幅值偏移系数确定时,其他试验条件为A2B2C3E2F2G2;小转盘运动规律确定时,其他试验条件为A2B2C3D3F2G2;喂入量确定时,其他试验条件为A2B2C3D3E2G2;大转盘孔数确定时,其他试验条件为A2B2C3D3E2F2。
1.2.4 正交试验综合考虑单因素试验的结果,采用正交试验法进一步分析各试验因素对荔枝单体排序输送中的卡果和空穴的影响程度,并通过对试验结果的分析比较,获取较优的参数组合。正交试验的因素水平见表2,选用L27(37)正交表进行试验设计,每组试验重复3次。每次试验统计荔枝卡果次数与空穴率,按公式(1)和(2)计算平均卡果次数和平均空穴率。
|
|
表 2 正交试验的因素与水平 Table 2 Factors and levels of orthogonal test |
单因素与正交试验均在荔枝单体排序输送试验台上完成,如图2所示。试验时将荔枝倒入喂料区域,调整好指定的因素水平后,启动开关即可开始试验。

|
图 2 荔枝单体排序输送台 Figure 2 Conveyer table of monomeric delivery device of litchi |
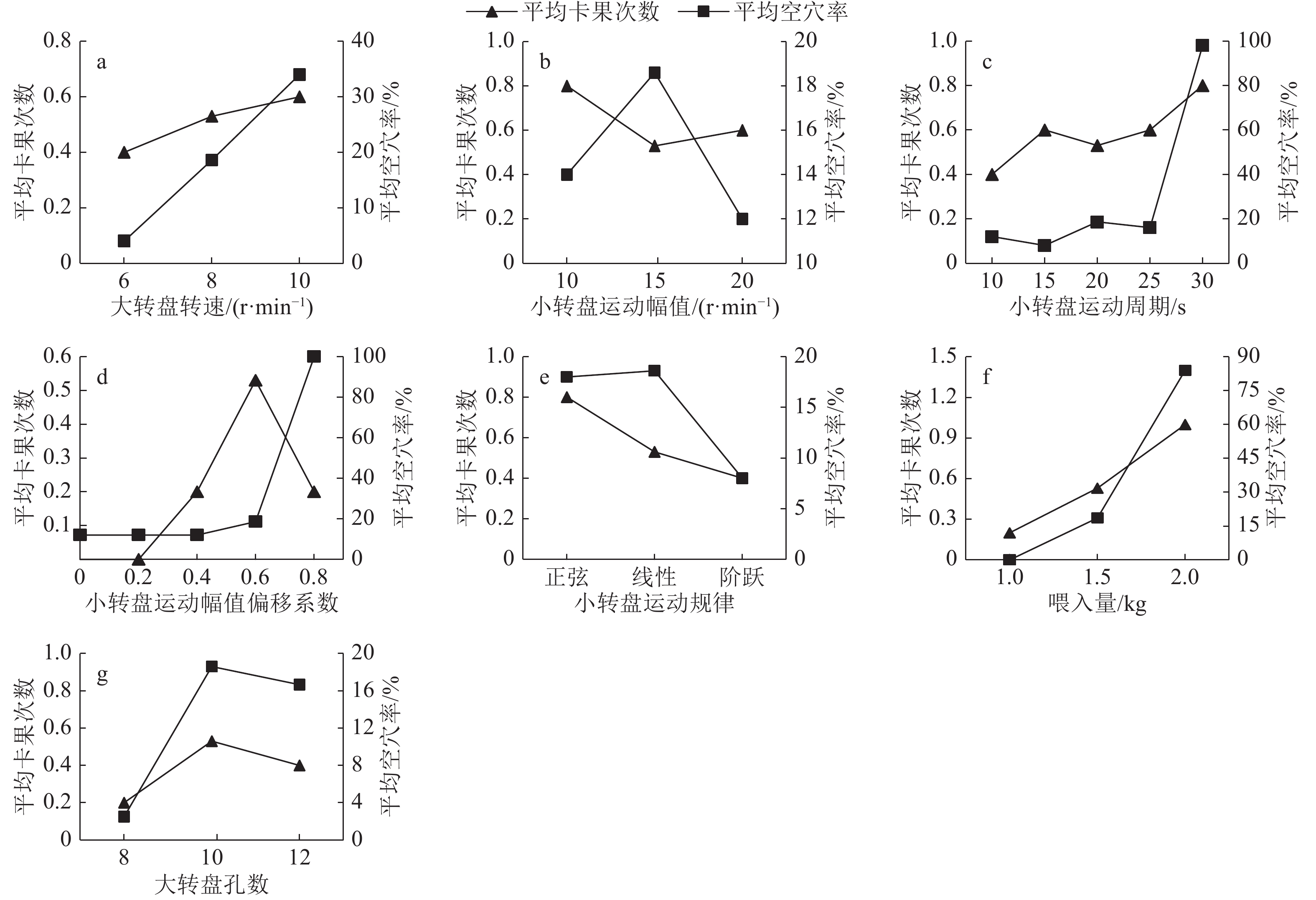
单因素试验结果如图3所示。由图3可见,荔枝卡果次数随着大转盘转速、小转盘运动周期和喂入量的增大而增多,随着小转盘运动幅值的增加先减少后增加,但随着小转盘运动幅值偏移系数和大转盘孔数的增多却先增加后减少;而小转盘运动速度以线性和阶跃方式变化时,卡果次数比较接近。从图3还可看出,平均空穴率随着大转盘转速、小转盘运动幅值偏移系数和喂入量的增加而增大,却随着小转盘运动幅值的增加和大转盘孔数的增多先增加后减少;此外,小转盘运动速度以正弦和线性方式变化时空穴率几乎相同。由以上结果可知,各试验因素对荔枝单体排序输送中的卡果和空穴情况的影响趋势不尽相同。
|
图 3 试验因素对荔枝卡果次数和空穴率的影响 Figure 3 The influence of the test factors on stuck frequency and cavity rate |
正交试验结果及极差分析如表3所示。由表3可见,各试验因素对荔枝卡果次数和空穴率的影响程度是不一样的,影响荔枝卡果次数的最主要因素是喂入量,接着是大转盘转速;而影响荔枝空穴率的最主要因素也是喂入量,接着是小转盘运动幅值偏移系数,其次是大转盘转速。各试验因素对卡果次数的影响顺序为喂入量>大转盘转速>小转盘运动幅值偏移系数≈小转盘运动规律>小转盘运动周期>小转盘运动幅值>大转盘孔数。各试验因素对空穴率的影响顺序为喂入量>小转盘运动幅值偏移系数>大转盘转速>小转盘运动幅值≈小转盘运动规律>小转盘运动周期>大转盘孔数。
根据表3的试验结果,分别可得到以卡果次数和空穴率为评价指标的最优参数组合:A1B3C2D1E2F1G2和A1B2C1D2E2F1G1。显然除试验因素大转盘转速、小转盘运动规律和喂入量外,其余因素的最佳水平选取均不一致。因此需要对2组最优参数进行综合平衡,寻求1组让2个评价指标都比较满意的最优参数组合。
|
|
表 3 正交试验结果及极差分析 Table 3 Orthogonal test results and range analysis |
以卡果次数为评价指标,小转盘运动周期选水平2较好,若以空穴率为评价指标,小转盘运动周期选水平1较好,但小转盘运动周期对卡果次数的影响大于对空穴率的影响,故小转盘运动周期选水平2。
对于小转盘运动幅值偏移系数,若只考虑卡果次数选水平1较好,而考虑空穴率则选水平2较好,但小转盘运动幅值偏移系数对空穴率的影响是主要因素,而对卡果次数的影响接近中间因素,因此小转盘运动幅值偏移系数应该选水平2。
大转盘孔数对2项指标的影响均处于末位,为减少卡果次数,保证机器工作的顺畅,大转盘孔数选择水平2。
通过对各试验参数的综合比较分析,得出综合最优参数组合为A1B2C2D2E2F1G2,即大转盘转速6 r·min–1,小转盘运动幅值为15 r·min–1,小转盘运动周期20 s,小转盘运动幅值偏移系数0.40,小转盘运动规律以线性变化,喂入量1.00 kg,大转盘孔数10个。
2.3 正交试验结果的回归分析通过正交试验得到的单体排序输送装置最优参数组合是基于试验范围内试验因素的水平值。为系统地探究更优的参数组合,进一步对正交试验结果进行回归分析。由于试验因素中,小转盘运动方式是非数值变量,在建立卡果次数(η)和空穴率(r)的回归方程前,需将其转换成虚拟变量并赋值,如表4所示。
|
|
表 4 虚拟变量的设置与赋值 Table 4 Setting and assigning of virtual variables |
根据正交试验及极差分析的结果,建立的卡果次数(η)和空穴率(r)的拟合模型如下,其中各模型均去掉了冗余项。
| $\begin{aligned}\eta = & 0.141x_1+0.019x_2+0.216x_4-0.180x_{5{\rm {a}}}-0.061x_{5{\rm {b}}}-\\ & 2.304x_6+1.071{x_6}^2,\end{aligned}$ |
| $\begin{aligned}r= & 32.5x_1-1.9{x_1}^2+0.8x_2-25.9x_4+52.4{x_4}^2-10.1x_{5{\rm {a}}}-\\& 6.1x_{5{\rm {b}}}-8.2x_6+18.3{x_6}^2-24.8x_7+1.2{x_7}^2,\end{aligned}$ |
式中,x1、x2、x4、x6、x7分别表示大转盘转速、小转盘运动幅值、小转盘运动幅值偏移系数、喂入量和大转盘孔数;x5a、x5b表示小转盘运动规律分别为线性和正弦;模型η和r的P值均小于0.01,决定系数(R2)分别为0.874和0.800,说明卡果次数和空穴率对试验参数的回归方程影响显著。
3 参数优化及验证试验 3.1 基于回归模型的参数优化由于2.2所得的综合最优参数组合A1B2C2D2E2F1G2是基于试验范围内的水平值组合,为得到更优的荔枝单体排序输送效果,对回归非线性模型η和r进行优化,目标是求取其零点。除已定义的虚拟变量外,变量区间为:6 r·min–1≤x1≤10 r·min–1;10 r·min–1≤x2≤20 r·min–1;10 s≤x3≤25 s;0≤x4≤0.80;1 kg≤x6≤2 kg;8≤x7≤12。对于冗余项,即模型η中的小转盘运动周期和大转盘孔数,r中的小转盘运动周期因素,则取单因素试验结果的最优水平。模型η和r求解得到的最优参数组合如下:
模型η:大转盘转速6.55 r·min–1,小转盘运动幅值为12.93 r·min–1,小转盘运动周期10.00 s,小转盘运动幅值偏移系数0.24,小转盘运动规律以正弦变化,喂入量1.20 kg,大转盘孔数8个。模型r:大转盘转速7.00 r·min–1,小转盘运动幅值为15.00 r·min–1,小转盘运动周期17.00 s,小转盘运动幅值偏移系数0.62,小转盘运动规律以正弦变化,喂入量1.10 kg,大转盘孔数8个。
由上述结果可知,模型η和r的求解结果差异较大,即2种指标下的最优参数组合不一致,为寻求同时满足2个评定指标的最优参数组合,定义模型η和r的组合如下,并进行优化求解:
| $\begin{aligned}y=& \eta+\lambda r=0.141x_1+0.019x_2+0.216x_4-0.180x_{5{\rm {a}}}-\\& 0.061x_{5{\rm {b}}}-2.304x_6+1.071{x_6}^{2+}\lambda(0.325x_1-0.019{x_1}^2+ \\ &0.008x_2- 0.259x_4+0.524{x_4}^2-0.101x_{5{\rm {a}}}-0.061x_{5{\rm {b}}}- \\ &0.082x_6+0.183{x_6}^2-0.248x_7+0.012{x_7}^2),\end{aligned}$ |
式中,x1、x2、x4、x6、x7分别表示大转盘转速、小转盘运动幅值、小转盘运动幅值偏移系数、喂入量和大转盘孔数;x5a、x5b表示小转盘运动规律分别为线性和正弦;λ是调整系数(0<λ<1),其意义是以最小化平均卡果次数为主,适当考虑对平均空穴率的影响,从而实现对2个指标的综合优化。模型y求解时与上述设置条件相同,最终得到的最优参数组合为:大转盘转速7.49 r·min–1,小转盘运动幅值为14.14 r·min–1,小转盘运动周期10.00 s,小转盘运动幅值偏移系数为0.33,小转盘运动规律以线性变化,喂入量1.31 kg,大转盘孔数10个,调整系数λ=0.56。
3.2 试验验证为验证参数优化结果的正确性,分别采用基于正交试验水平值的最优参数组合和通过回归模型η、r和y求解得到的最优参数组合在荔枝单体排序输送试验台上进行10次重复验证试验,试验结果如表5所示。由表5可知,η、r和y模型优化结果下的平均卡果次数均优于基于正交试验水平值最优参数组合,而平均空穴率试验值均与基于正交试验水平值最优参数组合下的试验值相近,但y模型的优化结果综合考虑了平均卡果次数和平均空穴率,使得它们的试验值分别降到0和6%,是综合的最优参数组合。
|
|
表 5 参数优化试验结果 Table 5 Experimental results of parameter optimization |
设计荔枝单体排序输送装置,研究其排序输送的效果,分析排序输送装置工作和结构参数对荔枝卡果次数和空穴率的影响,建立回归及组合模型,并对各影响因素进行综合优化,主要结论如下:
1)荔枝卡果次数和空穴率都随着大转盘转速、小转盘运动周期和喂入量的增大而增多,且随着小转盘运动幅值偏移系数的增多,空穴率也增大;但小转盘运动幅值增大,卡果次数是先减少后增加,而空穴率是先增加后减少;此外,卡果次数随着小转盘运动幅值偏移系数和大转盘孔数的增多先增加后减少;小转盘运动以线性和阶跃方式变化时卡果次数比较接近,但空穴率却是小转盘运动速度以正弦和线性方式变化时比较接近。
2)各试验因素对荔枝卡果次数影响重要性排序为喂入量、大转盘转速、小转盘运动幅值偏移系数、小转盘运动规律、小转盘运动周期、小转盘运动幅值和大转盘孔数;对空穴率影响重要性排序为喂入量、小转盘运动幅值偏移系数、大转盘转速、小转盘运动幅值、小转盘运动规律、小转盘运动周期和大转盘孔数。
3)对综合平衡得到的基于正交试验水平值的最优参数组合和回归模型综合求解得到的最优参数组合进行试验分析,得到优化后的荔枝单体排序输送装置参数为大转盘转速7.35 r·min–1,小转盘运动幅值14.30 r·min–1,小转盘运动周期16.93 s,小转盘运动幅值偏移系数0.33,小转盘运动规律以线性变化,喂入量1.31 kg,大转盘孔数10个,此时荔枝卡果0次,空穴率为6%。
| [1] |
张灵光. 农产品质量分级标准是增强市场竞争力的基础[J]. 中国标准化, 2007(10): 59-62. (  0) 0) |
| [2] |
孙宝霞, 汤林越, 何志良, 等. 基于机器视觉的采后荔枝表皮微损伤实时检测[J]. 农业机械学报, 2016, 47(7): 35-41. (  0) 0) |
| [3] |
梁健, 梁材. 荔枝保鲜分级处理工艺及设备[J]. 现代农业装备, 2008(7): 61-63. (  0) 0) |
| [4] |
蒙必胜, 梁兆新, 朱其崇. 链板式间距可调果类分选机的原理及设计[J]. 农产品加工, 2004(8): 35-37. (  0) 0) |
| [5] |
李嘉威, 陈燕, 王佳盛, 等. 荔枝自动分级机的设计研究[J]. 农产品加工, 2017(12): 29-30. (  0) 0) |
| [6] |
王松磊, 刘民法, 何建国, 等. 红枣自动快速无损检测分级机研究[J]. 农业机械学报, 2014, 45(9): 79-83. (  0) 0) |
| [7] |
刘启全. 基于线阵相机的哈密瓜分级机改进设计与试验研究[D]. 乌鲁木齐: 新疆农业大学, 2016.
(  0) 0) |
| [8] |
杜宏伟, 邓立苗, 熊凯, 等. 基于计算机视觉的胡萝卜外观品质分级系统与装备[J]. 农机化研究, 2015, 37(1): 196-200. (  0) 0) |
| [9] |
VAN DER SCHOOT J. Orienting mechanism for orienting fruit, for example: US5078258A[P]. 1992-01-07.
(  0) 0) |
| [10] |
UKADA M. Automatic slope fruit feeding machine used with a fruit grading machine: US5613595A[P]. 1995-04-19.
(  0) 0) |
| [11] |
FONT R O. Fruit feeder for squeezer machines: US5957043[P]. 1982-09-27.
(  0) 0) |
| [12] |
SOPER J L, FREE D R. Screw feeder for proportioning machine: WO1999023019A1[P]. 1999-05-14.
(  0) 0) |
| [13] |
刘向东, 王学农, 王春耀, 等. 鲜杏单体排序间隔输送装置的设计与试验[J]. 农业工程学报, 2016, 32(12): 31-38. (  0) 0) |
| [14] |
左兴健, 武广伟. 猕猴桃自动分级设备设计与试验[J]. 农业机械学报, 2014, 45(S1): 287-295. (  0) 0) |
| [15] |
赵广华, 李鹏飞, 陆奎荣, 等. 智能化苹果品质实时分选系统[J]. 中国科技信息, 2010(19): 123-124. (  0) 0) |
 2018, Vol. 39
2018, Vol. 39


