2. 中国林业科学研究院 资源信息研究所,北京 100091
2. Research Institute of Forest Resource Information Techniques, Chinese Academy of Forestry, Beijing 100091, China
森林生态系统是陆地生态系统的主体,占有80%的陆地碳储量和40%的地下碳储量,是重要的碳库[1-2],在维护全球气候系统、调节全球碳平衡、减缓大气温室气体浓度上升等方面具有不可替代的作用。世界各国越来越重视对以森林生物量为基础的碳汇计量监测[3],国家和区域尺度精准估计森林在乔木生命周期中产生的地上部分和地下部分的生物量、碳储量成为了重要需求[4-6]。近年来,全国范围内已经建立了一些基于林木胸径和树高不同树种的通用性立木生物量模型,然而,由于树木异速生长受到特定立地条件(如树种密度、土壤、光照和地形等)的影响,在具体区域或地块使用通用模型时可能会产生不同程度的误差或不确定性[7-10]。此外,在我国碳汇造林项目实施和计量监测的实际生产中,建立更适合具体区域的单木生物量生长模型,对指导碳汇造林、评价碳汇潜力和分析碳汇动态变化规律,并准确监测和估计碳汇是十分必要的。
森林生物量的估计方法有很多种,回归模型方法可以利用常用的测树因子(如胸径和树高)估算森林中单木和林分以及区域的地上生物量[11]。在树木的生命周期中,各组分(干材、树皮、树枝和树叶)生物量在全株总生物量中的分配会发生变化[7,12-15]。有研究表明,立木生物量的增长随着树木年龄而变化的关系会使以胸径和树高为自变量的模型产生的误差更小[16]。然而,由于树木年龄(特别是天然林)在森林调查中较难获得,很少有研究关注生物量随立木年龄的变化趋势。对于人工林,特别是我国大量的碳汇造林而言,由于其年龄能准确判断,所以可以利用生物量与年龄建立的关系比较准确和直接地获取森林生物量或碳储量及其变化趋势,为森林碳汇交易提供便捷和可靠的依据。因此,探索碳汇造林树种各组分生物量的异速分配,建立以立木年龄为变量的生物量生长模型,具有现实意义。为了研究森林立木各组分生物量随着年龄的变化分布,需要了解树干、树冠的生物量以及占总量的比例,在地上生物量估计的基础上,进一步对干材、树皮、树枝、树叶等各项分量进行估计是十分必要的[17]。在构建地上总生物量模型和各分项生物量模型时,地上生物量总量必须满足同各分项之和相等,因此,构建地上各分量单木生物量相容性模型也一直为林业工作者所重视[18]。
此外,立木地下生物量生长数据仍然缺乏。由于树根难以挖取,很少有研究关注地下生物量变化[6,19]。树根中的地下生物量占森林总生物量的很大一部分,是森林的另一个重要碳库,准确估计树木根系生物量也是乔木生物量估计的重要工作[5,16,20-21]。树根生物量通常采用根茎比方法进行估计,这种方法具有物种和生物学特性[20]。树木生物量各组分在生命周期中的异速生长变化也可能影响根系生物量和生物量根茎比方程。因此,建立立木地下生物量增长随年龄变化的关系,也是精准估计立木生物量及碳汇潜力的需求。
本研究的目的主要有以下2个方面:1)建立生物量随立木年龄变化(以立木年龄为自变量)的地上和地下生物量生长模型;2)建立地上生物量各组分(干材、树皮、树枝和树叶)随立木年龄变化的相容性生长模型。本研究以广东省域3个主要乡土阔叶树种为例,通过实测伐倒木地上、地下部分及地上各组分生物量和树干解析木年轮数据,建立立木生物量随年龄变化的关系,以期为估计森林生物量和碳储量年变化规律提供理论支撑和技术支持。
1 材料与方法 1.1 研究区概况广东省地处中国大陆最南部(20°13′~25°31′N,109°39′~117°19′E)。全省陆地面积17.98万km2,其中,林地10.87万km2。北依南岭,南濒南海,地势北高南低,形成北部山地、中部丘陵、南部平原台地为主的地貌格局,地带性土壤为红壤、赤红壤和砖红壤。广东省属于东亚季风区,从北向南分别为中亚热带、南亚热带和热带气候,降水充沛,年平均降水量1 300~2 500 mm,年平均气温22.3 ℃。樟树Cinnamomum camphora、木荷Schima superba、枫香Liquidambar formosana等,既是广东山地植被中重要的建群树种,也是主要碳汇造林工程项目树种。
1.2 数据采集 1.2.1 单木生物量建模数据建模样本数据来自2013及2016年的广东省樟树、木荷、枫香3个树种的采样和解析木数据。每个树种采伐90株样木,3个树种共270株。每个树种取样按2、4、6、8、12、16、20、26、32和38 cm及以上10个径阶均匀分配,样木伐倒前实测胸径(DBH)、地径和冠幅,将样木伐倒后,测量其树干长度(树高H)和活冠长度,分干材、树皮、树枝、树叶称取鲜质量。每个树种按各径阶分配选择40株样木挖取树根,按根茎(主根)、粗根(直径≥10 mm)、细根(直径<10 mm)分别称取鲜质量。分别抽取样品在85 ℃条件下烘干至恒质量,根据样品干、鲜质量比推算样木地上各组分及地下干质量。
3个树种按照起源分为天然林和人工林2类,分别建立生物量生长模型,数据统计结果见表1。
|
|
表 1 3个树种生物量建模数据统计 Table 1 Statistics of biomass modeling data for three tree species |
解析木年龄(T)数据由年轮估测数据和经验估测数据2部分组成。每个树种中选择40株解析木,并按0.3(0号盘)、1.3(1号盘)和3.3 m以上(2号盘)以2 m为长度分段,以此类推直至尾端长度不足2 m但大于1 m时,以1 m加以分段,各取一圆盘,选取0号圆盘按照东西南北4个方向读取年轮,推测解析木年龄。其余样木根据调查种植年限及观测伐桩年轮(0.3 m)推测树木年龄。
1.3 研究方法研究数据采用Office Excel进行处理,并用R软件进行计算,联立方程组计算采用Systemfit包估计模型参数。
1.3.1 以立木年龄为变量的生物量生长模型选择应用广泛的Schumacher生长方程、Chapman-Richards生长方程、Logistic生长方程及Korf生长方程分别建立3个树种地上和地下部分生物量随立木年龄变化的模型,其公式如下:
Schumacher方程:
| $ B = {\alpha _{_1}} {{\rm{e}}^{ - {\alpha _{_2}}/T}} + \varepsilon , $ | (1) |
Chapman-Richards方程:
| $ B = {\beta _{_1}} {(1 - {{\rm{e}}^{ - {\beta _{_2}} \cdot T}})^{{\beta _{_3}}}} + \varepsilon, $ | (2) |
Logistic方程:
| $ B = {\lambda _1}/(1 + {{\rm{e}}^{{\lambda _2} - {\lambda _3} \cdot T}}) + \varepsilon, $ | (3) |
Korf方程:
| $B = {\theta _1} {{\rm{e}}^{ - {\theta _2}/{T^{{\theta _3}}}}} + \varepsilon, $ | (4) |
式中:
把地上总生物量分成干材、树皮、树枝、树叶4个组分,为确保各组分生物量之和等于总生物量,采用非线性联立方程组的总量控制法求解地上各组分生物量[22]。假设干材占地上总生物量的相对比例函数为1,树皮、树枝和树叶占地上总生物量的相对比例函数分别为
| $\left\{ \begin{gathered} {B_1} = \frac{1}{{1 + {g_1}(x) + {g_2}(x) + {g_3}(x)}} \times {g_0}(x), \\ {B_2} = \frac{{{g_1}(x)}}{{1 + {g_1}(x) + {g_2}(x) + {g_3}(x)}} \times {g_0}(x), \\ {B_3} = \frac{{{g_2}(x)}}{{1 + {g_1}(x) + {g_2}(x) + {g_3}(x)}} \times {g_0}(x), \\ {B_4} = \frac{{{g_3}(x)}}{{1 + {g_1}(x) + {g_2}(x) + {g_3}(x)}} \times {g_0}(x), \end{gathered} \right.$ | (5) |
式(5)中,以立木年龄为自变量,则各组分比例函数形式为
由于生物量数据普遍存在异方差性,必须选用适当的权函数进行加权回归估计或者将模型转换为对数形式消除异方差。本文采用加权方法消除模型的异方差性[22]。对于式(1)~(4),采用原函数
| ${\varepsilon ^2} = {\beta _1} {T^{{\beta _2}}},$ | (6) |
则权函数为
为了检验地上、地下生物量生长模型以及地上各组分相容性生物量生长模型的拟合效果,采用估计值的平均偏差(ME)、标准误(SE)、平均预估误差(MPE)、总相对误差(TRE)和调整后决定系数(
| ${\rm{ME}} = \sum\limits_{i = 1}^n {({{\hat y}_i} - {y_i})} /n,$ | (7) |
| ${\rm{SE}} = \sqrt {\sum\limits_{i = 1}^n {{{({{\hat y}_i} - {y_i})}^2}/(n - p)} }, $ | (8) |
| ${\rm{MPE}} = \frac{1}{n}{t_\alpha }({\rm{SE}}/\overline y ) \times 100,$ | (9) |
| ${\rm{TRE}} = \sum\limits_{i = 1}^n {({y_i} - {{\hat y}_i})} /\sum\limits_{i = 1}^n {{{\hat y}_i}} \times 100,$ | (10) |
| ${{R}}_{\rm{adj}}^2 = 1 - \frac{{n - 1}}{{n - p}}\left( {1 - \frac{{\displaystyle\sum\limits_{i = 1}^n {{{({{\hat y}_i} - {y_i})}^2}} }}{{\displaystyle\sum\limits_{i = 1}^n {{{({y_i} - \bar y)}^2}} }}} \right),$ | (11) |
式中:
表2列出了广东省3个主要乡土阔叶树种地上、地下生物量各模型的参数估计结果。Korf方程在本文所提供的样本中均不收敛,因此表格中只列出了Schumacher、Chapman-Richards和Logistic方程的参数估计结果。Shumacher方程的参数
|
|
表 2 以立木年龄为变量的生物量生长模型参数1) Table 2 Parameters of biomass growth models with tree age as the independent variable |
表3是3个树种不同起源的地上、地下生物量Schumacher、Chapman-Richards、Logistic方程参数估计评价结果。通过比较评价指标可以看出,在估计地上生物量时,3个树种在不同起源下的最优方程不同。樟树的天然林和人工林均是Logistic方程最优;木荷天然林中Chapman-Richards方程最优,人工林中Logistic方程最好;枫香天然林中Chapman-Richards方程最优,人工林中Logistic方程最好。再结合参数来看,Logistic方程可以作为3个树种在不同起源下的地上生物量最优方程。此外Chapman-Richards方程在模拟3个树种的地下生物量时无法收敛,Logistic方程在部分地下生物量模型模拟中也无法收敛,在建立地下生物量生长模型时,Shumacher方程的适用性更好。
|
|
表 3 以立木年龄为变量的生物量生长模型评价1) Table 3 Evaluation of biomass growth models with tree age as the independent variable |
3个树种生物量各组分占地上总生物量的比例与立木年龄的关系如图1所示。由图1可以看出,樟树天然林的干材、树枝生物量占地上总生物量的比例随着立木年龄增加而增大,而树皮和树叶的该生物量占比随着立木年龄的增大而减小,樟树人工林与天然林结果相似。木荷天然林和人工林的干材、树皮和树枝生物量所占地上总生物量的比例随着立木年龄的增加而增大,树叶的该生物量占比随着立木年龄的增加而减小。枫香的结果和樟树的相似。由此可见,各组分生物量在立木生长的周期中占地上总生物量的比例是随着立木年龄的增长而不断变化的,各组分所占比例随立木年龄的增长而升高或降低的趋势因树种而异,因此本研究的各组分相容性模型中将干材部分比例看成1。
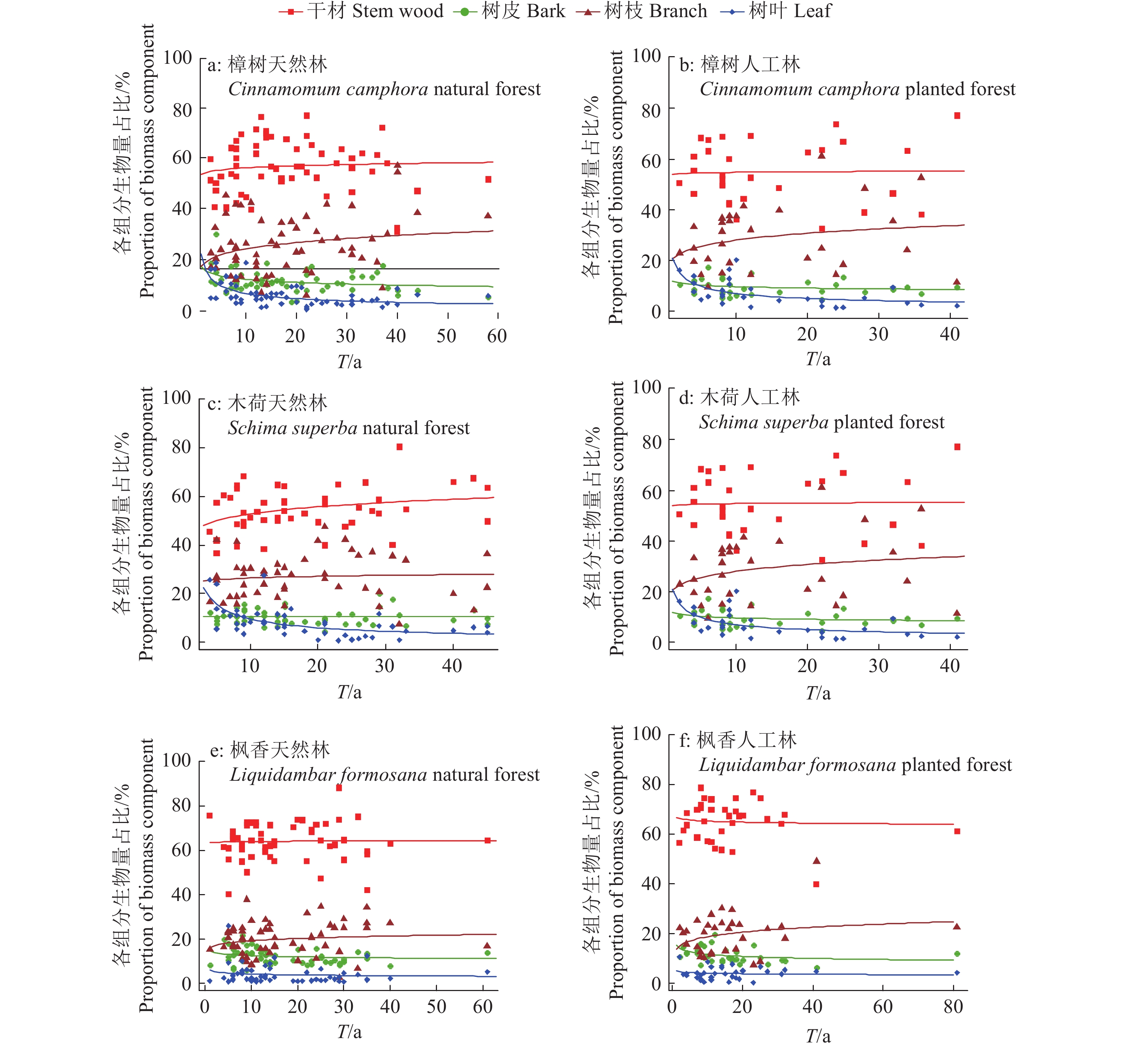
|
图 1 3个树种地上各组分生物量占地上总生物量的比例与立木年龄(T)的关系 Fig. 1 Relationship between the proportion of each aboveground component in total aboveground biomass and the age (T) of three tree species |
选择Logistic方程作为最优方程,采用式(5)拟合的地上各组分生物量生长模型的参数估计结果见表4,各组分方程的评价结果见表5。从各组分评价指标可以看出,干材和树皮的生物量方程拟合效果相对于树枝和树叶更好一些。3个树种干材生物量方程的
|
|
表 4 以立木年龄为自变量的地上各组分生物量相容性生长模型参数1) Table 4 Parameters of the compatibility growth models for biomass of different aboveground components with tree age as the independent variable ×10–2 |
|
|
表 5 以立木年龄为自变量的地上各组分生物量相容性生长模型评价 Table 5 Evaluation of the compatibility growth models for biomass of different aboveground components with tree age as the independent variable |
|
|
表 6 各组分生物量生长模型的权函数估计结果 Table 6 Estimates of weight functions for biomass growth models of different components |
本研究分天然和人工起源建立了广东省域3个主要乡土阔叶树种随年龄变化(以年龄为自变量)的地上、地下生物量生长模型,通过联立方程组建立了地上各组分生物量相容性生长模型。比较了4种模型,包括Shumacher方程、Chapman-Richards方程、Logistic方程及Korf方程的参数及评价指标,得到地上生物量最优模型为Logistic方程,地下生物量最优模型为Shumacher方程。选择Logistic方程对3个树种地上各组分生物量联立方程组建立相容性生长模型,干材和树皮的生物量方程拟合效果相对于树枝和树叶更好。
在天然林或人工林不同起源条件下,相同树种在同一生物量生长模型形式下生物量增长的上限值和最大增速年龄均有差异。通常情况下,人为抚育经营过的人工林的最大增速年龄比天然林小。本文中的木荷样本的地上生物量生长模型估计结果则刚好相反。除了可能的样本取样不够典型以外,由于模型中包含有与林分立地水平和立木密度等条件有关的参数,出现这种现象也是有可能的。因此,也不能确定相同树种、同一模型在不同起源条件下参数估计产生差异的原因是来自起源。曾伟生等[23]曾用非线性混合模型和哑变量模型方法对杉木Cunninghamia lanceolata和马尾松Pinus massoniana,建立了包含林分起源的立木地上生物量和地下生物量模型,认为不同起源的立木地上生物量模型没有明显差异,而地下生物量模型则存在显著差异。在今后的研究中,可以参考利用胸径或树高等表示立木尺寸的因子在相近的立地条件下分起源建立生物量地上、地下及地上各组分其他模型形式的相容性生长模型,以确定起源对3个树种的生长模型影响。
具有相同的立木年龄时,由于立地条件的差异,立木生物量的差异很大。生物量解析木数据的离散程度也会因此变大,相较于以常用的胸径和树高等反映林木大小尺度的因子建立的模型,以立木年龄为自变量的模型的拟合效果和预估效果相对差一些。对于天然林而言,年龄的测定较为复杂费力,胸径和树高仍是建立生物量模型优先选择的自变量。但对于人工林或碳汇造林项目的碳储量估计,由于年龄已知,建立以年龄为自变量的生物量生长模型,则可以省去测量立木尺寸的人力和物力而直接得到估计结果,为估算和监测森林碳汇潜力和碳汇动态的变化提供了便捷的方法。在胸径和树高已知时,首先建立一元和二元立木生物量模型,这是碳汇计量的基础。之后可以利用年龄信息,建立胸径和树高的平均生长模型,供宏观估计平均碳汇潜力提供参考依据[24]。
本研究还讨论了广东省3个主要树种地上、地下生物量及地上生物量各组分所占比例随着立木年龄的变化。本研究的3个树种均为阔叶树,与曾伟生等[22]对马尾松的研究相比,干材的比例随着立木年龄增大变化幅度更小,而马尾松的树枝比例随着胸径的增长表现得更稳定。由于天然林立木年龄测量复杂,很少有研究关注立木年龄对地上各组分在树木生命周期中占全株分配变化的影响。Zavitkovski[25]比较了与文献中不同立木年龄样本建立的方程后,认为年龄会显著影响地上、地下及地上各组分生物量与树木尺寸的关系。Peichl等[16]讨论了4个不同年龄的北美乔松Pinus strobus地上和地下生物量各组分占比的变化情况,认为年龄影响着立木各组分生物量在生长过程中的分配,在不考虑树木年龄的情况下,仅仅考虑以胸径和树高等变量建立的异速模型,在估计不同年龄的样木生物量时误差较大。Sprizza[13]认为在以胸径和胸径–树高为自变量的地上各组分异速生长方程中加入年龄因子可以改善模型的估计效果,减小误差。从广东省3个主要乡土阔叶树种建立的以立木年龄为自变量的生物量生长模型来看,地上生物量各组分在立木生长的周期中占地上总生物量的比例是随着年龄的增长而不断变化的,各组分占比变化的趋势具有树种特异性。在今后的研究中,仍需要根据树种的不同生长特性进一步分析。
| [1] |
DIXON R K, SOLOMON A M, BROWN S, et al. Carbon pools and flux of global forest ecosystems[J]. Science, 1994, 263(5144): 185-190. DOI:10.1126/science.263.5144.185 (  0) 0) |
| [2] |
GOODALE C, APPS M, BIRDSEY R, et al. Forest carbon sinks in the Northern Hemisphere[J]. Ecol Appl, 2002, 12(3): 891-899. DOI:10.1890/1051-0761(2002)012[0891:FCSITN]2.0.CO;2 (  0) 0) |
| [3] |
董利虎, 李凤日, 贾炜玮, 等. 含度量误差的黑龙江省主要树种生物量相容性模型[J]. 应用生态学报, 2011, 22(10): 2653-2661. (  0) 0) |
| [4] |
VOGT K. Carbon budgets of temperate forest ecosystems[J]. Tree Physiol, 1991, 9(1/2): 68-86. (  0) 0) |
| [5] |
KURZ W A, BEUKEMA S J, APPS M J. Estimation of root biomass and dynamics for the carbon budget model of the Canadian forest sector[J]. For Res, 1996, 26(11): 1973-1979. (  0) 0) |
| [6] |
BROWN S. Measuring carbon in forests: Current status and future challenges[J]. Environ Pollut, 2002, 116(3): 363-372. DOI:10.1016/S0269-7491(01)00212-3 (  0) 0) |
| [7] |
SATOO T, MADGWICK H A I. Forest Biomass[M]. Boston: Martinus Nijhoff/Dr. W. Junk Publishers, 1982: 1-152.
(  0) 0) |
| [8] |
WANG J R, LETCHFORD T, COMEAU P, et al. Above- and below-ground biomass and nutrient distribution of a paper birch and subalpine fir mixed-species stand in the Sub-Boreal Spruce zone of British Columbia[J]. For Ecol Manag, 2000, 130(1/2/3): 17-26. (  0) 0) |
| [9] |
LITTON C M, RYAN M G, TINKER D B, et al. Belowground and aboveground biomass in young post fire lodge pole pine forests of contrasting tree density[J]. For Res, 2003, 33(2): 351-363. (  0) 0) |
| [10] |
TATENO R, HISHI T, TAKEDA H. Above- and belowground biomass and net primary production in a cool-temperate deciduous forest in relation to topographical changes in soil nitrogen[J]. For Ecol Manag, 2004, 1936(3): 297-306. (  0) 0) |
| [11] |
赵菡, 雷渊才, 符利勇. 江西省不同立地等级的马尾松林生物量估计和不确定性度量[J]. 林业科学, 2017, 53(8): 81-93. (  0) 0) |
| [12] |
HELMISAARI H S, MAKKONEN K, KELLOMAKI S, et al. Below- and above-ground biomass, production and nitrogen use in Scots pine stands in eastern Finland[J]. For Ecol Manag, 2002, 165(1/2/3): 317-326. (  0) 0) |
| [13] |
SPRIZZA L. Age-related equations for above- and below- ground biomass of a Eucalyptus hybrid in Congo
[J]. For Ecol Manag, 2005, 205(1): 199-214. (  0) 0) |
| [14] |
施文涛, 谢昕云, 刘西军, 等. 安徽大别山区杉木人工林乔木层生物量模型及碳贮量[J]. 长江流域资源与环境, 2015, 24(5): 758-764. (  0) 0) |
| [15] |
刘茂秀, 史军辉, 王新英, 等. 塔河流域天然胡杨林不同林龄地上生物量及碳储量[J]. 水土保持通报, 2016, 36(5): 326-332. (  0) 0) |
| [16] |
PEICHL M, ARAIN M A. Allometry and partitioning of above- and belowground tree biomass in an age-sequence of white pine forests[J]. For Ecol Manag, 2007, 253(1): 68-80. (  0) 0) |
| [17] |
WARING R H, RUNNING S W. Forest ecosystems analysis at multiple scales[M]. 2nd ed. San Diego, California: Academic Press, 1998: 1-431.
(  0) 0) |
| [18] |
符利勇, 雷渊才, 孙伟, 等. 不同林分起源的相容性生物量模型构建[J]. 生态学报, 2014, 34(6): 1461-1470. (  0) 0) |
| [19] |
WANG C. Biomass allometric equations for 10 co-occurring tree species in Chinese temperate forests[J]. For Ecol Manag, 2006, 222(1): 9-16. (  0) 0) |
| [20] |
CAIMS M A, BROWN S, HELMER E H, et al. Root biomass allocation in the world’s upland forests[J]. Oecologia, 1997, 111(1): 1-11. DOI:10.1007/s004420050201 (  0) 0) |
| [21] |
韩畅, 宋敏, 杜虎, 等. 广西不同林龄杉木、马尾松人工林根系生物量及碳储量特征[J]. 生态学报, 2017, 37(7): 2282-2289. (  0) 0) |
| [22] |
曾伟生, 唐守正. 利用度量误差模型方法建立相容性立木生物量方程系统[J]. 林业科学研究, 2010, 23(6): 797-802. (  0) 0) |
| [23] |
曾伟生, 王雪军, 陈振雄, 等. 林分起源对立木生物量模型的影响分析[J]. 林业资源管理, 2014(2): 40-45. (  0) 0) |
| [24] |
刘四海, 曾伟生. 马尾松宏观尺度单木生长模型研究[J]. 林业资源管理, 2017(2): 28-33. (  0) 0) |
| [25] |
ZAVITKOVSKI J. Dry weight and leaf area of aspen trees in the northern Wisconsin[C]// Proceedings of the XV IUFRO Congress on Forest Biomass Studies, IUFRO on Forest Biomass Studies, Section 25, Growth and Yield, March 15-20, University of Florida, Gainsville, Florida, USA, 1971: 191-205.
(  0) 0) |
 2019, Vol. 40
2019, Vol. 40

