我国是农业大国,目前施用农药防治病虫害依然是保证粮食生产的重要手段。小型植保无人机由于操作便捷、成本较低、作业效率高等优点,近年来发展迅速。随着飞控系统的日渐完善,市场对精准施药提出了更高的要求。农用喷头对雾滴要求较高,不同的地块喷施量、雾滴大小适宜范围不同,应针对不同病害状况的田块进行喷施量的调节[1-2]。因此变量喷洒系统的研发是实现精准施药的必要条件。目前,变量喷施控制主要有压力调节式、浓度调节式和PWM间歇喷雾流量调节式3种[3],其中PWM间歇喷雾流量调节最符合精准施药的要求,但其对系统精度要求较高。国外针对PWM间歇喷雾对喷头流量以及喷雾均匀性控制已进行了大量研究[4-6],并有成熟产品面世。国内对变量喷雾技术也有一些研究,王玲等[7]设计了微型无人机脉宽调制型变量喷药系统,并在风洞环境下对悬停状态无人机变量喷施的雾滴沉积规律进行了研究;王浩等[8]以STC12C5410AD单片机为载体,结合机器视觉技术设计了杂草精准变量喷施系统;但国内研究相对而言还不够深入,缺少成熟产品。因此对变量喷施的研究尚不能完全达到要求。
磁流变液,又称磁流体,是智能材料的一种,它既具有液体的流动性又具有固体磁性材料的磁性,在自然状态下它为低黏度的Newton流体,而在磁场作用下,磁流变液会表现出强磁性,黏度增大且流动性迅速降低;当撤去磁场,磁流变液又恢复为可流动的液体[9]。由于磁流变液流变过程是瞬时、可逆的,因此其在材料制造业、工业等领域具有广泛的应用前景[10]。
本研究针对目前航空植保喷头调节流量手段较单一的现状[11-12],利用磁流变液特有的性质,拟设计1种新型农用变量喷头。不同于以往研究着重于控制泵的输出,此研究不对水泵做任何改变,而是在喷头内部添加磁流变液,将磁流变液的特性与传统液力式雾化喷头结构相结合,通过控制磁流变液的固液二相转换对雾化腔内部空间结构产生影响,以达到最终调控流量的目的。
1 磁流变液喷头工作原理及结构设计为达到良好的雾化效果,本研究选择液力式喷头雾化,并在内部添加旋流腔进一步提升雾化效果。当液力式喷头正常工作时,液体受水泵提供的压力影响高速流动,并在旋流腔内高速旋转离心,到达孔径非常狭窄的喷孔时,液体受到剧烈挤压而形成细微雾滴。雾滴离开喷孔后,由于惯性而继续受离心力作用。在这个阶段雾滴表面形成空心的锥形液膜,并逐渐被挤压拉伸形成细丝带状,最后二次破碎成均匀的雾滴[13]。液力喷头的流量调节方式一般通过改变隔膜泵的输出压力实现,但剧烈的压力变化会同时影响到雾滴特性,如压力增大,喷头流量增多,雾滴粒径反而随之减小,最终可能影响到其喷幅以及均匀性等。本研究不对泵压进行改变,考虑对雾化腔的入口开度进行控制,达到流量调节效果。在雾化腔入口处添加磁流变液并加以控制,使其物理状态发生变化,影响到雾化腔空间,实现所需功能。当水泵工作,且线圈电源处于断开状态时,液体进入喷体,通过弹性薄膜与喷体内壁之间的缝隙到达旋流腔,旋转加速后再经由喷孔急剧压缩形成小雾滴喷出;当线圈电源接通,线圈所产生的磁场对弹性薄膜内部的磁流变液产生作用,磁流变液产生磁化,向线圈方向聚集,同时黏度增强,流动性降低,形态由液态向半固体转变。这种变化造成弹性薄膜与喷体内壁的间隙增大,从而使通过此处的液体流速发生改变,最终影响到出口处的流量。
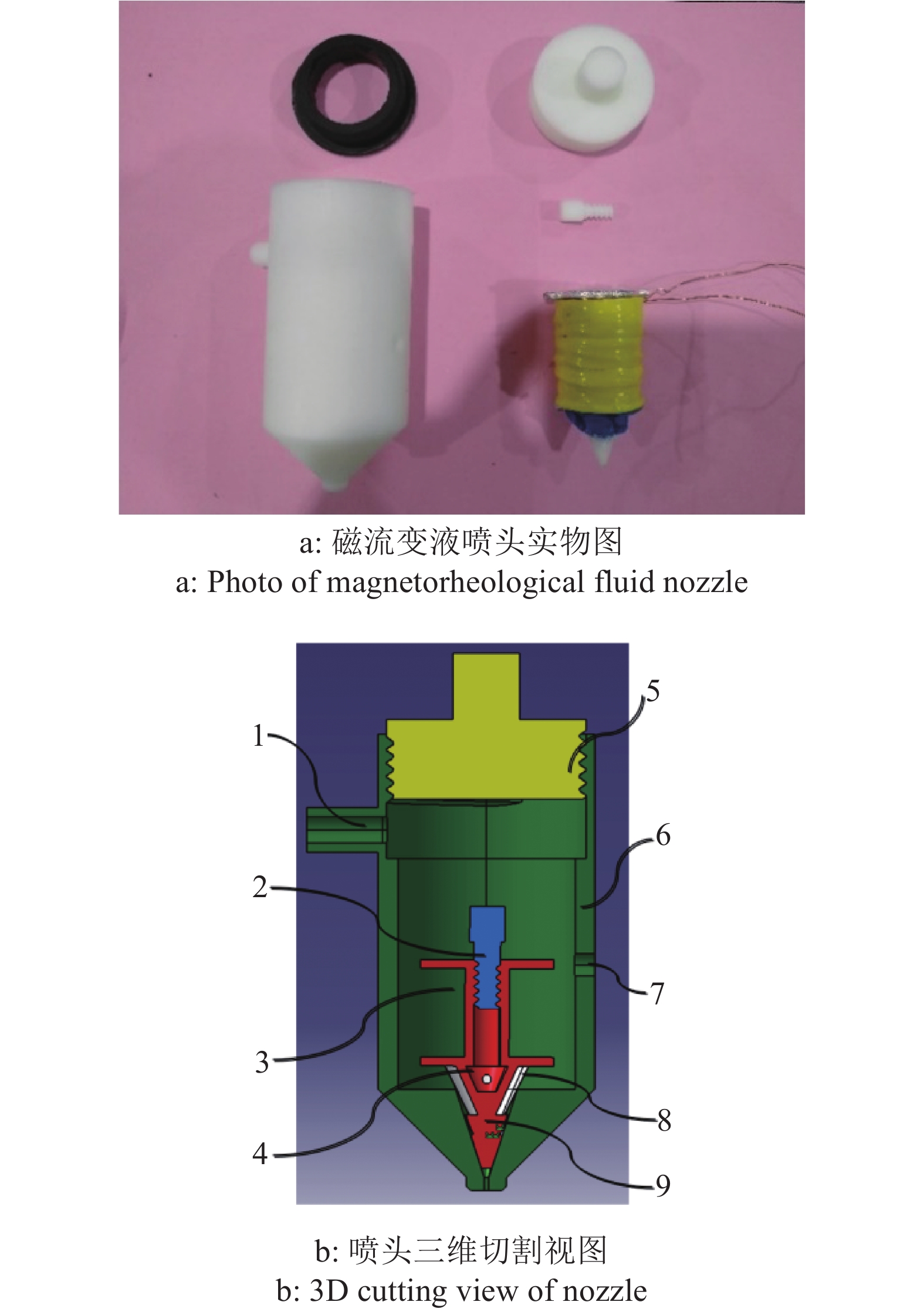
如图1所示,变量喷头主要由入水口、磁流变液腔端盖、线圈绕线轴、磁流变液腔、喷头端盖、外壳体、导线孔、弹性腔、旋流腔等零部件组成。喷头喷体为使液体雾化的主要部件,中部开有通孔用于引出线圈导线,导线引出后在通孔处加注玻璃胶防止滴漏。喷头内部增加了磁流变液与线圈轴结构,因此喷体尺寸相比传统液力喷头较大。根据标准GB/T18687—2012[14],为方便喷头内部不同规格的零部件安装与更换,喷头外壳体直径定为50 mm,喷体高度由内部线圈高度决定。喷体喷孔孔径为决定雾化效果的主要参数,传统航空施药空心圆锥喷嘴的孔径多为0.5~2 mm[15]。本研究重点探究磁流变效应对喷头流量的调控作用,因此只选取1种适合超低容量喷雾的孔径(1 mm)作为参数优选。旋流腔放置在雾化腔内,液体经过旋流槽受离心力作用加速雾化。旋流腔参照常规旋流喷嘴多旋流槽的设计[16-17],采用对称式结构(双旋流槽),以保证流体加速雾化的均匀性。弹性膜可发生弹性形变,包裹在线圈轴下部外侧形成弹性腔,用于承载磁流变液。弹性膜在填充磁流变液后与喷体内壁留有细微间隙供流体通过。线圈轴外侧缠绕有导线构成励磁线圈,其绕制匝数以及线径的选型根据计算及仿真结果确定。线圈内部为中空设计,构成用于承载磁流变液的磁流变液腔;其顶端开有磁流变液注液口,下部斜面开有对称通孔。磁流变液从注液口注入,通过下部通孔到达线圈轴与包裹在外的弹性薄膜所组成的腔体,直到磁流变液注射量达到所需值,封闭注射口。弹性腔与线圈组成了喷头流量控制的关键。
|
图 1 磁流变液喷头 Fig. 1 Magnetorheological fluid nozzle 1:入水口;2:磁流变液腔塞;3:线圈绕线轴;4:磁流变液腔;5:喷头端盖;6:外壳体;7:导线孔;8:弹性腔;9:旋流腔 1:Water inlet;2:Plug of magnetorheological fluid chamber;3:Coil axis;4:Magnetorheological fluid chamber;5:Nozzle lid;6:Nozzle shell;7:Wire guide hole;8:Elastic chamber;9:Swirl chamber |
无磁场作用时,磁流变液内部粒子无规律地自由分布,黏度较小且呈现可流动性。施加磁场后,磁流变液瞬间由Newton流体转变为Bingham流体,其表观黏度显著增大,且随磁场的增大而增大[18]。磁流变液的形态转换发生在毫秒级的时间内,且过程完全可逆。
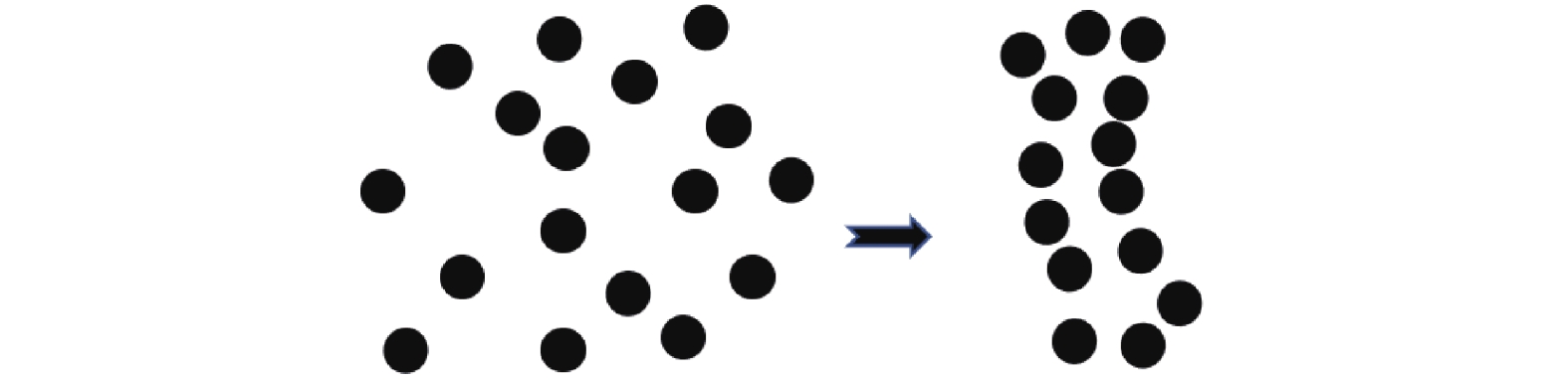
当受到磁场作用时,磁流变液的Bingham流体特性具体表现为:原本随机分布的粒子开始相互快速吸引并沿磁场方向紧密聚集,颗粒间距离变小,形成链状结构且同时产生磁性[19],如图2所示。由于这些链状结构相互聚集,磁流变液的流动性降低,甚至呈半固体状态,宏观剪切应力增加。外加磁场越强,这种聚集程度越大,也就表明磁流变液磁流变效应越强烈。
|
图 2 施加磁场前后磁性颗粒的运动 Fig. 2 Motion of magnetic particle before and after adding magnetic field |
用磁化强度作为磁流变效应强弱的表征量。根据实际磁流变液轴体以及弹性膜的结构、设计,我们假设:磁流变液在弹性薄膜中均匀分布,在磁化过程中不存在某处的特性变化与周围有显著差异;磁流变液在流动过程中与磁流变液腔体因摩擦力会产生些许颗粒残留,但由于数量较少,不对实际试验结果产生影响,故计算中不考虑在内。
则磁性液体整体的磁化强度可通过Langevin函数描述[20]:
| $ M_{{\rm{L}}}=n \int_{0}^{\infty} m(x) L(\alpha) f(x) {\rm d} x\text{,} $ | (1) |
| $ m(x)=\frac{M_{\rm d} {\text{π}}x^{3}}{6}\text{,} $ | (2) |
| $ L(\alpha)=\frac{\operatorname{coth} \alpha-1}{\alpha}\text{,} $ | (3) |
| $ \alpha=\frac{\mu_{0} m H}{k_{\rm B} \theta}\text{,} $ | (4) |
式中,ML为磁性液体的Langevin磁化强度;x为纳米磁性颗粒的直径;n为磁性液体内的颗粒数目;m(x)与m均代表磁性颗粒的磁距;Md为磁性颗粒的磁化强度;f(x)为磁性液体中磁性颗粒的粒径分布函数,一般为对数正态分布的Langevin函数;α表示Langevin参数;μ0为真空磁导率;H为外加磁场强度;kB为玻尔兹曼常数;θ为德拜温度。由式(1)~(4)可知,磁化强度与磁场强度正相关,说明磁性液体的磁流变效应强弱主要受到外加磁场强度影响。磁场强度越大,其内部磁性颗粒聚集越明显,磁化程度越强。
2.2 磁场对磁流变液物理特性的影响要研究磁场对磁流变液流变特性以及喷头流量的影响,首先需求得弹性腔以及磁流变液腔内磁流变液体积变化的表达式:
| $ \Delta {{V}}=V_{0}-V_{1}\text{,} $ | (5) |
式中,V0为初始加注的磁流变液体积,在添加时可确定;V1为施加磁场时磁流变液发生状态改变后磁流变液总体积。
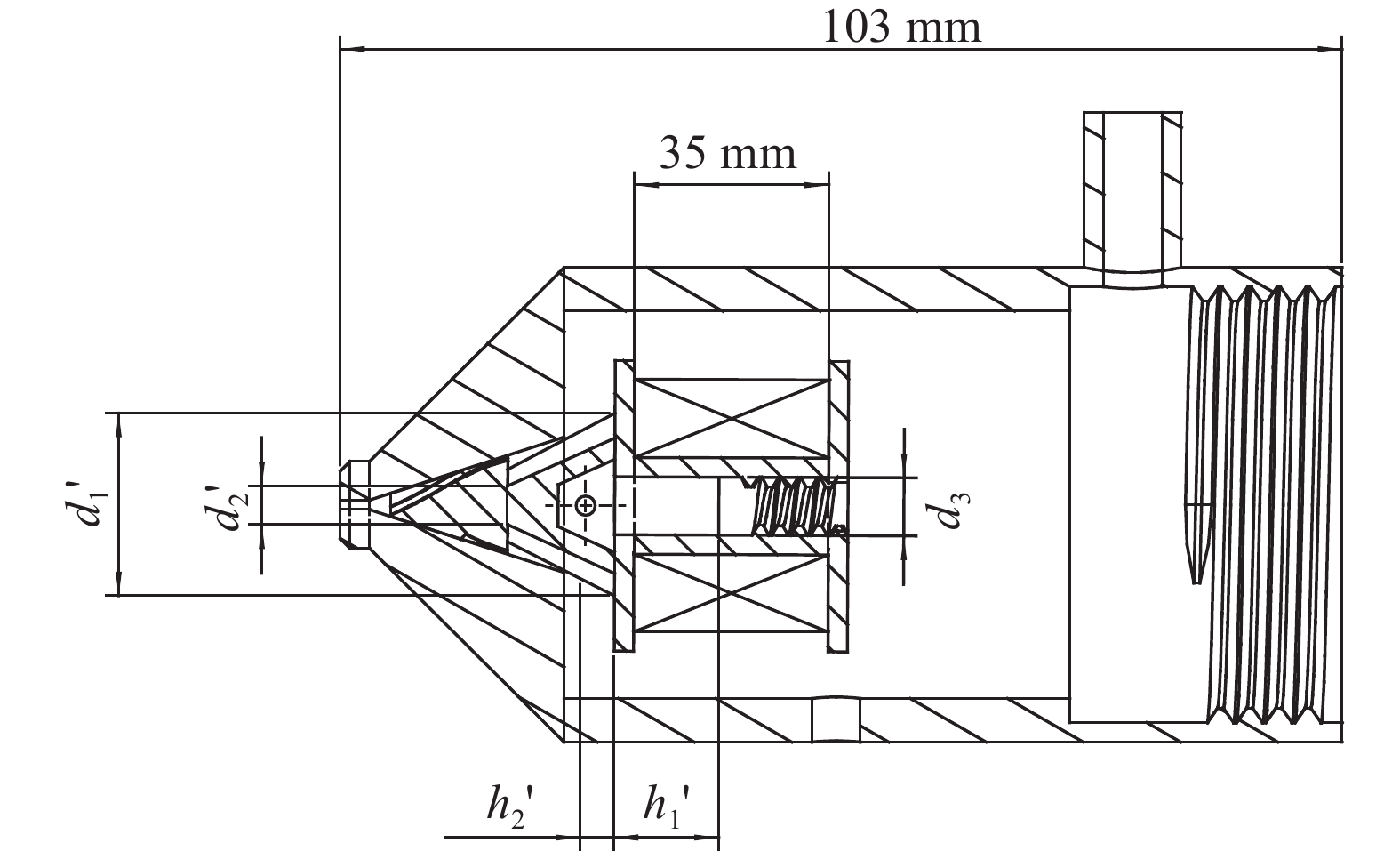
为方便计算,图3中只标注了部分流量计算所涉及的尺寸。当电源接通时,磁流变液被线圈所产生的磁场所吸引,向线圈所在位置聚拢且形态发生变化,认为弹性腔内磁流变液在任何阶段均相对中心轴体均匀分布,则:
|
图 3 喷头计算尺寸示意图 Fig. 3 Diagram of nozzle for size calculation |
| $ \begin{split} V_{1}=&\int_{0}^{h_1^\prime} \pi d_{3}^{2} {\rm{d}} h+\frac{1}{3} \pi \left[ {{{({d_1^\prime} - 2)}^2} + ({d_1^\prime} - 2){d_2}^\prime + {d_2}^\prime } \right]{h_2}^\prime + \\ &\frac{1}{3} \pi\left( {d_1^{\prime 2 } + {d_1}^\prime {d_2}^\prime + d_2^{\prime 2 }} \right){h_2}^\prime\text{,} \end{split} $ | (6) |
式中,h1′为施加磁场后注液通道内磁流变液实际高度;h2′为施加磁场后弹性腔内磁流变液实际高度;d1′为施加磁场后弹性腔磁流变液上表面半径;d2′为施加磁场后弹性腔内磁流变液的底面半径;d3为注液通道半径。
式(6)中,h1′、h2′、d1′、d2′数值与磁流变效应强弱成反比,即磁流变变液体积变化与磁流变效应强弱正相关,同时磁流变液的体积变化直接对雾化腔入口处横截面积产生影响,而液体在通道内的流速与流量均受到通道横截面积变化的影响。磁流变液状态改变前后喷头流量变化(ΔQ)为:
| $ \Delta Q={\rm{\rho}}\left|v_{0} {\rm{cos}} \gamma A_{0}-v_{1} {\rm{cos}} \gamma A_{1}\right|\text{,} $ | (7) |
式中,ρ为液体密度,γ为雾化腔斜面角度;v0为初始液体进入雾化腔的垂直速度;A0为此时入口横截面积;v1为施加磁场后液体进入雾化腔的速度;A1为此时入口横截面积。液体在雾化腔入口处的流速(v)可由下式表述:
| $ v=\frac{R^{\frac{2}{3}} \times J^{\frac{1}{2}}}{\lambda}\text{,} $ | (8) |
| $ R={A}/{x}\text{,} $ | (9) |
式中,J为水力坡度,这里不考虑其影响,则数值为1;R为水力半径;λ为喷头内壁粗糙系数;x为液体接触的内壁横截面周长。
由式(7)、(8)和(9)可得:
| $ \Delta {{Q}}={\rm{\rho}}\left|\lambda \times \frac{A_{0}^{\frac{5}{3}}-A_{1}^{\frac{5}{3}}}{x^{\frac{2}{3}}}\right|{\text{。}} $ | (10) |
对于同一喷头,粗糙系数λ与内壁横截面周长(x)均为恒定值,故可判断其流量主要与雾化腔入口处的有效截面积有关。当雾化腔入口横截面积增大时,液体流速和流量会同时随之增大。磁流变前后磁流变液体积差越大,雾化腔入口横截面积变化越大,喷头流量变化越大。由式(1)(5)(6)可知,磁流变液体积变化程度由线圈磁场强度决定。而物理学常用磁感应强度代替磁场强度进行磁场计算(两者呈线性关系),其大小主要由线圈的参数决定,所以励磁线圈的设计很重要。考虑到机械加工水平、实际尺寸等限制,本文磁流变液装置的励磁线圈定为多层圆环电压线圈。
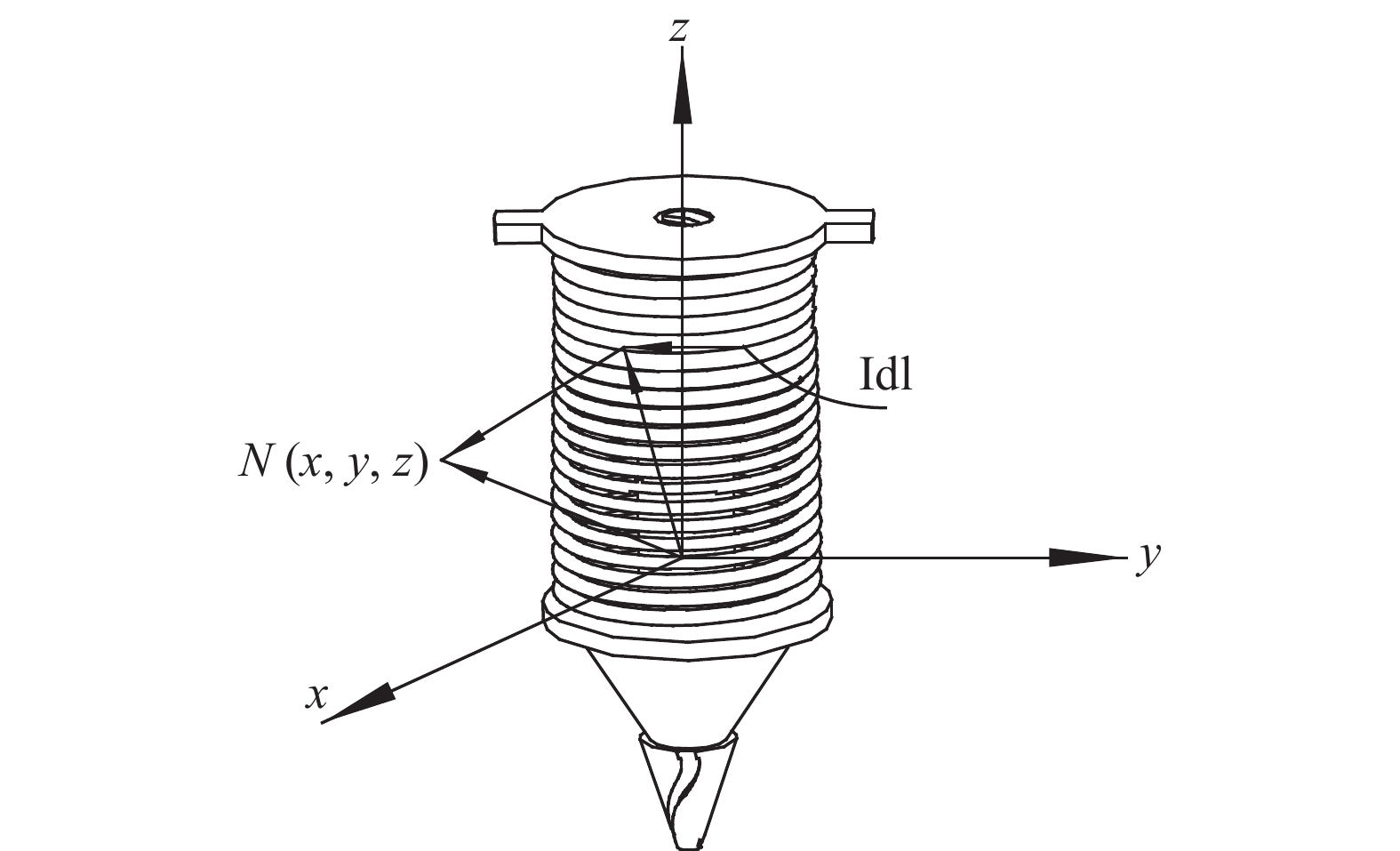
2.3 线圈磁感应强度的模拟设计圆环励磁线圈半径保持恒定,改变线圈绕制匝数、导线直径、长度以及施加电压的大小,对磁感应强度以及磁流变液形态可能产生不同程度的影响[21]。设所绕环形线圈截面最内层与最外层半径分别为为r1、r2,线圈通电电流为I。如图4所示,设某一电流元为Idl(微量),其路径经过某一水平横截面为x-y平面,坐标原点与横截面圆心重合,线圈中心轴与z轴重合。
|
图 4 圆环线圈磁场分析图 Fig. 4 Analysis of toroidal coil magnetic field |
相关研究通过毕奥−萨伐尔定律对圆环线圈周围磁场分布进行了推导[22],得出N点在x、y、z轴3个方向的磁感应强度分量Bx、By、Bz:
| $\begin{split} {B_x} = & \frac{{{u_0}US{r}z}}{{4\text{π} \rho L}} \\ & \int_0^{2\text{π} } {\frac{{{\rm{cos}} \phi {\rm{d}}\phi }}{{{{\left[ {{x^2} + {y^2} + {z^2} + r^2 - 2{r}(x \cos \phi + y \sin \phi )} \right]}^{\frac{3}{2}}}}}} {\text{,}} \end{split} $ | (11) |
| $\begin{split} {B_y} = & \frac{{{u_0}US{r}z}}{{4\text{π} \rho L}} \\ & \int_0^{2\text{π} } {\frac{{\sin \phi {\rm{d}}\phi }}{{{{\left[ {{x^2} + {y^2} + {z^2} + r^2 - 2{r}(x \cos \phi + y \sin \phi )} \right]}^{\frac{3}{2}}}}}} \end{split}{\text{,}} $ | (12) |
| $\begin{split} B_{z}= & \frac{u_{0} U S r}{4 \text{π} \rho L} \\ & \int_{0}^{2 \text{π}} \frac{\left(r-x \cos \phi-y \sin \phi\right) {\rm{d}} \phi}{\left[x^{2}+y^{2}+z^{2}+r^{2}-2 r(x \cos \phi+y \sin \phi)\right]^{\frac{3}{2}}}{\text{,}} \end{split} $ | (13) |
| $ r = \frac{{{r_2} - {r_1}}}{{\ln {r_2} - \ln {r_1}}}{\text{,}} $ | (14) |
式中,x、y、z分别为N点在3个方向的坐标,U为输入电压。r为等效半径,用于将多层线圈转化为单层圆环线圈进行磁感应强度计算。ρ为导体电阻率,L为导线长度,S为导线横截面积,
参考文献[23]的方法,根据公式通过Matlab软件编写程序对磁流变液喷头工作的磁场分布进行仿真分析。设定圆环线圈中心为坐标原点,真空磁导率为4
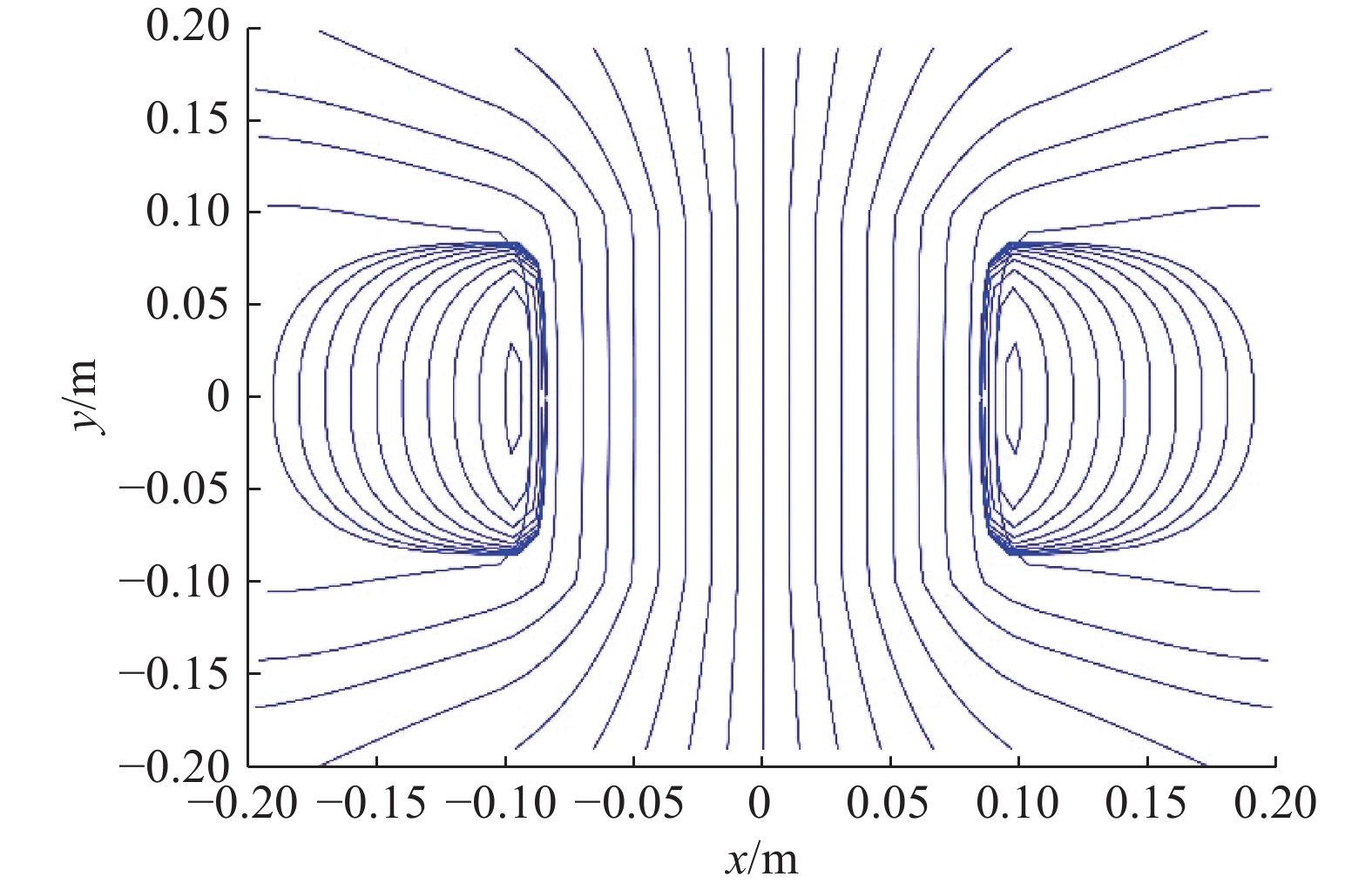
|
图 5 x=0平面磁场分布矢量图 Fig. 5 Vector graph of magnetic field distribution at x=0 plane |

|
图 6 x=0平面任一点的磁场分布 Fig. 6 Magnetic field distribution of faculative point at x=0 plane |
由图6可以看出,对于x=0平面内任一点,其分量在较小的可视区域内由坐标原点沿y轴与z轴均逐渐增大。而Bz分量由原点沿y轴逐渐增大,沿z轴逐渐减小。在线圈中心轴线上,其By分量为0,只有Bz分量。图5与图6的分布符合理论规律,同时可以判定磁流变液腔的布局处于磁场分布较密集的区域。
2.4 线圈参数的确定依据计算与仿真结果分析,绕制线圈时应在选取较粗导线的同时确保尽可能多的线圈匝数。一般线圈圆心处磁感应强度大于30 mT时才会对磁流变液宏观特征产生显著影响[24]。而铜线线圈漆包线直径一般为0.06~2.24 mm[25]。设定线圈最外层半径为15 mm,在线圈电压12 V时,在圆心处磁感应强度为30 mT的线圈漆包线单位长度电阻计算为0.26 Ω·m−1,查表可知此时相对应的线径为0.28 mm。即当线径大于0.28 mm时所产生的磁感应强度才可能符合要求。同时为防止电流过大以及漆包线过细而造成磁路在高温下受到的损害,小型励磁线圈线径应保持为0.2~1 mm范围内。因此分别选取0.3、0.5、0.8和1.0 mm线径的漆包线进行绕制,并用高斯计对其接通电源后产生的磁场感应强度进行测定。几组测试中高斯计均放置在线圈一端的中心轴线处进行测量,测得几种参数的线圈在12和24 V电压下磁感应强度如表1所示。
|
|
表 1 线圈实测磁感应强度 Table 1 Measurement of coil magnetic field |
实际测试中,不同规格线圈所产生的磁感应强度受绕制精度、层数等因素的影响,与理论值有一定偏差。为精简线圈尺寸在所产生磁感应强度相当的情况下应选择线圈高度较小的漆包线规格。最终选择0.5 mm线径规格漆包线,线圈高度定为35 mm。
3 材料与方法 3.1 试验材料与设备测试在华南农业大学荷园喷施雾化实验室进行,室内场地宽阔,不受自然风、光照等因素影响,试验数据稳定可靠。喷雾平台包括兆信KXN-6010D以及龙威LW-6020KD直流电源、水箱、支架、普兰迪PLD-1206隔膜泵、方威DN-15减压阀、红旗Y-100压力表等。测试喷头准备几种装有不同剂量磁流变液的磁流变液喷头,以流量范围相近的Lechler F110-02VS型号液力式喷头(Lechler公司生产,其喷雾角为110°,雾化形状为平面扇形)作为对照组,试验因素设定见表2。
|
|
表 2 试验因素设定 Table 2 Setting of testing factors |
按照图7所示搭建试验平台,依次连接好水泵电源、线圈电源、水箱、水泵、水管、调压阀和压力表。

|
图 7 试验平台 Fig. 7 Testing platform 1:减压阀;2:线圈电源;3:水泵电源;4:压力表;5:磁流变液喷头;6:喷雾支架;7:隔膜泵;8:水桶 1:Reducing valve;2:Coil battery;3:Power of water pump;4:Piezometer;5:Magnetorheological nozzle;6:Spraying frame;7:Water pump;8:Water bucket |
首先测试磁流变液注入量对喷施流量的影响。调节水泵泵压使其恒定在0.3 MPa,安装Lechler110-02VS喷头进行流量测试并记录数据,然后将准备好的磁流变液注入量分别为0、0.5、1.0、1.5、2.0、2.5 mL的喷头依次与水管连接安装,在线圈电压初始状态为0时打开电源开关,测试此时流量;然后分别将线圈电压升至12、24 V继续测试流量。每组试验重复3次。
为进一步测试喷头流量受线圈电压改变的影响。在测试1.5 mL磁流变液注入量的喷头流量时增加6、18和28 V的电压梯度,依次测试流量。每组测试重复3次。
4 结果与分析 4.1 磁流变液注入量对喷施流量的影响当隔膜泵泵压为0.3 MPa时,磁流变液喷头随不同磁流变液注入量的流量变化如图8所示。从图8可以发现,在无磁流变液注入的情况下,磁流变液喷头的流量为0.91 L/min,大于Lechler F110-02VS喷头的流量0.8 L/min;当施加磁场(线圈通电)时,3种线圈电压(0、12、24 V)下磁流变液喷头的流量随着不同的磁流变液注入量变化趋势一致,均随着磁流变液注入量的增加而减小,在2.5 mL磁流变液注入量时分别降至0.65、0.69和0.78 L/min。此时3种情况下磁流变液喷头的流量均小于Lechler F110-02VS的流量。当电压为0时喷头流量下降趋势相比通12 V电压时稍快,两者都明显比通24 V电压时下降更剧烈。说明线圈电压越大,会对喷头的流量下降起到阻抗作用,使其下降趋势放缓。

|
图 8 喷头流量随磁流变液注入量变化曲线 Fig. 8 Variation of nozzle flow rate with change of magnetorheological fluid injection volume |
当磁流变液注入量为1.5 mL时,喷头流量随电压的变化如图9所示。由图9可知,喷头流量的增长曲线可分为3个阶段:当线圈电压小于6 V时,电压对喷头流量的影响很不明显,一直稳定在0.72 L/min,说明此时电压过小,所产生的磁感应强度难以对磁流变液产生实质影响;当电压为12~18 V时,喷头的流量呈现持续快速上升趋势,由0.72 L/min上升到了0.85 L/min,增加了18%。此时线圈开始对磁流变液产生明显的聚集作用,对流量的影响最显著;当电压超过24 V时,喷头流量逐渐趋于稳定,在0.9 L/min上下浮动。这是由于当电压超过一定限度时,其磁流变效应对喷头内部结构造成的改变已经接近饱和,即使继续增加电压理论上也不会再对流量产生影响。

|
图 9 喷头流量随线圈电压变化曲线 Fig. 9 Variation of nozzle flow rate with change of coil voltage |
本文利用磁流变液的流变特性设计了农用变量喷头,对其进行理论分析与参数优化,并对磁场的磁感应强度进行了MATLAB仿真;搭建了喷雾试验平台,对磁流变液喷头流量受磁流变液注入量和线圈电压的影响进行测试,得出以下结论:
1) 在磁流变液喷头未注入磁流变液时,同等条件下其流量稍大于Lechler110-02VS扇形喷嘴的流量。随着磁流变液注入量的增加,其流量呈减小趋势并逐渐低于Lechler110-02VS扇形喷嘴流量。当线圈通电时,线圈电压越大,喷头流量随磁流变液注入量而变化的趋势越缓慢。
2) 当磁流变液注入量保持恒定时,磁流变液喷头流量随着线圈电压的增大而增大,当电压升高到某一数值时,线圈所产生的磁场对磁流变液的影响达到最大,之后喷头流量趋于稳定。
3) 本文所设计磁流变液喷头可以初步达到调节流量的目的,且响应时间较短。但其可靠性还有待加强,同时流量调节范围相对其他流量调节方式较小。后续应对线圈以及喷体内部结构进行优化,如在铜线内侧添加铁芯增强磁场等。同时喷头质量偏重,应进一步向轻量化改进。后续研究将装载于无人机进行试验。
国内外关于将磁流变液的特性应用于喷头流量调控的研究较少,因此本文所述是一种全新的流量调节方法。本研究尚处于初步阶段,但其对农用喷头乃至工业喷头的设计与改进均具有重要参考意义。
| [1] |
兰玉彬, 彭瑾, 金济. 农药喷雾粒径的研究现状与发展[J]. 华南农业大学学报, 2016, 37(6): 1-9. (  0) 0) |
| [2] |
FRITZ B K, HOFFMANN W C, CZACZYK Z, et al. Measurement and classification methods using the ASAE S572: 1 reference nozzles[J]. J Plant Prot Res, 2012, 52(4): 447-457. DOI:10.2478/v10045-012-0072-x (  0) 0) |
| [3] |
张东彦, 兰玉彬, 陈立平, 等. 中国农业航空施药技术研究进展与展望[J]. 农业机械学报, 2014, 45(10): 53-59. DOI:10.6041/j.issn.1000-1298.2014.10.009 (  0) 0) |
| [4] |
HUANG Y, THOMSON S J, HOFFMANN W C, et al. Development and prospect of unmanned aerial vehicle technologies for agricultural production management[J]. Int J Agric Biol Eng, 2013, 6(3): 1-10. (  0) 0) |
| [5] |
LEBEAU F, ELBAHIR L, DESTAIN M F, et al. Improvement of spray deposit homogeneity using a PWM spray controller to compensate horizontal boom speed variations[J]. Comput Electron Agric, 2004, 43(2): 149-161. DOI:10.1016/j.compag.2004.01.001 (  0) 0) |
| [6] |
BRUNO S. FAIÇAL, PESSIN G, FILHO G P R, et al. Fine-tuning of UAV control rules for spraying pesticides on crop fields[C]//IEEE international conference on tools with artificial intelligence. Cyprus: IEEE, 2014: 527-533.
(  0) 0) |
| [7] |
王玲, 兰玉彬, 陈度, 等. 微型无人机低空变量喷药系统设计与雾滴沉积规律研究[J]. 农业机械学报, 2016, 47(1): 15-22. (  0) 0) |
| [8] |
王浩, 陈树人. 基于PWM的变量喷施控制系统设计及实验研究[J]. 农机化研究, 2012, 34(12): 159-161. DOI:10.3969/j.issn.1003-188X.2012.12.039 (  0) 0) |
| [9] |
杨健健, 晏华, 代军, 等. 磁流变液材料的性能与应用综述[J]. 化工进展, 2017, 36(1): 247-260. (  0) 0) |
| [10] |
BERKOVSKY B M, MEDVEDEV V F, KRAKOV M S. Magnetic fluids: Engineering applications[M]. Oxford: Oxford University Press, 1993.
(  0) 0) |
| [11] |
HUANG Y, HOFFMANN W, LAN Y, et al. Development of a low-volume sprayer for an unmanned autonomous helicopter[J]. J Agric Sci, 2014, 7(1): 148-153. (  0) 0) |
| [12] |
周晴晴, 薛新宇, 钱生越, 等. 航空喷嘴的使用现状及研究方向[J]. 中国农机化学报, 2016, 37(10): 234-237. (  0) 0) |
| [13] |
文晟, 兰玉彬, 张建桃, 等. 农用无人机超低容量旋流喷嘴的雾化特性分析与试验[J]. 农业工程学报, 2016, 32(20): 85-93. DOI:10.11975/j.issn.1002-6819.2016.20.011 (  0) 0) |
| [14] |
中华人民共和国国家质量监督检验检疫总局. 农业灌溉设备非旋转式喷头技术要求和试验方法: GB/T 18687—2012[S]. 北京: 中国标准出版社, 2013.
(  0) 0) |
| [15] |
金春玉. 空心圆锥雾化喷嘴喷雾实验与数值研究[D]. 上海: 上海交通大学, 2007.
(  0) 0) |
| [16] |
王晓琦. 压力旋流喷嘴设计和实验研究[D]. 北京: 中国石油大学, 2007.
(  0) 0) |
| [17] |
张海平. 轴流风速下压力旋流喷嘴外流场特性研究[D]. 北京: 中国石油大学, 2009.
(  0) 0) |
| [18] |
杨春成. 磁性液体的磁性及磁粘性质研究[D]. 济南: 山东大学, 2016.
(  0) 0) |
| [19] |
TRIPATHI D, BEG O A. A study of unsteady physiological magneto-fluid flow and heat transfer through a finite length channel by peristaltic pumping[J]. P I Mech Eng H, 2012, 226(8): 631-644. DOI:10.1177/0954411912449946 (  0) 0) |
| [20] |
袁姝. 电磁场参数对磁流变液特性的影响及优化研究[D]. 上海: 上海工程技术大学, 2016.
(  0) 0) |
| [21] |
杨小龙, 李德才, 杨文明, 等. 磁流体密封的磁路设计及磁场有限元分析[J]. 真空科学与技术学报, 2012, 32(10): 919-922. DOI:10.3969/j.issn.1672-7126.2012.10.12 (  0) 0) |
| [22] |
周敏, 田大庆, 李小润, 等. 多层圆线圈在电磁计算中全空间磁感应强度B的分布[J]. 制造业自动化, 2016, 38(3): 18-19. (  0) 0) |
| [23] |
胡国良, 李海燕, 张海云. 圆环流磁流变阀压降性能分析与试验[J]. 农业机械学报, 2016, 47(3): 381-388. (  0) 0) |
| [24] |
卜胜利, 吴龙龙. 磁流体的Shliomis体积特性研究[J]. 上海理工大学学报, 2015, 37(5): 419-424. (  0) 0) |
| [25] |
沈阳变压器研究所. 变压器线圈制造[M]. 北京: 机械工业出版社, 1983.
(  0) 0) |
 2019, Vol. 40
2019, Vol. 40


