2. 东南大学 仪器科学与工程学院,江苏 南京 210096
2. College of Instrument Science and Engineering, Southeast University, Nanjing 210096, China
科学技术的进步正推动现代农业生产向自动化、规模化、精确化方向快速发展,具备自主导航功能的农业机械越来越多地应用到农业生产中[1]。自主导航拖拉机作为牵引机械能够高效完成田间播种、施肥和耕地[2-7],自主导航联合收割机能够在无人干预的情况下收获小麦、水稻和玉米[8-13]。当农机工作环境中出现少量障碍物时,障碍物可能会阻碍农机正常工作,因此规划一条建立在农机工作平台上的避障路径、帮助农机在存在障碍物的环境中正常完成作业任务必不可少。
现阶段国内外关于农机平台避障路径规划的研究较少,国内研究更多建立在无障碍物环境中,刘刚等[14]提出一种基于GNSS的农田平整自动导航路径规划方法,实现拖拉机的高效平地作业;孟志军等[15]提出一种面向农田作业机械的地块全区域覆盖路径优化方法,以生成转弯数最少、作业消耗最小、总作业路径最短或有效作业路径比最大的最优作业路径。国外学者针对有障碍物环境展开了相应的研究,Taïx等[16]针对农田中小型静态障碍物提出一种折线避障方法,虽能实现避障功能,但避障代价过大,且未充分考虑农机的运动特性;圆弧避障方法是现阶段应用较为广泛的一种避障路径规划方法,但避障策略较为简单,当障碍物间距离较近时会出现算法失效的情况。现阶段成熟的路径规划算法如A-star算法[17-18]、SA算法[19]和人工势场法[20-21]等大多运用在农业机器人和AGV小车[22-26]等小型精准控制平台上,这些算法倾向于将控制物体等效于一个运动点,但运用在农机平台(如东方红SG250拖拉机)上时,将农机等效为单个运动点会丢失大量的农机自身运动模型信息。算法提供的控制策略也未充分考虑应用在农机平台的可行性,使得现阶段传统路径规划算法或其改进版无法适用于农机工作平台。
为了自主导航农业机械能够顺利避障,建立在农机自身运动模型以及农机工作环境基础上的避障路径规划必不可少。规划的路径指导自主导航农业机械在工作过程中以尽量小的避障代价实现障碍物的避障,并在避障完成后合理地回归原始工作路径,因此,自主导航农业机械避障路径规划的研究具有很强的实际意义。
1 避障路径规划算法 1.1 单障碍物避障路径规划算法 1.1.1 判断障碍物的威胁性确定障碍物位置后,需判断障碍物是否会对拖拉机正常工作产生影响,具体工作流程如下:
1) 以一矩形示意表达拖拉机模型,以矩形中心O为原点建立平面坐标系,x轴正方向为水平向右,y轴正方向与拖拉机航向重合。
2) 以障碍物几何中心Z(XZ,YZ)为圆点,Z到障碍物边界的最长距离RZ为半径作圆,构建防碰撞区域。
3) 计算Z到y轴距离d,设d和RZ的差值为c,比较c与半车宽L/2的大小。若c>L/2,为无威胁障碍物;反之为有威胁障碍物。
4) 当障碍物为无威胁障碍物时,拖拉机可沿原有导航路线继续自主导航;当障碍物为有威胁障碍物时,拖拉机需根据障碍物位置以及自身运动模型更新避障路径。如图1所示,障碍物Z为有威胁障碍物。

|
图 1 避障安全距离的计算 Fig. 1 Calculation of safety distance for obstacle avoidance |
若障碍物为有威胁障碍物,需计算避障安全距离(D),如果在自主导航过程中拖拉机与障碍物的距离小于D,即使以最大偏转角避障,拖拉机仍然会与障碍物碰撞。图1中,当拖拉机采用最大偏转角避障时,拖拉机转弯半径为最小转弯半径。具体的计算方法如下:
1) 设拖拉机最小转弯半径为rL,则拖拉机转向中心X1位置为(−rL,0),连接X1与矩形右上角点F(XF,YF),以X1为圆心,X1到F距离为半径作圆,则圆X1为拖拉机右侧边界角点行驶轨迹图。
2) 拖拉机向前行驶时,圆X1在坐标轴上会随之沿y轴方向平移,若平移后的圆X1′与防碰撞区域圆Z相切,设此时的圆心坐标X1′为(−rL,y),则变量y满足方程:
| $\sqrt {{{\left( { - {r_L} - {X_Z}} \right)}^2} + {{\left( {y - {Y_Z}} \right)}^2}} - {R_Z} = \sqrt {{{\left( {{X_F} + {r_L}} \right)}^2} + {{\left( {{Y_F} - {0}} \right)}^2}} $ |
解得y值,计算YZ与y的差值D,D为避障安全距离。
3) 设拖拉机当前所在位置yO与YZ的差值为dOZ,若dOZ小于D,则拖拉机无法成功避障,应立即停止工作,防止与障碍物产生碰撞。
4) 由步骤2)确定拖拉机可向前行驶的安全距离区间为[0,YZ−D],为使拖拉机尽可能地跟踪初始路径,尽量贴近障碍物后再执行避障动作,可将该区间分成若干段[0,d1]、(d1,d2]、(d2,d3]…(dn−1,dn],拖拉机在行进一段安全距离dn(n=1, 2, 3, 4…)后再进行避障路径规划并计算避障总代价,筛选出一条代价最小的避障路径作为最终的避障路径,n的大小根据实际避障时具体D值决定。
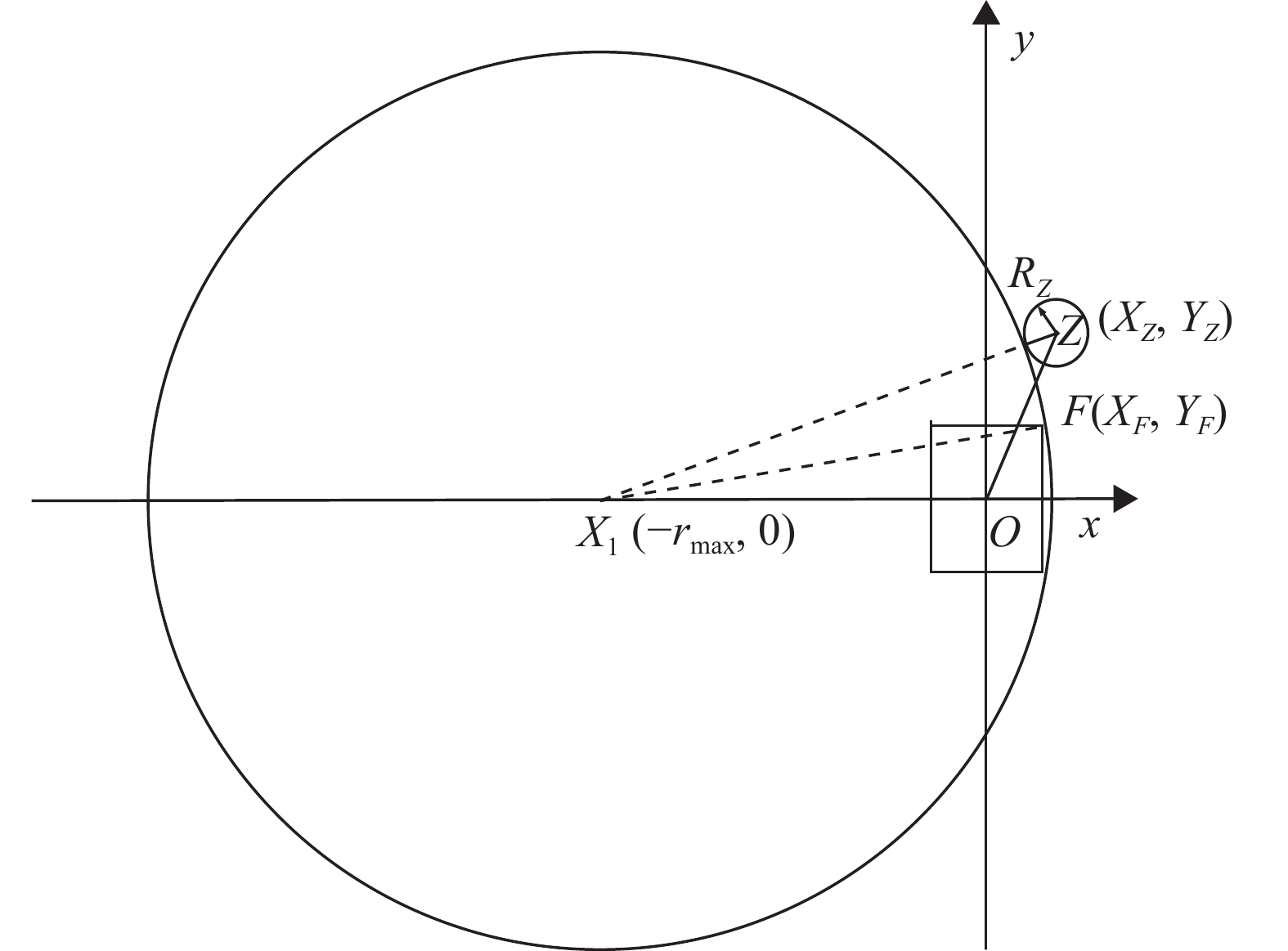
1.1.3 避障最大转弯半径的确定1) 如图2所示,当拖拉机向前行驶由1.1.2确定的一段避障安全距离后,便可以计算拖拉机的避障代价,但在此之前需根据障碍物的位置先确定拖拉机避障最大转弯半径,设拖拉机能够避障的最大转弯半径为rmax,则可确定拖拉机的初始转向中心X1的位置为(−rmax,0)。
|
图 2 确定避障最大转弯半径 Fig. 2 Determination of the maximum turning radius of obstacle avoidance |
2) 根据拖拉机避障过程中临界碰撞条件“拖拉机右边界运动轨迹与圆Z相切”,列出方程:
| $\sqrt {{{\left( {{X_Z} + {r_{\max}}} \right)}^{^2}} + {{\left( {{Y_Z} - 0} \right)}^{2}}} - {R_Z} = \sqrt {{{\left( {{X_F} + {r_{\max}}} \right)}^{2}} + {{\left( {{Y_F} - 0} \right)}^{2}}} $ |
3) 解方程,得避障最大转弯半径rmax。
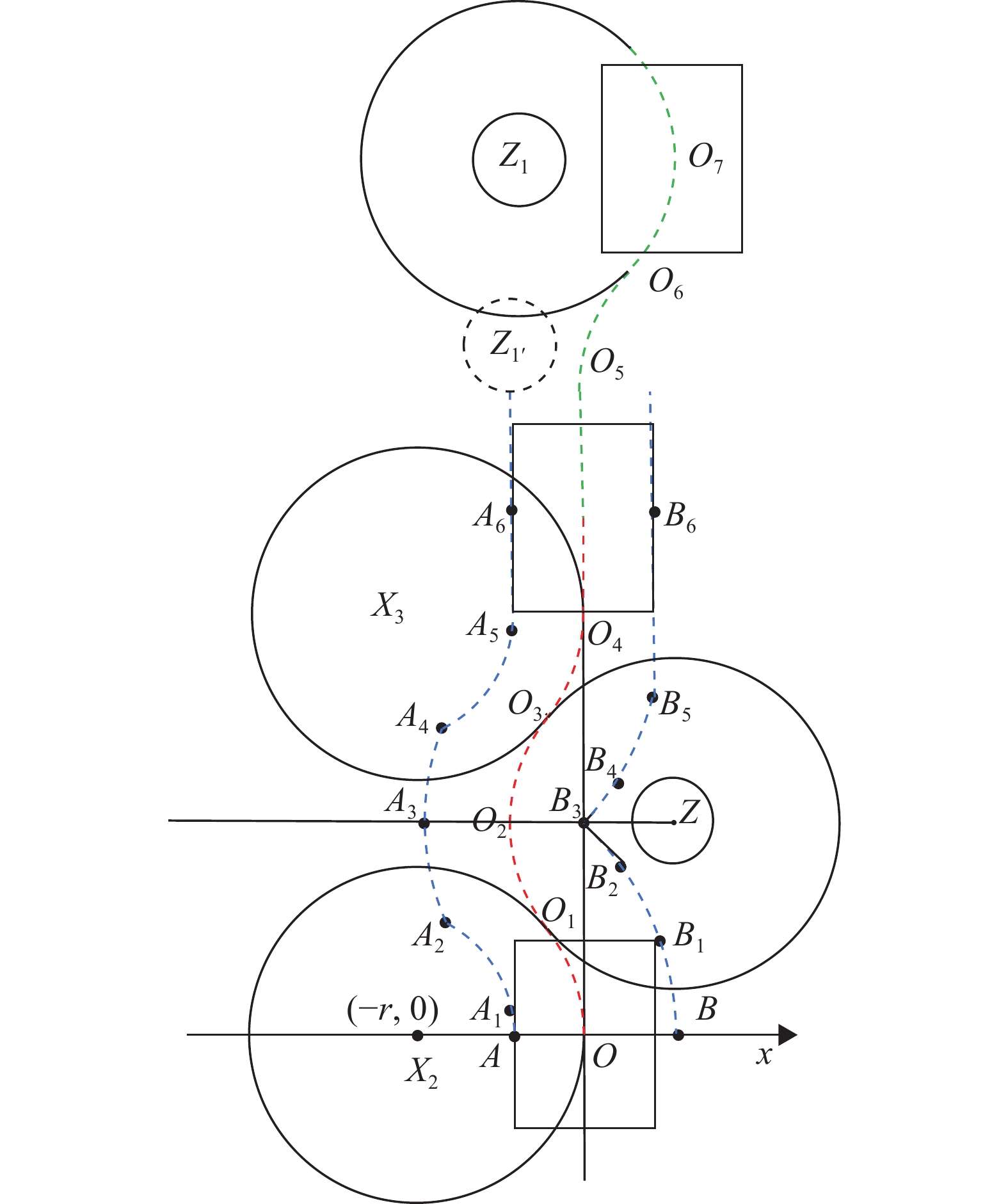
1.1.4 4段路径规划1) 设车辆实际转向半径为r(r≤rmax),则实际转向中心X2为(−r,0)。以X2为圆心,r为半径作圆X2,如图3所示:
|
图 3 单/双障碍物避障算法 Fig. 3 Single obstacle/double obstacles avoidance algorithm |
2) 连接圆心X2与Z点,与圆X2相交于O1点,则
3) 以Z为圆心,以ZO1距离为半径作圆,与直线y=YZ交于O2点,则
4) 作O1点关于直线y=YZ的对称点O3,则
5) 作X2关于直线y=YZ的对称点X3,以X3为圆心,X3到O3点的距离为半径作圆X3,与y轴相切于O4点,则
考虑到自主导航拖拉机在偏转角控制上存在一定的滞后与误差,因此在避障路径的规划过程中应尽量减少偏转角变化的次数。4段圆弧避障路径仅在O1与O3点要求拖拉机偏转角发生改变,以帮助拖拉机实现最基本的避障与回归原始路径功能。若是3段圆弧路径则只能实现避障功能,拖拉机在完成避障后无法回归原始航线。若是5段圆弧路径,则每段圆弧长度被压缩得相对较短,且会发生3次偏转角变化,实际操作时会放大拖拉机偏转角控制存在误差与滞后的问题,使得拖拉机难以跟踪规划路径。因此,对于拖拉机控制平台4段圆弧路径规划更稳定,实际操作时更易实现。
1.1.5 避障代价的计算 1) 以4段避障路径总长度S为避障代价,S由
2) 设O1X2与x轴的夹角为θ,则θ的大小为:
| $\theta = \arctan \frac{{{Y_Z}}}{{{X_Z} + r}}{\text{。}}$ |
| $ \begin{array}{c} {S_1} = \dfrac{{{\text{π}}r}}{{180}} \arctan \dfrac{{{Y_Z}}}{{{X_Z} + r}}{\text{,}}\\ {S_2} = \dfrac{{{\text{π}}\left( {\sqrt {{{\left( {{X_Z} + r} \right)}^2} + {Y_Z}^2} - r} \right)}}{{180}} \arctan \dfrac{{{Y_Z}}}{{{X_Z} + r}}{\text{,}}\\ {S_3} = \dfrac{{{\text{π}}\left( {\sqrt {{{\left( {{X_Z} + r} \right)}^2} + {Y_Z}^2} - r} \right)}}{{180}} \arctan \dfrac{{{Y_Z}}}{{{X_Z} + r}}{\text{,}}\\ {S_4} = \dfrac{{{\text{π}}r}}{{180}} \arctan \dfrac{{{Y_Z}}}{{{X_Z} + r}}{\text{,}} \end{array}$ |
3) 设
则S关于转向半径r的函数为:
| $\begin{align} S = & {S_1} + {S_2} + {S_3} + {S_4}= \\ & \frac{{{\text{π}} \left( {\sqrt {{{\left( {{X_Z} + r} \right)}^{2}} + {Y_Z}^{2}} } \right)}}{{90}} \arctan \frac{{{Y_Z}}}{{{X_Z} + r}}{\text{。}} \end{align} $ |
4) 在r∈[rL,rmax]区间内,计算可得S最小时的r取值。其中rL为车辆最小转弯半径,可从车辆说明书中获得,rmax为1.1.3确定的车辆避障最大转弯半径。
1.1.6 避障总行驶路径的计算自主导航拖拉机执行避障动作时,需确定避障起始点,由1.1.2可确定允许拖拉机向前行驶的距离为d1、d2、d3、d4…dn,以1.1.4、1.1.5方法计算相对应的n个避障代价S1、S2、S3…Sn,最终拖拉机完成避障动作所需的总路径长度为Cn = Sn+dn,当Cn为最小时,设此时规划的避障路径为最优避障路径,此时确定的拖拉机转弯半径r为最优转弯半径。
1.2 双/多障碍物避障路径规划算法单障碍物避障算法适用于路径上出现单一障碍物的情况,当拖拉机自主导航行驶路径上出现2个障碍物时,可使用双障碍物避障算法予以解决。
1.2.1 障碍物Z避障路径规划首先根据障碍物Z的位置,由单障碍物避障算法进行初始避障路径规划。
1.2.2 构建安全行驶区域如图3所示,完成路径规划后,构建障碍物Z的安全行驶区域,该部分覆盖拖拉机避障经过的所有区域,在图中由A、A1…A6,B、B1…B6以及拖拉机两侧边界延长线构成。
1.2.3 判断障碍物是否存在威胁首先为障碍物Z1构建防碰撞安全区域,并判断是否会与1.2.2建立的安全行驶区域产生交集。若产生交集,说明Z1存在威胁;若无交集,则Z1无威胁,原有路径无需做出修改,拖拉机可正常行驶通过。
1.2.4 判断障碍物远近属性若障碍物Z1存在威胁,则需对障碍物远近属性进行判断。如图3所示,当拖拉机沿着O1…O4完成障碍物Z的避障后回归原始航线,中心O点随之运动到O4,以O4点为原点重新建立避障坐标系,拖拉机可利用单障碍物避障算法沿着O5、O6、O7 3个点再次实现Z1的避障,此时称Z1为远障碍物。当拖拉机完成Z的避障后回归原始航线,若Z1和拖拉机距离已小于避障安全距离D,拖拉机无法完成Z1的避障,此时称障碍物Z1为近障碍物,如图3所示,Z1′为近障碍物,Z1为远障碍物。
1.2.5 近障碍物避障若障碍物Z1为近障碍物,则要求拖拉机在障碍物Z的避障过程中,利用单障碍物避障算法对Z1进行实时避障路径规划,帮助拖拉机完成Z1的避障。
在Z避障过程中,根据Z1位置,单障碍物避障算法会采取左、右避障2种不同的避障策略:
1) 左避障策略。如图4所示,若拖拉机在障碍物Z的避障过程中行进到O2点时,障碍物Z1处在拖拉机航向右侧,此时应采取左避障策略,沿O2…O5完成避障后,拖拉机距离初始路径较远,此时拖拉机应尽快回归初始路径,为保持拖拉机运动连贯性,以Z1为圆心,Z1O5为半径作圆X4。作圆X5与Y轴、圆X4相切于O6、O7 2个点,圆X5半径与圆X3半径相同,圆X3提供Z1左避障时的第1段避障圆弧

|
图 4 左避障与右避障策略 Fig. 4 Strategies of left and right obstacle avoidance |
2) 右避障策略。如图4所示,若拖拉机在障碍物Z的避障过程中行驶经过O2点而继续行进到O2′点时,Z1处在拖拉机航向左侧,此时应采取右避障策略,完成避障后,与1)存在相同的问题,同样以圆X2半径作圆X6,圆X6与圆X4、Y轴相切于O10、O11 2个点,圆X2提供Z1右避障时的第1段避障圆弧
多障碍物避障算法建立在双障碍物避障算法之上,当拖拉机采用单障碍物避障算法实现第1个障碍物的避障动作后,利用双障碍物避障算法可实现第2个障碍物的避障。若存在第3个障碍物,则可在拖拉机完成第2个障碍物的避障后再次调用双障碍物避障算法。以此类推,实现第n−1个障碍物Zn-1的避障后,可调用双障碍物避障算法实现障碍物Zn的避障。
2 避障路径规划试验及结果分析 2.1 试验设计以具备调速和自主导航功能的东方红SG250拖拉机作为试验平台,为使GPS系统正常工作,选择在光线条件良好的晴天的上午开展试验。GPS采用载波相位实时差分技术,定位精度达cm级,将拖拉机跟踪避障路径时的GPS定位数据作为参考标准,以此验证算法的可行性,试验在南京农业大学工学院车库场地进行,如图5所示。

|
图 5 试验平台和试验场地 Fig. 5 Experiment platform and field |
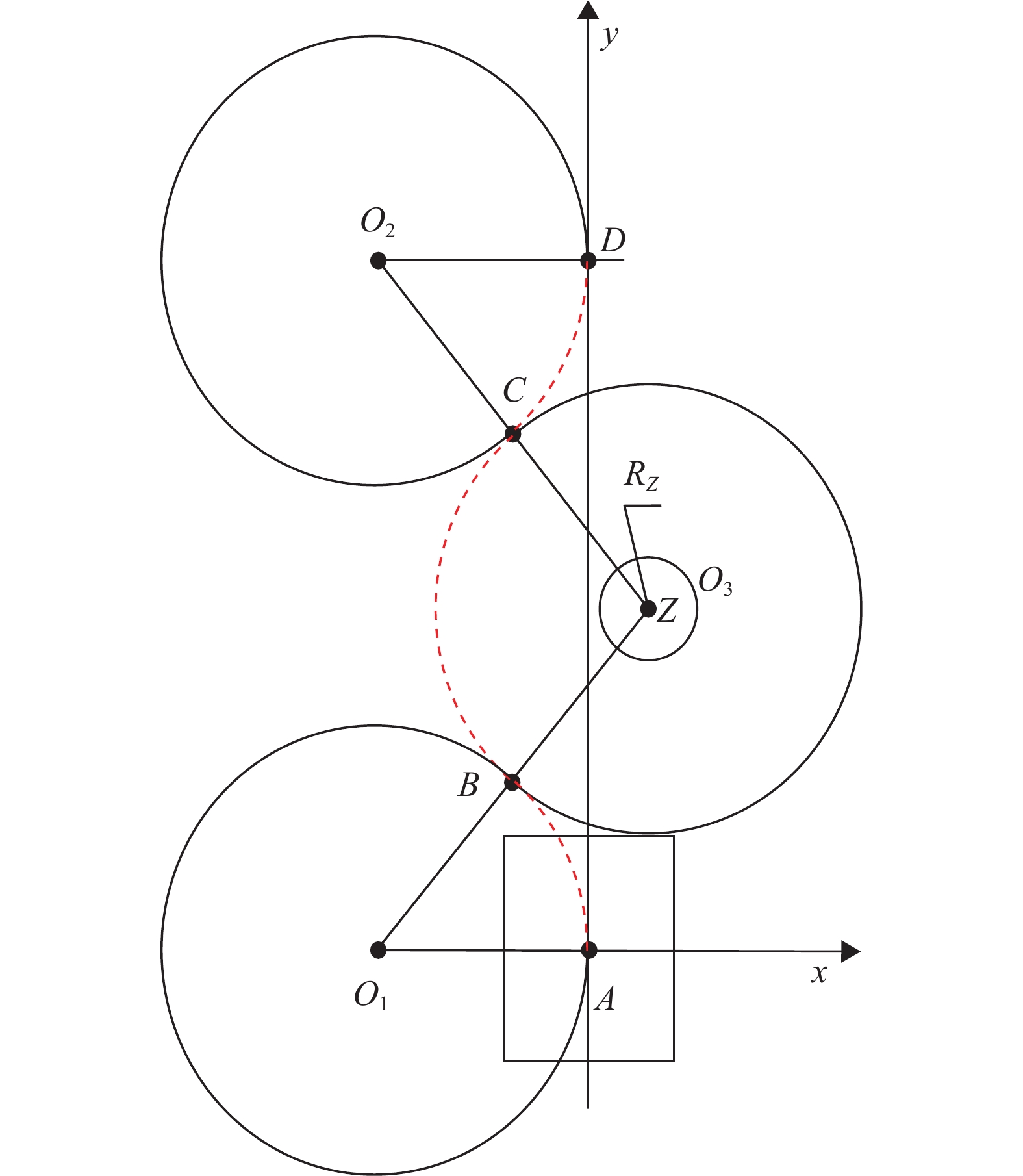
现阶段针对静态障碍物避障路径规划的研究较少,文献[27]提出的避障路径规划算法是现阶段使用较为广泛的方法,与本文所提算法相比,在面对障碍物时均采用4段圆弧避障的形式,具有一定的参考对比价值。下文以L算法指代,利用L算法规划避障路径可通过图6复现。算法由3段圆弧组成,圆弧半径均为拖拉机最小转弯半径,避障路径由
|
图 6 L算法规划避障路径 Fig. 6 L algorithm planning obstacle avoidance path |
试验分为单障碍物避障试验与双障碍物避障试验,障碍物为随机设置,试验前由Bumblbee2双目相机完成障碍物的识别与定位。第1次单障碍物避障试验障碍物位置为(−0.125,4.820),第2次单障碍物避障试验障碍物位置为(−0.125,6.820),RZ均为0.45。双障碍物避障试验障碍物位置分别为(0.800,2.500)、(−0.200,5.800),RZ= 0.50。
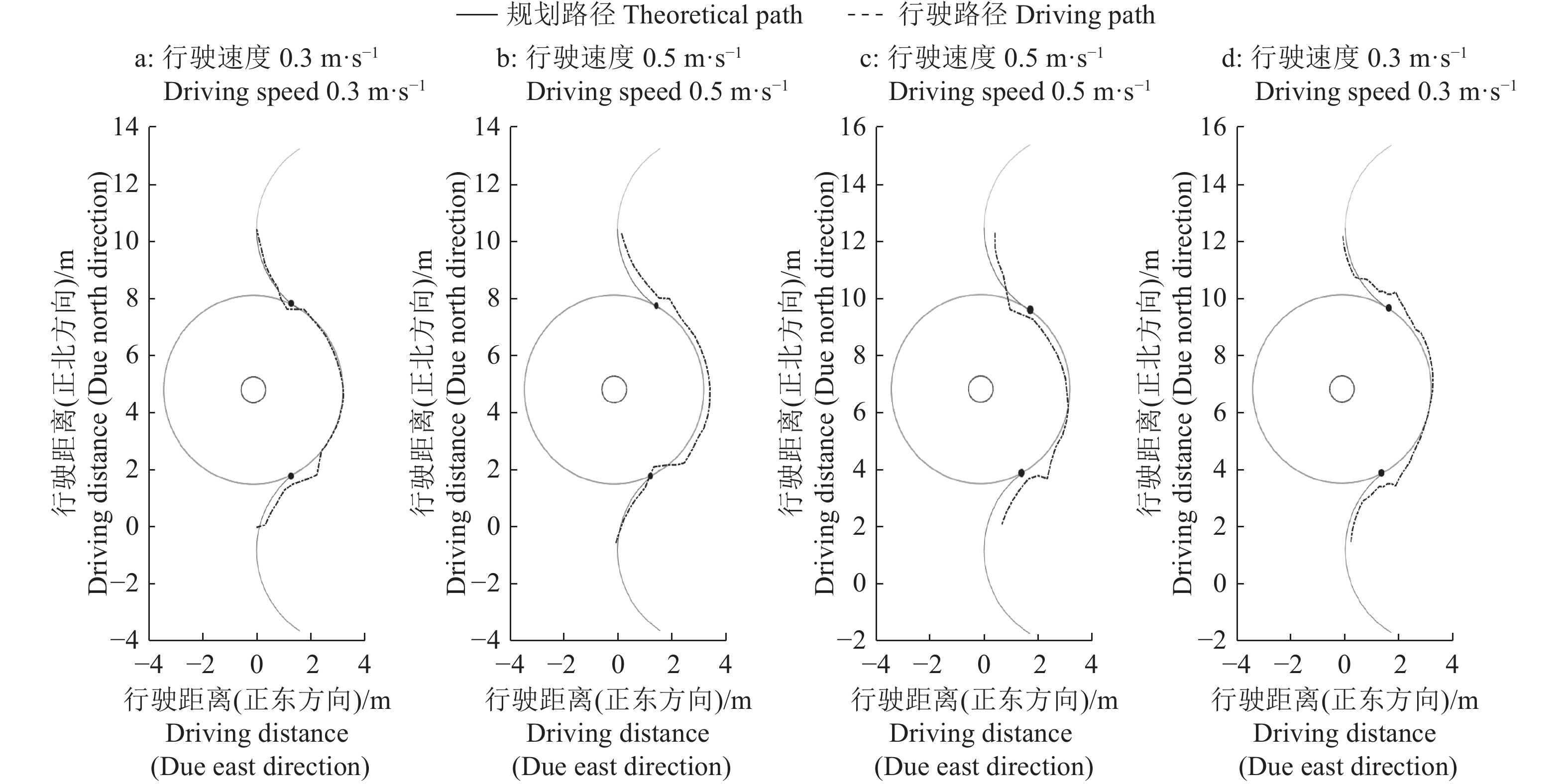
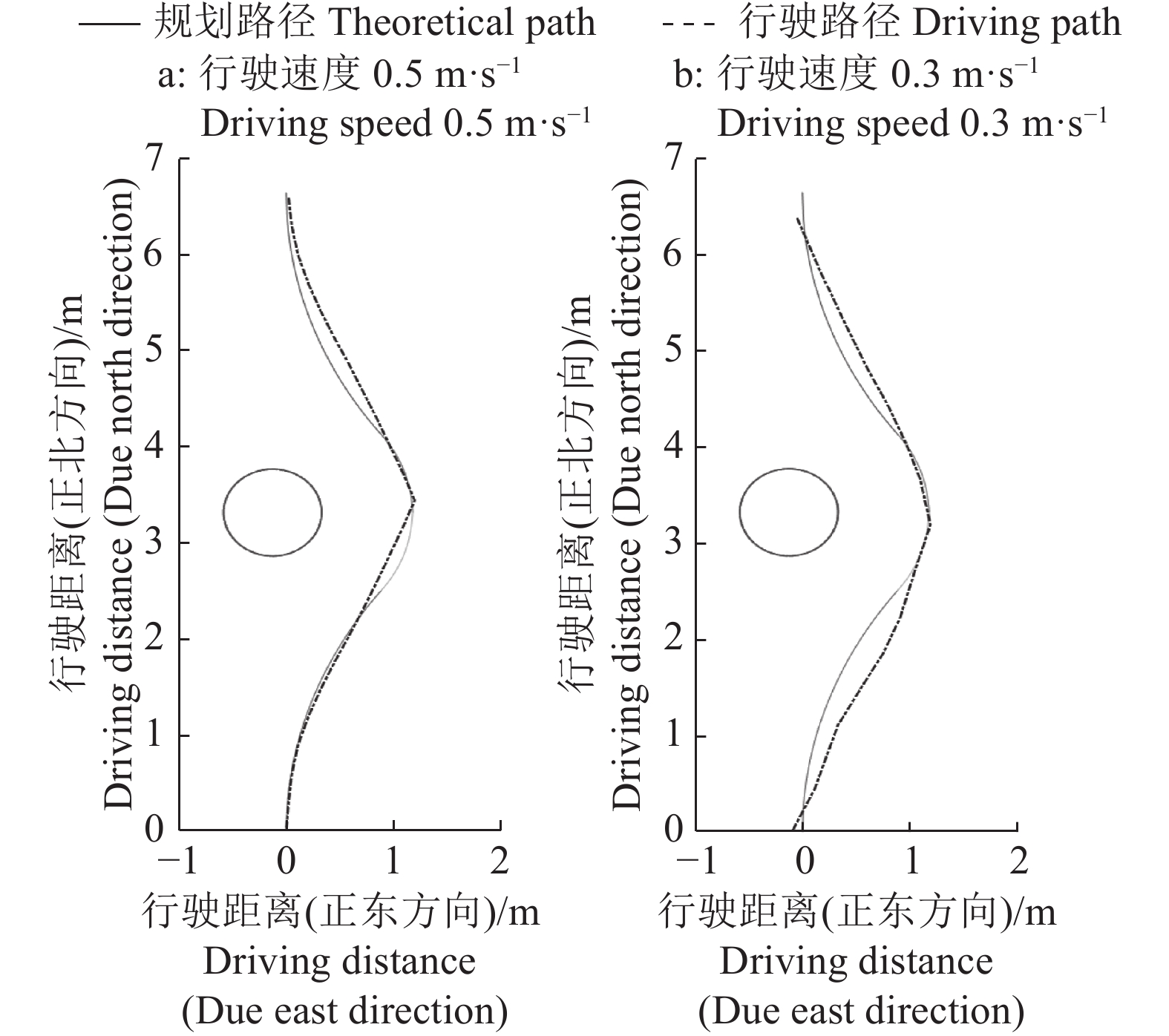
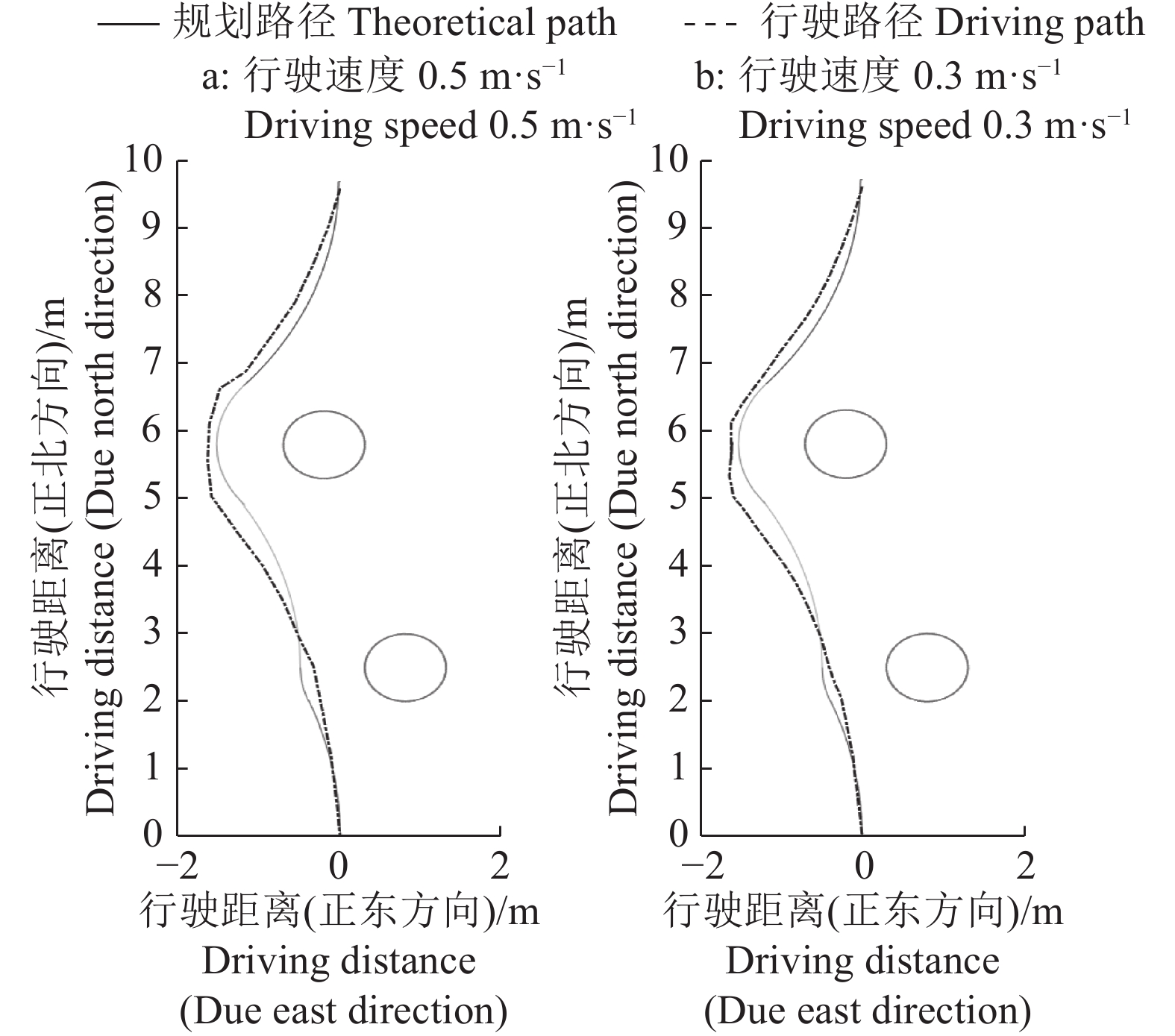
2.2 结果与分析拖拉机分别以0.3、0.5 m·s−1的恒定速度进行试验。单障碍物避障试验结果如图7、图8所示,双障碍物避障试验结果如图9所示。图7表示单个障碍物在不同位置,拖拉机以不同速度跟踪L算法规划的路径时,行驶路径与规划路径的偏差。图8表示在与图7相同条件下,拖拉机以不同速度跟踪单障碍物避障算法规划的路径时,行驶路径与规划路径的偏差。试验中采用0.5 m作为间隔对安全距离区间进行分段,不同速度下2组单障碍物避障试验规划的第1段路径均为行驶的安全距离,仅在距离长短上存在差异。当障碍物位置为(−0.125,4.820)时,拖拉机行驶的安全距离为1.5 m,当障碍物位置为(−0.125,6.820)时,拖拉机行驶的安全距离为3.5 m。因此最终试验结果以行驶dn后的起始避障点作为原点,更新障碍物坐标后,2组试验障碍物的位置坐标相对拖拉机当前位置均为(−0.125,3.320)。根据障碍物位置2组试验采用相同的4段圆弧避障策略,最终不同速度下2组避障试验中拖拉机行驶路径与规划路径差异很小(图8)。图9表示在双障碍物条件下拖拉机以不同速度跟踪双/多障碍物避障算法规划路径时,行驶路径与规划路径的偏差。
|
图 7 单障碍物和不同行驶速度条件下L算法避障试验 Fig. 7 Obstacle avoidance experiments of L algorithm at single obstacle and different driving speeds conditions |
|
图 8 单障碍物和不同行驶速度条件下单障碍物避障算法避障试验 Fig. 8 Obstacle avoidance experiments of single obstacle avoidance algorithm at single obstacle and different driving speeds conditions |
|
图 9 双障碍物和不同行驶速度条件下双/多障碍物避障算法避障试验 Fig. 9 Obstacle avoidance experiments of double/multiple obstacles avoidance algorithm at double obstacles and different driving speeds conditions |
表1定量分析了在单障碍物和不同行驶速度条件下,单障碍物避障算法与L算法规划路径和行驶路径的差别。通过行驶路径累计误差与方差的对比,反映2个算法在实际应用时稳定性与实用性的差别。
|
|
表 1 单障碍物和不同行驶速度条件下单障碍物避障算法与L算法对比 Table 1 Contrast of single obstacle avoidance algorithm and L algorithm at single obstacle and different driving speeds conditoins |
当障碍物位于(−0.125,4.820)时,单障碍物避障算法规划路径比L算法减少32%。试验中当拖拉机行驶速度以0.3、0.5 m·s−1时跟踪单障碍物避障算法规划路径时行驶路径比L算法分别减少35%、38%,行驶路径累计误差分别减少53%、66%。
当障碍物位置位于(−0.125,6.820)时,单障碍物避障算法规划路径比L算法减少26%。试验中当拖拉机行驶速度以0.3、0.5 m·s−1时跟踪单障碍物避障算法规划路径时,行驶路径比L算法分别减少26%、22%,行驶路径累计误差分别减少82%、62%。
由表2可知,双/多障碍物避障算法规划路径为10.29 m,试验中当拖拉机行驶速度为0.3、0.5 m·s−1时,跟踪双/多障碍物避障算法行驶路径为10.30、10.36 m,与规划路径相比仅分别增加0.09%、0.6%,跟踪双/多障碍物避障算法规划路径的行驶路径累计误差为9.99、4.13 m。
|
|
表 2 双/多障碍物避障算法试验数据分析 Table 2 Data analyses of double/multiple obstacles avoidance algorithm experiments at double obstacles and different driving speeds conditions |
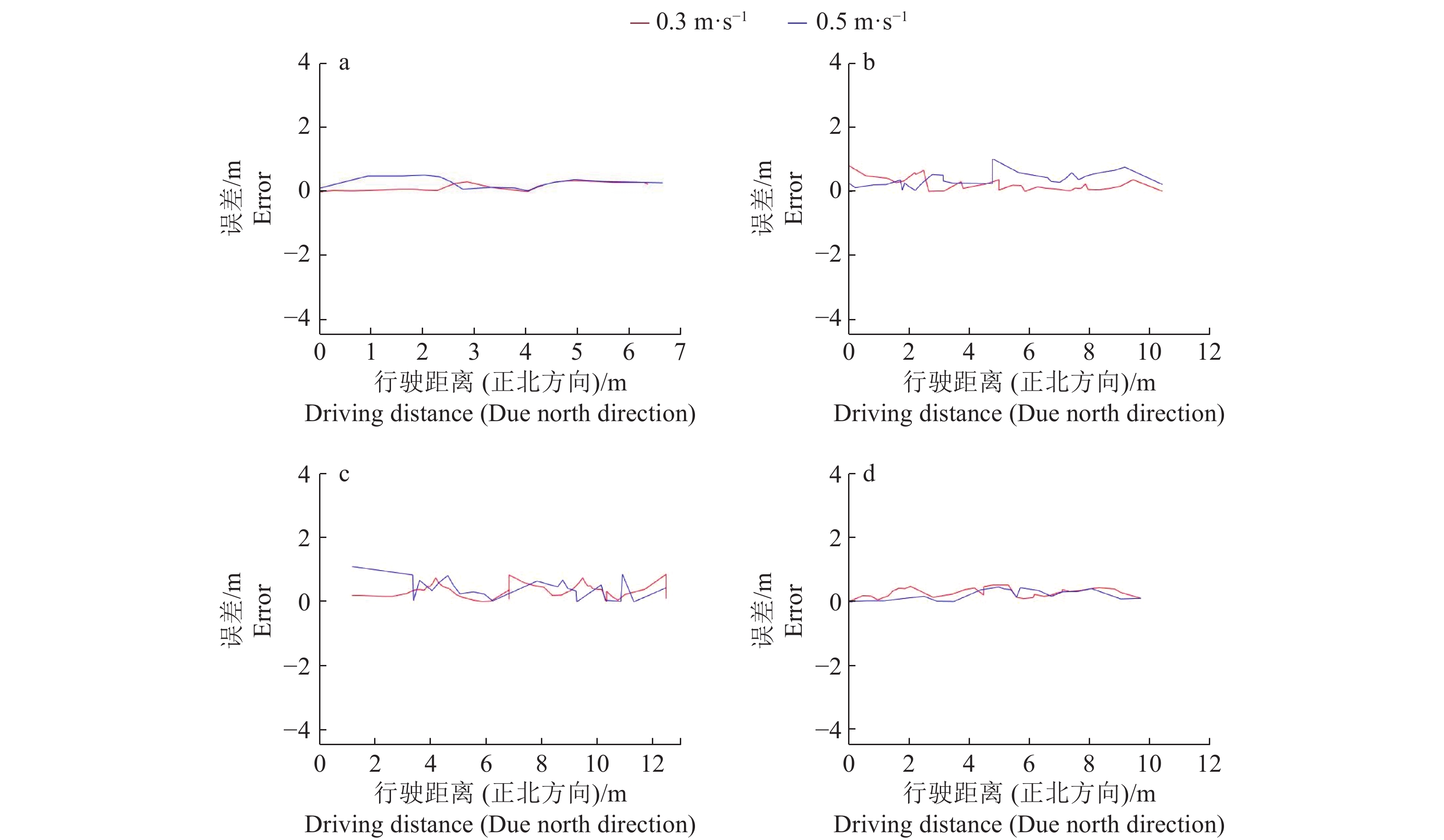
图10表示4组试验中由GPS定位数据计算得到的多点误差值,图 10a表示当障碍物位置为(−0.125,4.820)、(−0.125,6.820)时在单障碍物避障算法下行驶路径与规划路径的误差;图 10b表示当障碍物位置为(−0.125,4.820)时在L算法下行驶路径与规划路径的误差;图 10c表示当障碍物位置为(−0.125,6.820)时在L算法下行驶路径与规划路径的误差;图 10d表示当道路上存在2个障碍物,位置为(−0.200,5.800)、(0.800,2.500)时在双/多障碍物避障算法下行驶路径与规划路径的误差。对应的方差值可参照表1、表2,在相同行驶条件下,跟踪单障碍物避障算法规划路径获得的方差值均小于L算法。
|
图 10 不同障碍物条件下以不同行驶速度跟踪不同算法避障路径时行驶路径与规划路径的误差 Fig. 10 Errors between driving path and theoretical path caused by tracking obstacle avoidance paths of different algrithms at the different obstacle conditions and driving speeds a:单障碍物避障算法,障碍物位置为(−0.125,4.820)、(−0.125,6.820);b:L算法,障碍物位置为(−0.125,4.820);c:L算法,障碍物位置为(−0.125,6.820);d:双/多障碍物算法,2个障碍物位置为(−0.200,5.800)、(0.800,2.500) a: Single obstacle avoidance algorithm, the locations of the obstacle were (−0.125, 4.820) and (−0.125, 6.820); b: L algorithm, the location of the obstacle was (−0.125, 4.820); c: L algorithm, the location of the obstacle was (−0.125, 6.820); d: Double/multiple obstacles avoidance algorithm, the locations of two obstacles were (−0.200, 5.800) and (0.800, 2.500) |
1)单障碍物避障算法的规划路径与L算法相比大幅减少,障碍物在不同位置下减幅达32%、26%。
2)算法投入实际应用中,由单障碍物避障试验4组数据可得,行驶路径平均减少30%,行驶路径累计误差平均减少65%。
3) L算法在试验过程中出现了算法起始避障点超过拖拉机当前位置点的情况,导致拖拉机无法完整跟踪避障路径。本文算法很好地规避了这个问题,首先利用避障安全距离尽可能地贴近障碍物,再采用避障策略完成避障动作。若拖拉机当前位置过于贴近障碍物,算法会提示拖拉机停止工作,否则会有与障碍物碰撞的风险。
4)由统计误差的方差可知,无论拖拉机行驶速度快或慢,跟踪本文算法避障路径的稳定性更好,基于拖拉机运动模型建立的避障策略更圆滑,很少出现L算法中拖拉机大幅偏离行驶路径的情况。除此之外,本文算法解决了现阶段2个障碍物相隔距离较短时拖拉机无法完成避障的问题。
| [1] |
姬长英, 周俊. 农业机械导航技术发展分析[J]. 农业机械学报, 2014, 45(9): 44-54. DOI:10.6041/j.issn.1000-1298.2014.09.008 (  0) 0) |
| [2] |
GAN-MOR S, CLARK R L, UPCHURCH B L. Implement lateral position accuracy under RTK-GPS tractor guidance[J]. Comput Electron Agric, 2007, 59(1/2): 31-38. (  0) 0) |
| [3] |
TIMO O, JUHA B. Guidance system for agricultural tractor with four wheel steering[J]. IFAC Proceed Vol, 2013, 46(4): 124-129. DOI:10.3182/20130327-3-JP-3017.00030 (  0) 0) |
| [4] |
KARIMI D, HENRY J, MANN D D. Effect of using GPS autosteer guidance systems on the eye-glance behavior and posture of tractor operators[J]. J Agric Saf Health, 2012, 18(4): 309-318. DOI:10.13031/2013.42332 (  0) 0) |
| [5] |
刘柯楠, 吴普特, 朱德兰, 等. 太阳能渠道式喷灌机自主导航研究[J]. 农业机械学报, 2016, 47(9): 141-146. DOI:10.6041/j.issn.1000-1298.2016.09.021 (  0) 0) |
| [6] |
CORDESSES L, CARIOU C, BERDUCAT M. Combine harvester control using real time kinematic GPS[J]. Precis Agric, 2000, 2(2): 147-161. DOI:10.1023/A:1011473630247 (  0) 0) |
| [7] |
CHOI J, YIN X, YANG L, et al. Development of a laser scanner-based navigation system for a combine harvester[J]. E A Environment F, 2014, 7(1): 7-13. DOI:10.1016/j.eaef.2013.12.002 (  0) 0) |
| [8] |
张美娜, 吕晓兰, 陶建平, 等. 农用车辆自主导航控制系统设计与试验[J]. 农业机械学报, 2016, 47(7): 42-47. DOI:10.6041/j.issn.1000-1298.2016.07.007 (  0) 0) |
| [9] |
张漫, 项明, 魏爽, 等. 玉米中耕除草复合导航系统设计与试验[J]. 农业机械学报, 2015, 46(S1): 8-14. DOI:10.6041/j.issn.1000-1298.2015.S0.002 (  0) 0) |
| [10] |
谢斌, 李静静, 鲁倩倩, 等. 联合收割机制动系统虚拟样机仿真及试验[J]. 农业工程学报, 2014, 30(4): 18-24. DOI:10.3969/j.issn.1002-6819.2014.04.003 (  0) 0) |
| [11] |
任述光, 谢方平, 王修善, 等. 4LZ-0.8型水稻联合收割机清选装置气固两相分离作业机理[J]. 农业工程学报, 2015, 31(12): 16-22. DOI:10.11975/j.issn.1002-6819.2015.12.003 (  0) 0) |
| [12] |
焦有宙, 田超超, 贺超, 等. 不同工质对大型联合收割机余热回收的热力学性能[J]. 农业工程学报, 2018, 34(5): 32-38. DOI:10.11975/j.issn.1002-6819.2018.05.005 (  0) 0) |
| [13] |
伟利国, 张小超, 汪凤珠, 等. 联合收割机稻麦收获边界激光在线识别系统设计与试验[J]. 农业工程学报, 2017, 33(S1): 30-35. (  0) 0) |
| [14] |
刘刚, 李笑, 康熙, 等. 基于GNSS的农田平整自动导航路径规划方法[J]. 农业机械学报, 2016, 47(S1): 21-29. (  0) 0) |
| [15] |
孟志军, 刘卉, 王华, 等. 农田作业机械路径优化方法[J]. 农业机械学报, 2012, 43(6): 147-152. DOI:10.6041/j.issn.1000-1298.2012.06.027 (  0) 0) |
| [16] |
TAÏX M, SOUÈRES P, FRAYSSINET H, et al. Path planning for complete coverage with agricultural machines[M]//Springer-verlag Berlin. Springer tracts in advanced robotics. Berlin: Springer-verlag, 2006.
(  0) 0) |
| [17] |
KANG N K, SON H J, LEE S H. Modified A-star algorithm for modular plant land transportation[J]. J Mech Sci Technol, 2018, 32(12): 5563-5571. DOI:10.1007/s12206-018-1102-z (  0) 0) |
| [18] |
LE A V, PRABAKARANV, SIVANANTHAMV, et al. Modified A-star algorithm for efficient coverage path planning in tetris inspired self-reconfigurable robot with integrated laser sensor[J]. Sensors, 2018, 18(8). doi: 10.3390/s18082585.
(  0) 0) |
| [19] |
吴麟麟, 杨俊辉, 汪若尘, 等. 基于混合SA算法的智能汽车全局路径规划[J]. 江苏大学学报(自然科学版), 2019, 40(3): 249-254. DOI:10.3969/j.issn.1671-7775.2019.03.001 (  0) 0) |
| [20] |
刘建华, 杨建国, 刘华平, 等. 基于势场蚁群算法的移动机器人全局路径规划方法[J]. 农业机械学报, 2015, 46(9): 18-27. DOI:10.6041/j.issn.1000-1298.2015.09.003 (  0) 0) |
| [21] |
陈余庆, 李桐训, 于双, 等. 基于势场蚁群算法的机器人全局路径规划[J]. 大连理工大学学报, 2019, 59(3): 316-322. DOI:10.7511/dllgxb201903014 (  0) 0) |
| [22] |
谢永良, 尹建军, 余承超, 等. 轮式AGV沿葡萄园垄道行驶避障导航算法与模拟试验[J]. 农业机械学报, 2018, 49(7): 13-22. DOI:10.6041/j.issn.1000-1298.2018.07.002 (  0) 0) |
| [23] |
殷建军, 董文龙, 梁利华, 等. 复杂环境下农业机器人路径规划优化方法[J]. 农业机械学报, 2019, 50(5): 17-22. DOI:10.6041/j.issn.1000-1298.2019.05.002 (  0) 0) |
| [24] |
TIAN L F, COLLINS C. An effective robot trajectory planning method using a genetic algorithm[J]. Mechatronics, 2003, 14(5): 455-470. (  0) 0) |
| [25] |
KIM H, KIM B K. Online minimum-energy trajectory planning and control on a straight-line path for three-wheeled omnidirectional mobile robots[J]. IEEE T Ind Electron, 2014, 61(9): 4771-4779. DOI:10.1109/TIE.2013.2293706 (  0) 0) |
| [26] |
GREGORY J, OLIVARES A, STAFFETTI E. Energy-optimal trajectory planning for robot manipulators with holonomic constraints[J]. Syst Control Lett, 2012, 61(2): 279-291. DOI:10.1016/j.sysconle.2011.11.005 (  0) 0) |
| [27] |
LIU C, ZHAO X, DU Y. Research on the static path planning method of small obstacles for automatic navigation of agricultural machinery[C]. IFAC-Papers. Beijing. 2018: 673-677.
(  0) 0) |
 2020, Vol. 41
2020, Vol. 41


