2. 山东理工大学 农业工程与食品科学学院,山东 淄博 255000
2. School of Agricultural Engineering and Food Science, Shandong University of Technology, Zibo 255000, China
随着农业现代化的发展,农业机器人等智能化农业设备得到了越来越广泛地应用,而路径规划在农业机器人应用过程中起着至关重要的作用。路径规划一般分为环境地图完全已知的静态路径规划和环境地图部分已知或全部未知的动态路径规划[1]。对于静态路径规划,一种是传统的点到点的路径规划,另一种是完全遍历路径规划[2]。点到点的路径规划要求寻找一条从始点到终点的最优路径,路径代价最小、距离最短、时间最少[3],使农业机器人能够在工作空间顺利通行而不碰到任何障碍物。完全遍历路径规划是一种在满足某种性能指标最优的前提下,在设定区域内寻找一条从始点到终点且经过所有可达区域的连续路径[4]。
针对农业机器人的需求,其路径规划主要是完全遍历路径规划。采用模拟退火算法进行完全遍历路径规划能够以一定概率跳出局部最优解从而趋于全局最优[5],但无法保证在终止于停止准则时所获得的最终解一定是最优解,甚至无法保证最终解是整个搜索过程中曾经获得过的最优解[6]。本文提出一种基于记忆模拟退火和A*算法的遍历路径规划算法,通过记忆模拟退火算法搜索出最优任务目标点的行走顺序,然后使用A*算法进行跨区域衔接路径规划,从而实现农业机器人遍历路径规划。
1 环境建模 1.1 建立栅格地图本文采用栅格法[7]进行环境建模,将农业机器人工作环境分解成一系列具有二值信息的网络单元,单元格大小以农业机器人尺寸为准。然后给每个栅格赋予环境信息值:若其中某个栅格范围内不含有任何障碍物,则称此栅格为自由栅格,反之称为障碍栅格。环境信息赋予完成后,则相当于把工作环境地图离散化[8],每个单元格映射为环境信息的一部分,具体如图1所示。

|
图 1 栅格地图 Fig. 1 Grid map |
栅格地图中不仅存在和栅格单元边缘完全重合的规则障碍物,还存在一些不能和栅格单元边界完全重合的不规则障碍物。需要采用二值形态学中的膨胀运算对不规则障碍物进行膨胀处理,使其边缘能够完全和单元栅格边界重合。这样可以有效避免农业机器人陷入死角以及智能算法陷入局部最优[9],减少路径规划的重复率,为农业机器人完全遍历路径规划做好准备。
膨胀运算的数学模型如式1所示,其中A是被膨胀的元素集合,B是一个结构元素,
| $S = A \oplus B = \left\{ {\left( {x,y} \right)|{{\hat B}_{{\rm{xy}}}} \cap A \ne \emptyset } \right\}{\text{,}}$ | (1) |
式中,
根据上述膨胀数学模型,选择栅格单元元素为结构元素B,对不规则障碍物的边缘区域进行膨胀处理,结果如图2所示。

|
图 2 障碍物膨胀处理 Fig. 2 Obstacle expansion treatment |
建立二维栅格地图后,由于障碍物分布毫无规律,农业机器人会产生工作效率低、遍历不完全、重复率高等问题。为简化流程,可以将其划分为若干个子问题,即将整个二维栅格地图划分为若干个不包含障碍物的矩形子区域,使农业机器人先在矩形子区域内进行遍历路径规划,然后经过分区重组达到全覆盖遍历路径规划。
划分矩形子区域时,先在栅格地图左下角建立直角坐标系作为标识,然后根据障碍物进行矩形子区域划分,并尽量使矩形子区域面积达到最大值。首先确定障碍物栅格最右下角的点,记为k,然后过k点分别画平行于x轴的横向分割线和平行于y轴的纵向分割线,分割线以点k为中心分别向两边延伸,直至遇到栅格边缘、障碍物或另一条分割线时停止。重复以上步骤,直至将整个栅格地图完全划分为若干个矩形子区域。
矩形子区域划分完成后,根据矩形最大化原则将矩形子区域合并,这样就可以进一步减少矩形子区域的个数,同时减少因跨区域产生的重复路径,提高农业机器人路径规划的效率。矩形子区域合并完成后,将其按照从上到下、从左到右的原则进行标号,这样有利于之后的遍历顺序安排,最终结果如图3所示。
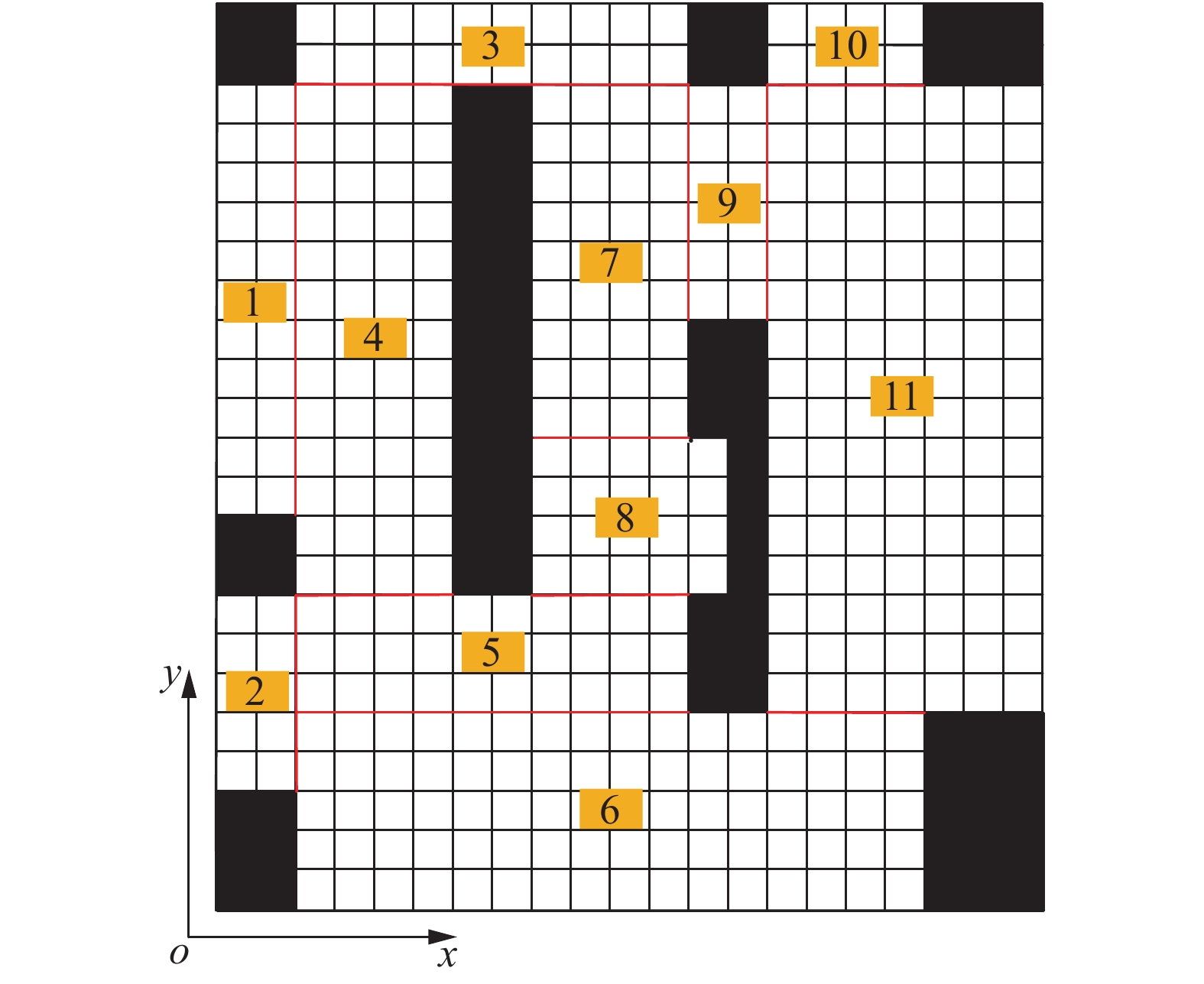
|
图 3 矩形子区域划分结果 Fig. 3 Result of rectangular sub-region division 图中数字为标号 The figures in the diagram are labels |
划分矩形子区域后,农业机器人在单个矩形子区域内完成遍历工作后,需要根据所有分区遍历的先后顺序,从当前矩形子区域进入到下一个工作区域。在这2个跨区域的矩形子区域衔接路径规划中,为了降低遍历路径的重复率,提高整体效率,采用具有启发式搜索功能的A*算法[10]进行最短路径规划,实现从上一个矩形子区域遍历终点到下一个矩形子区域遍历起点的最短路径的规划。
2.1 建立评价函数A*算法作为一种启发式路径搜索规划算法,在路径规划过程中加入评价函数对候选节点进行评估,以栅格地图上从起始点经过当前候选节点到达目标点的代价为根据决定搜索方向,选择具有最小代价的节点进行扩展,直至搜索到目标节点为止[11],则其走过的路径即为最优路径。
A*算法将从起始点到当前点的评价函数和从当前点到目标点的评价函数结合起来形成从起始点到目标点的评价函数[12]。其数学表达式为:
| $f\left( n \right) = g\left( n \right) + h\left( n \right),$ | (2) |
式中,f(n)表示从起始点到目标点的评价函数,g(n)表示从起始点到当前点n的实际代价函数,h(n)表示从当前点n到目标点的启发代价函数。
其中,启发代价函数h(n)的引入能够使当前位置始终优先向目标点移动,以达到先筛除冗余的无用解的目的。常用的启发代价函数有曼哈顿距离、欧式距离[13]等。虽然欧式距离能够实现两点之间最短距离的求解,但在栅格地图中采用欧式距离往往不符合实际情况,故采用曼哈顿距离作为启发函数。其数学表达式如下:
| $h\left( n \right) = |{x_{{n}}} - {x_{{\rm{goal}}}}| + |{y_{{n}}} - {y_{{\rm{goal}}}}|,$ | (3) |
式中,xn、yn分别为当前节点的横、纵坐标,xgoal、ygoal分别为目标点的横、纵坐标。
2.2 A*算法仿真试验以图3栅格地图中部分矩形子区域为例,假设农业机器人从A点走到B点,但是两点之间被障碍物分隔。通过A*算法对两点之间进行如图4所示的路径搜索。

|
图 4 农业机器人A*算法路径搜索 Fig. 4 Path search of agricultural robot by A* algorithm 红色圆点即从起点A到目标点B的最短路径;方格中左上角数字为 f 值,代表由起点A到目标点B的代价值;右下角数字为 h 值,代表从指定节点到终点B的估算成本;左下角数字为 g 值,代表农业机器人从起点A移动到指定节点的移动代价 The red dots are the shortest path from starting point A to target point B; The upper left number is f value, representing the cost value for moving from starting point A to target point B; The bottom right number is h value, representing the estimated cost for moving from an assigned node to target point B; The bottom left number is g value, representing the movement cost for moving from starting point A to an assigned node |
采用八邻域法进行邻域扩展,即农业机器人在父节点时可同时搜索相邻8个候选节点。本研究中,横向和纵向移动代价设为10,对角线的移动代价设为14,栅格中指针指向的是它们的父节点。为避免农业机器人因自身体积原因碰到障碍物栅格而无法继续前进甚至损坏农业机器人,在经过障碍物转角的时候使其沿障碍物转角直线转弯而不是直接穿过障碍物转角。
3 矩形子区域遍历顺序规划为实现农业机器人遍历路径规划,减少遍历重复率,则需要保证每个矩形子区域在全局遍历路径规划中有且仅被规划1次,可以转化为求解旅行商问题(Traveling salesman problem,TSP),TSP求解的最短路径对应矩形子区域的最优遍历顺序。而模拟退火算法在搜索最优遍历顺序的时候,能够以一定的概率接受1个比当前解更差的解,从而跳出局部最优解,最终趋于全局最优[14]。本研究在传统模拟退火算法的基础上,采用记忆模拟退火算法记录当前最优解,防止在跳出局部最优解的同时丢失全局最优解。
3.1 建立矩形子区域基点图为便于矩形子区域遍历顺序规划,以矩形子区域中心基点代表整个矩形子区域,并用坐标等参数来表明各个矩形子区域在环境中的具体位置,如图5所示。
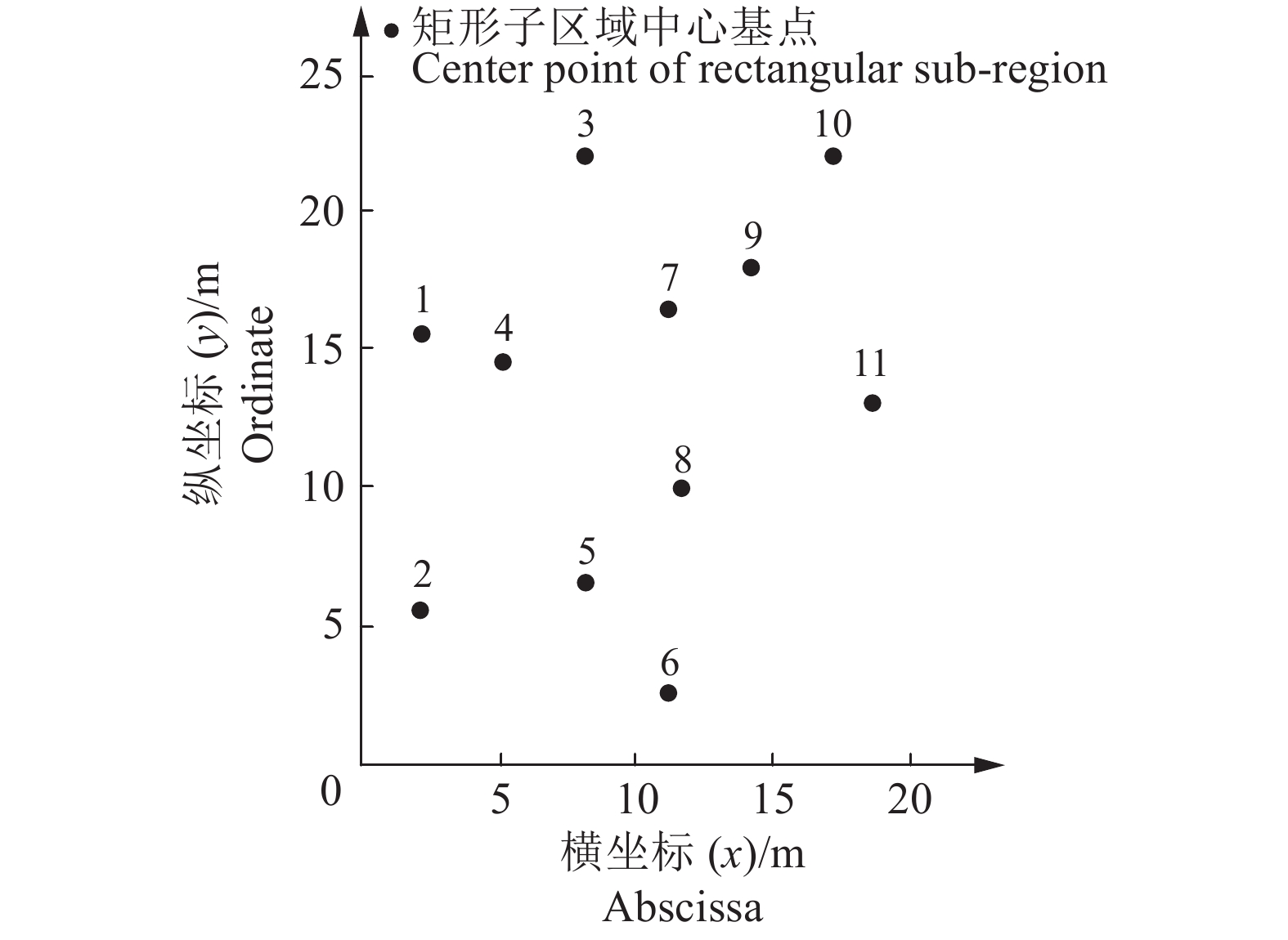
|
图 5 矩形子区域基点图 Fig. 5 Base point plot of rectangular sub-region |
矩形子区域遍历顺序规划即转化为采用记忆模拟退火算法搜索经过每个基点且每个基点只经过1次的最短路径。在进行遍历顺序规划时,考虑到各矩形子区域间的连通关系、障碍物情况,在定义两基点之间的距离时,以上一个矩形子区域遍历终点到下一个矩形子区域遍历起点的曼哈顿距离来表示2个基点之间的实际距离,使其更加符合栅格地图中农业机器人的实际运动情况。
综上所述,各个基点的距离矩阵如下所示:
| $D = \left[ {\begin{array}{*{20}{c}} {{d_{1,1}}}&{{d_{1,2}}}&{{d_{1,3}}}& \cdots &{{d_{1,11}}} \\ {{d_{2,1}}}&{{d_{2,2}}}&{{d_{2,3}}}& \ldots &{{d_{2,11}}} \\ {{d_{3,1}}}&{{d_{3,2}}}&{{d_{3,3}}}& \cdots &{{d_{3,11}}} \\ \vdots & \vdots & \vdots & \ddots &{} \\ {{d_{11,1}}}&{{d_{11,2}}}&{{d_{11,3}}}&{}&{{d_{11,11}}} \end{array}} \right],$ | (4) |
其中,
模拟退火算法是一种强大的启发式全局搜索算法,已在理论上被证明是一种以概率1收敛于全局最优解的全局优化算法[15],其通过模拟固体退火过程,采用冷却进度表控制算法进程,并引入Metropolis准则,使算法能够通过“概率判断”跳出局部最优解从而趋于全局最优。但“概率判断”可能会使算法忽略掉当前的最优解,无法保证在终止于停止准则时所得的最终解一定是最优解,甚至无法保证最终解是整个搜索过程中曾经达到的最优解。
基于上述事实,本研究决定给传统模拟退火算法增加一个记忆器,使之能够记住搜索过程中遇到过的最优解,当退火过程结束后,将所得到的最终解与记忆器中的解进行比较并取较优解作为最终结果,从而提高算法所得解的质量。
在本文实例中,解空间S为解的所有排列顺序的集合,其表示如下:
S={(s1,…,s11)| (s1,…,s11)为矩形子区域{1,···,11}的循环排列}。
对解空间进行简单变换即可产生新解,其变换方法通常有2变换法和3变换法。
2变换法任选序号u和v(设u<v),逆转u和v及其之间的访问顺序,记为swap2(u,v)。
若初始状态序列为:s1…su−1susu+1…sv−1svsv+1…s11,
采用2变换法变换后的状态序列为:s1…su−1svsv−1…su+1susv+1…s11。
3变换法任选序号u、v和w(设u<v<w),将u和v之间的路径插到w之后访问,记为swap3(u,v,w)。
若初始状态序列为:s1…su−1susu+1…sv−1svsv+1…sw−1swsw+1…s11,则采用3变换法变换后的状态序列为:s1…su−1sv+1…swsu…svsw+1…s11。
这2种变换方法各有其独特的优越性,本文根据其不同特点,将这2种变换方法综合进行使用,根据公式(5),选择其中最优的一个状态作为新解状态。
| $ S = {\rm{min}}\left[ {{\rm{swap}}2\left( {u,v} \right),{\rm{ swap}}3\left( {u,v,w} \right)} \right]{\text{。}} $ | (5) |
在上述新解状态产生函数的基础上,在模拟退火算法中设置2个变量s*和f*,其中s*用于记忆当前遇到的最优解,f*为其目标函数值。开始时令s*和f*分别等于初始解s0及其目标函数值f0;以后每接受1个新解时,就将新解的目标函数值f与f*比较,若f优于f*,则将s和f分别存入s*和f*;最后算法结束时,再从最后的当前解s和s*中选取较优者作为最终解,从而实现模拟退火算法的记忆功能。
为控制算法进程,记忆模拟退火算法采用了1组冷却进度表参数,使其能够在有限时间执行过程后逼近其渐进收敛状态。冷却进度表的相关参数主要包括控制参数(T)的初始值(T0);T的衰减函数:Tk+1=αTk;Mapkob链的长度(L);停止准则:在s个相继的Mapkob链中解无任何变化就终止算法。
根据本研究实例,各控制参数取值分别为T0=100,α=0.98,s=1,L=100n,其中n为问题规模。
3.3 遍历顺序规划仿真试验为验证农业机器人在记忆模拟退火算法下的遍历顺序规划效果,通过MATLAB仿真软件将其与传统模拟退火算法进行比较。图6a为采用传统模拟退火算法的遍历顺序规划图,图6b为采用记忆模拟退火算法的遍历路径规划图。表1为农业机器人在2种算法下的遍历顺序和曼哈顿距离对比。
|
|
表 1 算法遍历顺序规划对比 Table 1 Comparison of traversal sequence planning in different algorithm |
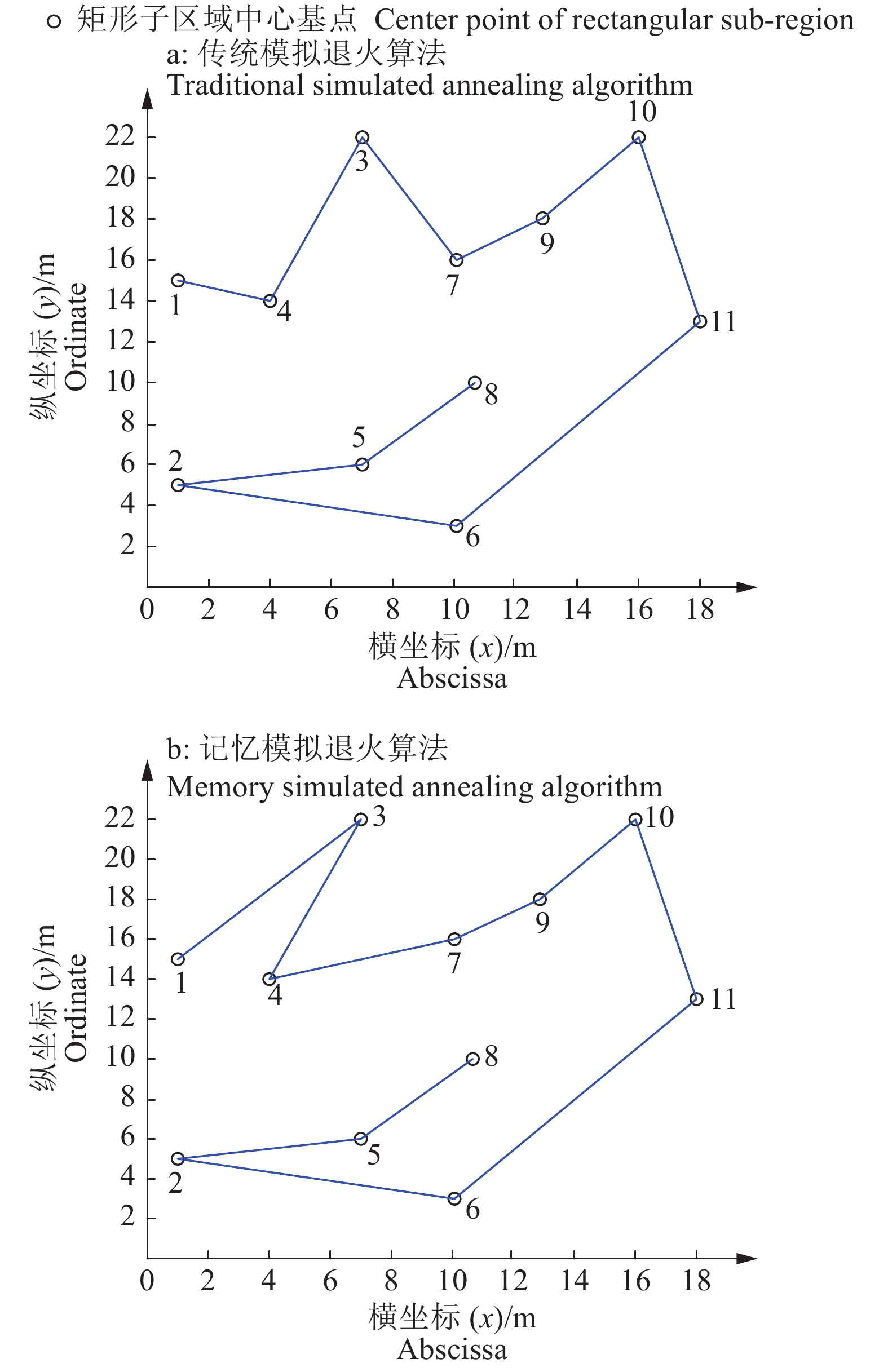
|
图 6 遍历顺序规划图 Fig. 6 Traversal sequence plan |
为便于分析,以图5所示矩形子区域基点坐标图作为环境地图,然后采用曼哈顿距离作为各基点间的距离以表示其连通关系。通过图6和表1可以看出,采用记忆模拟退火算法进行遍历顺序规划增强了算法跳出局部最优陷阱的能力,提高解的质量。实例中采用记忆模拟退火算法所规划的遍历路径曼哈顿距离比传统模拟退火算法减少了9.4%。
4 遍历路径规划仿真通过使用记忆模拟退火算法搜索出最优的任务目标点遍历顺序,使农业机器人能够以最小的移动耗费遍历所有目标点;同时使用A*算法进行跨区域衔接路径规划,搜索出目标点间的最短、无碰撞行走路径。在各矩形子区域内,选取离上一个矩形子区域的终点最近的分区顶点作为这个矩形子区域的起点,然后沿着长边进行“往返式”遍历规划,最终实现对整个栅格地图的遍历路径规划。
通过上述算法,得到的环境案例遍历路径规划如图7所示。由图7可知,整个栅格地图一共由483个栅格组成,其中黑色障碍物所占据的栅格为81个,则自由栅格一共有402个,遍历路径规划覆盖率接近100%。其中重复遍历栅格为17个,遍历路径重复率为4.2%。

|
图 7 遍历路径规划图 Fig. 7 Traversal path planning 绿色圆点和红色五角星分别为整个遍历路径规划的起点和终点,蓝色线条为遍历规划路线 The green dot is the starting point and the red pentagram is the ending point of the whole planned traversal path, the blue line is the planned traversal path |
针对栅格地图中矩形子区域遍历顺序规划,采用记忆模拟退火算法。通过为传统模拟退火算法增加记忆器,使之增强了跳出局部最优陷阱的能力,提高了算法所得解的质量。MATLAB仿真试验表明,采用记忆模拟退火算法所规划的遍历路径曼哈顿距离比传统模拟退火算法减少了9.4%。
针对农业机器人遍历路径规划,提出了一种记忆模拟退火与A*算法相结合的遍历算法。通过记忆模拟退火算法搜索出最优任务目标点行走顺序,然后使用A*算法进行跨区域衔接路径规划。通过仿真试验表明,遍历路径覆盖率接近100%,重复率约为4.2%。
| [1] |
朱铁欣, 董桂菊, 颜丙学, 等. 基于改进蚁群算法的农业机器人路径规划研究[J]. 农机化研究, 2016, 38(9): 48-52. DOI:10.3969/j.issn.1003-188X.2016.09.009 (  0) 0) |
| [2] |
邱雪娜, 刘士荣, 宋加涛, 等. 不确定动态环境下移动机器人的完全遍历路径规划[J]. 机器人, 2006(6): 586-592. DOI:10.3321/j.issn:1002-0446.2006.06.007 (  0) 0) |
| [3] |
邱雪娜, 刘士荣, 俞金寿, 等. 移动机器人的完全遍历路径规划: 生物激励与启发式模板方法[J]. 模式识别与人工智能, 2006, 19(1): 122-128. DOI:10.3969/j.issn.1003-6059.2006.01.022 (  0) 0) |
| [4] |
谢斌, 刘士荣, 俞金寿. 基于在线图搜索的移动机器人遍历运动规划[J]. 华东理工大学学报(自然科学版), 2007(4): 551-557. DOI:10.3969/j.issn.1006-3080.2007.04.021 (  0) 0) |
| [5] |
ZOU D X, WANG G G, PAN G, et al. A modified simulated annealing algorithm and an excessive area model for floorplanning using fixed-outline constraints[J]. Front Inform Tech El, 2016, 17(11): 1228-1244. DOI:10.1631/FITEE.1500386 (  0) 0) |
| [6] |
路鹏, 周东岱, 钟绍春, 等. 基于模拟退火算法的计算机自适应测试项目选择方法研究[J]. 计算机应用与软件, 2012, 29(10): 175-179. (  0) 0) |
| [7] |
杜利超, 钱桦, 肖爱平. 路径规划技术及其在大棚作业机器人中的应用[J]. 湖北农业科学, 2010, 49(5): 1205-1208. DOI:10.3969/j.issn.0439-8114.2010.05.058 (  0) 0) |
| [8] |
史兵, 段锁林, 李菊, 等. 温室移动机器人复合栅格地图构建方法研究[J]. 计算机应用研究, 2019, 36(3): 824-828. (  0) 0) |
| [9] |
张堂凯. 己知环境下智能清洁机器人路径规划研究[D]. 南京: 南京邮电大学, 2017.
(  0) 0) |
| [10] |
QIAN J Y, ZHOU Z D, ZHAO L Z, et al. Accelerating reconfiguration for VLSI arrays with A‐star algorithm[J]. IEEJ T Electr Electr, 2018, 13(10): 1511-1519. DOI:10.1002/tee.22716 (  0) 0) |
| [11] |
王维, 裴东, 冯璋. 改进A*算法的移动机器人最短路径规划[J]. 计算机应用, 2018, 38(5): 1523-1526. (  0) 0) |
| [12] |
张欣欣, 薛金林. 基于云模型的农业移动机器人人机合作路径规划[J]. 华南农业大学学报, 2017, 38(6): 105-111. DOI:10.7671/j.issn.1001-411X.2017.06.016 (  0) 0) |
| [13] |
张文, 刘勇, 张超凡, 等. 基于方向A*算法的温室机器人实时路径规划[J]. 农业机械学报, 2017, 48(7): 22-28. DOI:10.6041/j.issn.1000-1298.2017.07.003 (  0) 0) |
| [14] |
孙秀巧, 王健, 巫威眺. 基于改进遗传退火算法的高速公路巡逻车路径优化调度[J]. 科学技术与工程, 2019, 19(21): 296-302. DOI:10.3969/j.issn.1671-1815.2019.21.045 (  0) 0) |
| [15] |
MIAO Z W, YANG F, FU K, et al. Transshipment service through crossdocks with both soft and hard time windows[J]. Ann Oper Res, 2012, 192(1): 21-47. DOI:10.1007/s10479-010-0780-4 (  0) 0) |
 2020, Vol. 41
2020, Vol. 41


