2. 山东理工大学 农业工程与食品科学学院,山东 淄博 255000
2. School of Agricultural Engineering and Food Science, Shandong University of Technology, Zibo 255000, China
数字生态循环农业可解决我国农业发展存在的农药和化肥使用过量及利用率低、劳动力成本昂贵、农业废弃物难处理、生态环境恶化、农产品质量下降等问题,将成为未来农业发展的主流方向[1-2]。实现农业机器人在拥有复杂环境的数字生态循环农业农场中的全区域覆盖是数字农业的研究趋势之一,有利于降低农业机器人在农田中遍历的路径重复率、提高农业机器人的工作效率。
近些年来,国内外学者围绕机器人在工作区域中的全区域覆盖问题展开了大量的研究[3-4],Choi等[5]设计了一种基于内螺旋和限制逆距离转换的在线全覆盖算法;Kapanoglu等[6]将模板法和遗传算法相融合解决机器人的全覆盖路径规划问题;李楷等[7]提出了一种基于回溯法的全覆盖路径规划算法,在通过West-move first算法实现局部区域覆盖的基础上通过改进的A*算法规划出一条从死点到回溯点的光滑无障碍路径;曹翔等[8]使用不同的函数值表示障碍物、已覆盖栅格和未覆盖栅格,引入方向信度函数对栅格信度函数值进行优化并根据栅格信度函数进行遍历路径规划,该方案在环境较复杂的工作区域中遍历时难以保证对工作区域的全覆盖;聂杨[9]将环境地图栅格化并划分子区域,通过机器人依次遍历相邻子区域完成对环境地图的覆盖,但在环境复杂且子区域较多时该方案易引起较大的路径重复率。
本文通过栅格分区的方法简化数字生态农业农场中复杂的工作环境,在此基础上从优化路径重复率的角度出发分别通过改进的蚁群算法和广度优先搜索 (Breadth first search, BFS)算法规划机器人在分区间的遍历顺序与分区间的衔接路径,以此实现农业机器人对农田工作区域的全覆盖。
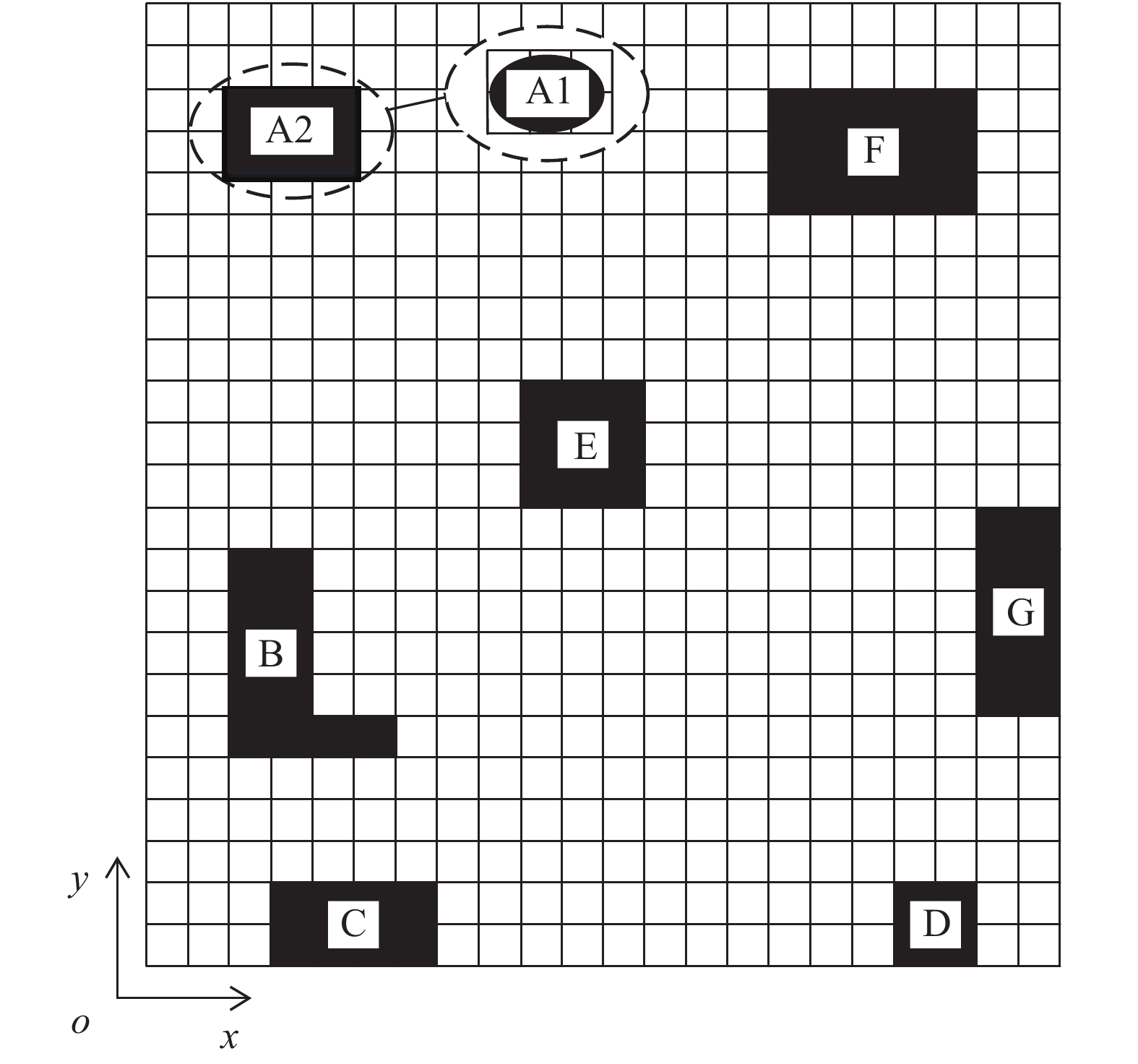
1 栅格化环境建模与矩形分区 1.1 建立栅格地图农田栅格化以及各障碍物膨胀结果如图1所示。农业机器人的工作环境多遍布电线杆、固定安装的传感器等异形障碍物。为减少农业机器人在复杂环境农田中遍历时产生的路径重复率,本文通过栅格法对农场的环境进行建模,并根据农业机器人的工作范围设置栅格图中单元格的单位长度。对障碍物边缘线与栅格边缘线不重合的情况进行膨胀运算,即不满1个单元格的障碍物按1个单元格处理。
|
图 1 栅格地图 Fig. 1 Raster map A1表示膨胀处理前的障碍物;A2表示膨胀处理后的A1;B、C、D、E、F和G表示膨胀处理后的障碍物 A1 represents the obstacle before expansion treatment; A2 represents the A1 after expansion treatment; B, C, D, E, F and G represent obstacles after expansion treatment |
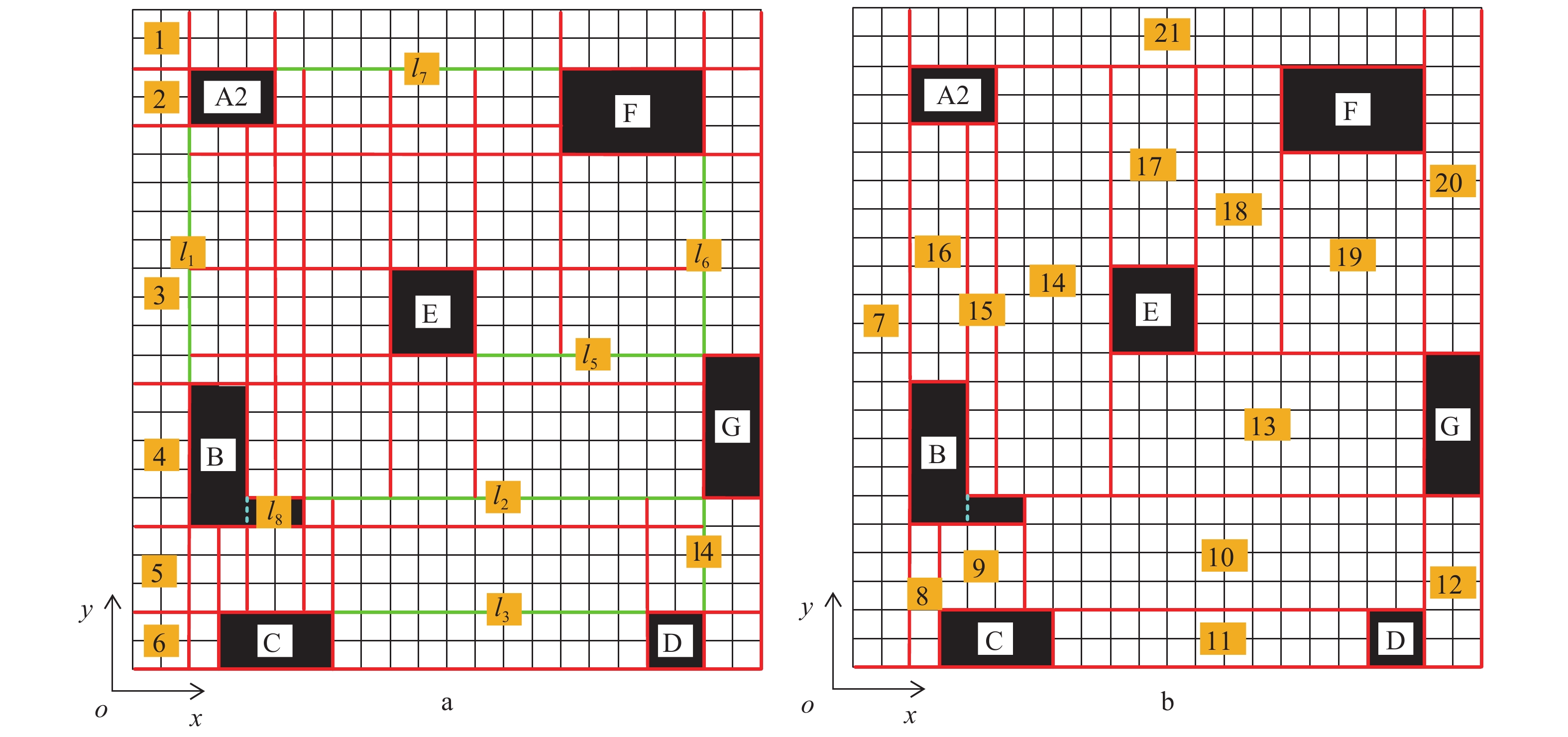
农业机器人在复杂环境农田中遍历时容易遗漏部分工作区域以及出现较高的路径重复率的问题[10],对此本文在对障碍物进行膨胀处理的基础上根据障碍物的大小、形状以及位置划分农田中的矩形区域以简化农田中复杂的工作环境,矩形分区方法具体方案为:对于膨胀处理后不是矩形或正方形的障碍物,设置纵向虚拟分割线沿x轴正方向扫描,在不规则障碍物边界的y值发生变化时留下虚拟分割线标记,通过此方法将不规则障碍物划分为多个矩形障碍物(图2a);对于2个障碍物横向或纵向边界坐标相等的情况,设置对应的横向或纵向连接线;对于矩形或正方形障碍物,过障碍物的左上角顶点与右下角顶点画垂直于x轴、y轴的分区线。
|
图 2 矩形分区(a)与矩形分区合并(b)结果 Fig. 2 The results of rectangular partition (a) and merge of partitions (b) A2、B、C、D、E、F与G表示膨胀处理后的障碍物;l1、l2、l3、l4、l5、l6、l7表示由矩形分区方案得到的横向或纵向障碍物间连接线,l8表示不规则障碍物的纵向虚拟分割线;数字1~21表示矩形分区的编号 A2, B, C, D, E, F and G represent obstacles after expansion treatment; l1、l2、l3、l4、l5、l6、l7 represent the transverse or longitudinal connection lines between obstacles obtained by the rectangular partition scheme, l8 represents the longitudinal virtual cutting line of the irregular obstacle; the numbers 1−21 represent the number of the rectangular partitioning |
对相邻分区间分区边缘线长度相等的情况进行分区的合并操作,优先合并可纵向合并的分区,之后再合并可横向合并的分区,合并结果如图2b所示。
2 优化分区间遍历顺序 2.1 旅行商问题模型农业机器人在矩形分区间以及分区内遍历完成对农田工作区域的全覆盖。为减少机器人的路径重复率,需要确定遍历各分区时的最佳遍历顺序,这本质上是一个旅行商问题(Travelling salesman problem,TSP),即将所有矩形分区归一化为由分区中心点代表的质点,在此基础上寻找一条遍历所有质点且所有质点均遍历一次的最短路径,可由数学模型进行表示。
在栅格化环境建模图中易知质点i与质点j之间的距离
| $R = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{d_{ij}} {x_{ij}}} } {\text{,}}$ | (1) |
其中,若质点i、j的连线位于最短遍历回路上则
| ${\rm{s}}{\rm{.}}\; {\rm{t}}.\; \left\{ {\begin{array}{*{20}{l}} {\displaystyle\sum\limits_{i = 1}^n {{x_{ij}} = 1} } \\ {\displaystyle\sum\limits_{j = 1}^n {{x_{ij}} = 1 } } \\ {\displaystyle\sum\limits_{i \in S} {\sum\limits_{j \in S} {{x_{ij}} \leqslant |S| - 1,\; 2 \leqslant |S| < n - 1} } } \end{array}} \right.{\text{,}}$ | (2) |
式中,S表示所有质点的非空子集,
本文通过蚁群算法求解旅行商问题。蚁群算法通过蚂蚁群体以正反馈的形式在质点间迭代遍历以寻找相对最优质点间遍历路径。蚁群算法中蚂蚁k在一段路径中遍历时会留下信息素同时该段路径中的信息素浓度也会按一定速率挥发[13],则t时刻质点i、j连线路径的信息素浓度
| ${\tau _{ij}}(t + 1) = (1 - \rho ) {\tau _{ij}}(t) + \Delta {\tau _{ij}}{\text{,}}$ | (3) |
式中,
| $\Delta {\tau _{ij}}{\rm{ = }}\sum\limits_{k = 1}^m {\Delta \tau _{ij}^k} {\text{,}}$ | (4) |
式中,
| $\Delta \tau _{ij}^k{\rm{ = }}Q/{L_k}{\text{,}}$ | (5) |
通过状态转移概率确定蚂蚁k在第t次迭代时由质点i转到质点j遍历的概率(
| $p_{ij}^k = \left\{ {\begin{array}{*{20}{l}} {\dfrac{{{{\left[ {{\tau _{ij}}\left( t \right)} \right]}^\alpha }{{\left( {{\eta _{ij}}} \right)}^\beta }}}{{\displaystyle\sum\nolimits_{k \in {\rm{allowed}}} {\tau _{ik}^\alpha \left( t \right){{\left( {{\eta _{ik}}} \right)}^{\;\beta} }} }},}&{j \in {\rm{allowe}}{{\rm{d}}_k}}\\ {0,}&{{\text{其他}}} \end{array}} \right.{\text{,}}$ | (6) |
式中,为防止蚂蚁k重复遍历质点,建立蚂蚁k遍历的禁忌表
针对蚁群算法易陷入局部最优解以及算法运行前期工作效率较慢的问题,本文分别通过人工免疫算法与粒子群算法改进遗传算法的选择与交叉算子,并将改进后的选择与交叉算子与原遗传算法变异算子与蚁群算法相结合改进传统蚁群算法信息素更新方法,具体改进方案如下:
2.3.1 选择算子蚂蚁在质点间遍历完1次之后会形成1个由质点遍历顺序代表的可行解。为提高算法的收敛速度,需通过路径代价与多样性指数构建适用度函数并通过轮盘赌选择算子对适用度值较低的可行解进行筛选。为提高可行解集的多样性、避免算法陷入局部最优解,本文通过人工免疫算法中抗体浓度[16]的概念反向定义可行解(r)的多样性指数(
| ${H_r}{\rm{ = }}\sum\limits_{p = 1}^m {\sum\limits_{q = 1}^n {h_q^{p,r}} } /m\;\;\;\;{\text{,}}$ | (7) |
| $h_q^{p,r}{\rm{ = }}\left\{ {\begin{array}{*{20}{l}} {0,}&{{\rm{if}}\;h_q^p = h_q^r}\\ {1,}&{{\rm{if}}\;h_q^p \ne h_q^r} \end{array}} \right.{\text{,}}$ | (8) |
式中,p表示可行解,
通过Euclidean距离定义可行解(r)的路径代价(
| ${L_r} = \sum\limits_{q = 1}^{n - 1} {\sqrt {{{({x_q} - {x_{q + 1}})}^2} + {{({y_q} - {y_{q + 1}})}^2}} } {\text{,}}$ | (9) |
则可行解(r)的适用度函数(
| ${f_r} = {\lambda _1} {H_r}/({\lambda _2} {L_r}){\text{,}}$ | (10) |
式中,
粒子群优化算法在处理TSP时通过各可行解向全局最优解靠拢实现群体收敛,具有较高的群体收敛速度。本文将粒子群算法的思想与遗传算法交叉算子相结合,即在蚂蚁种群迭代完一次之后,将各可行解以一定的概率与当前迭代中适用度值最大的可行解进行交叉操作,以此获得优质基因片段。具体交叉过程如图3所示。选择可行解中的2个位置,采用部分映射[17-18]的方法将2个父代解的部分结构加以替换重组而生成新可行解。

|
图 3 交叉操作 Fig. 3 Interlace operation 数字表示分区编号,间隔开的1组分区编号表示1种分区间遍历顺序 Each number represents the partitioning number, and the interval partitioning numbers in a group represents a traversal order among partitionings |
在交叉操作之后继而进行可行解的变异操作,以防止蚁群算法陷入局部最优解,如图4所示,以一定的概率变动可行解的某些基因座上的基因值完成变异操作。
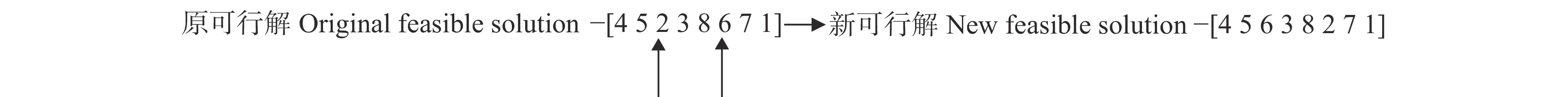
|
图 4 变异操作 Fig. 4 Mutation operation |
将选择、交叉变异后的新可行解代入公式(3)、(4)、(5)以更新各路径信息素并继续进行蚁群算法的下一次迭代。
3 分区间的衔接遍历选择下个分区4个顶点中距离上个分区遍历终点较近的顶点作为下个分区遍历的起点,而上分区终点与下分区起点可能相距较远,本文从路径代价最优的角度出发通过改进的BFS算法[19]规划分区间终点与起点的衔接路径。
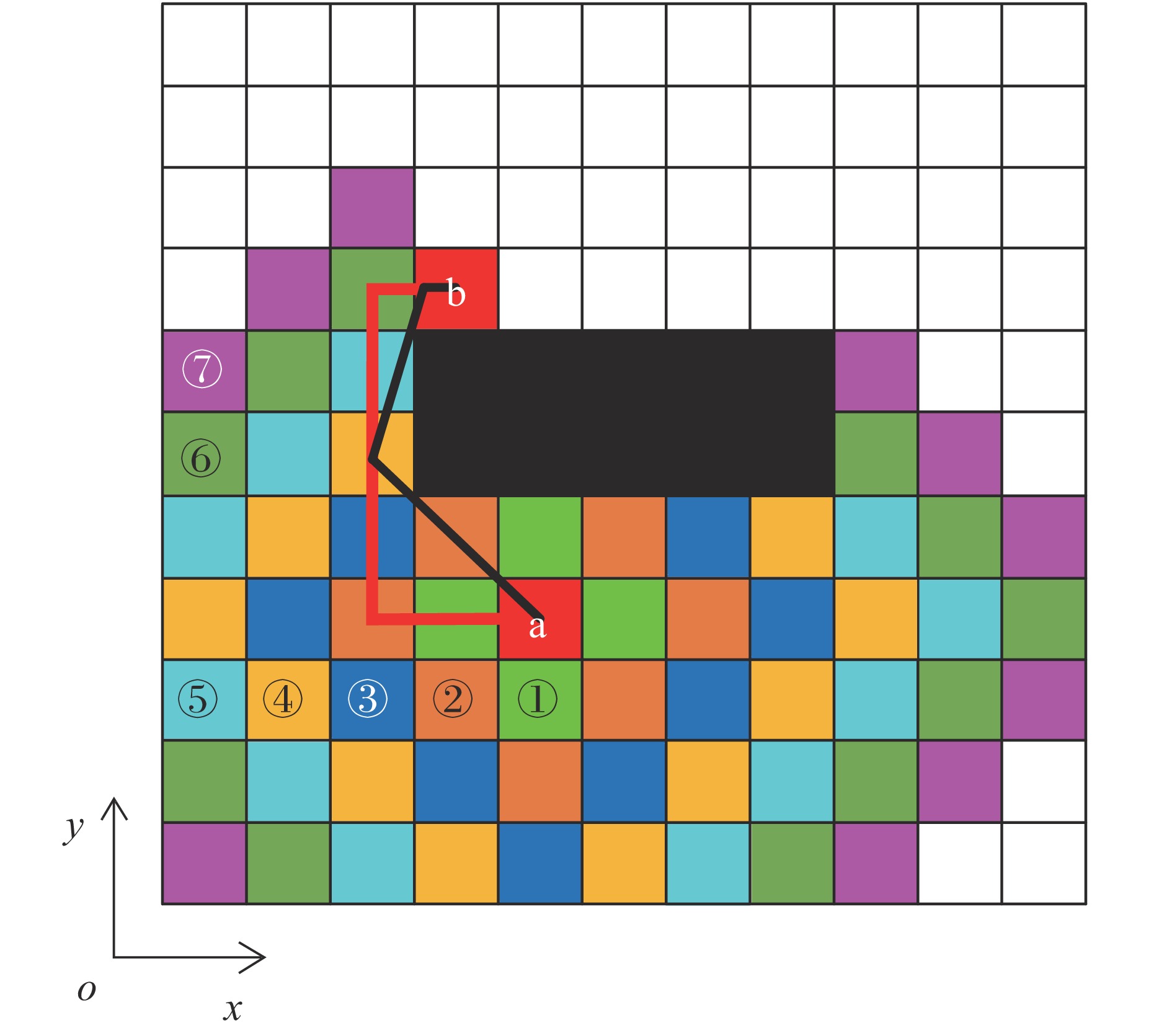
BFS算法由起点(x,y)出发,按照向上(x,y+1)、向下(x,y−1)、向左(x−1,y)、向右(x+1,y)4个方向搜索邻接点,再根据4个方向搜索邻接点的邻接点,以此类推直至到达终点。BFS算法的工作过程如图5所示。由图5可知,BFS算法找到的最短路径均由平行于坐标轴的直线组成,并未实现真正意义上的路径最优,本文根据两点之间直线最短的原则在BFS算法路径规划的基础上设计路径简化方案,即:设置一质点
|
图 5 BFS算法工作原理图 Fig. 5 Diagram of BFS algorithm working principle a、b分别为遍历的起点与终点;①~⑦代表的不同颜色的方格表示BFS算法搜索的顺序;黑色矩形表示障碍物;红色粗实线为BFS算法规划的路径,黑色粗实线为改进的BFS算法规划的路径 In this figure, a and b are the starting and ending points of the traversal respectively; The squares with different colors represented by ①−⑦ represent the search order of BFS algorithm; The black rectangle represents the obstacle; The red solid line is the path planned by BFS algorithm, the black solid line is the path planned by the improved BFS algorithm |
| ${f_e}(x) \cap {\rm{M}} \ne \emptyset {\text{。}}$ | (11) |
则记录第e次迭代的线段
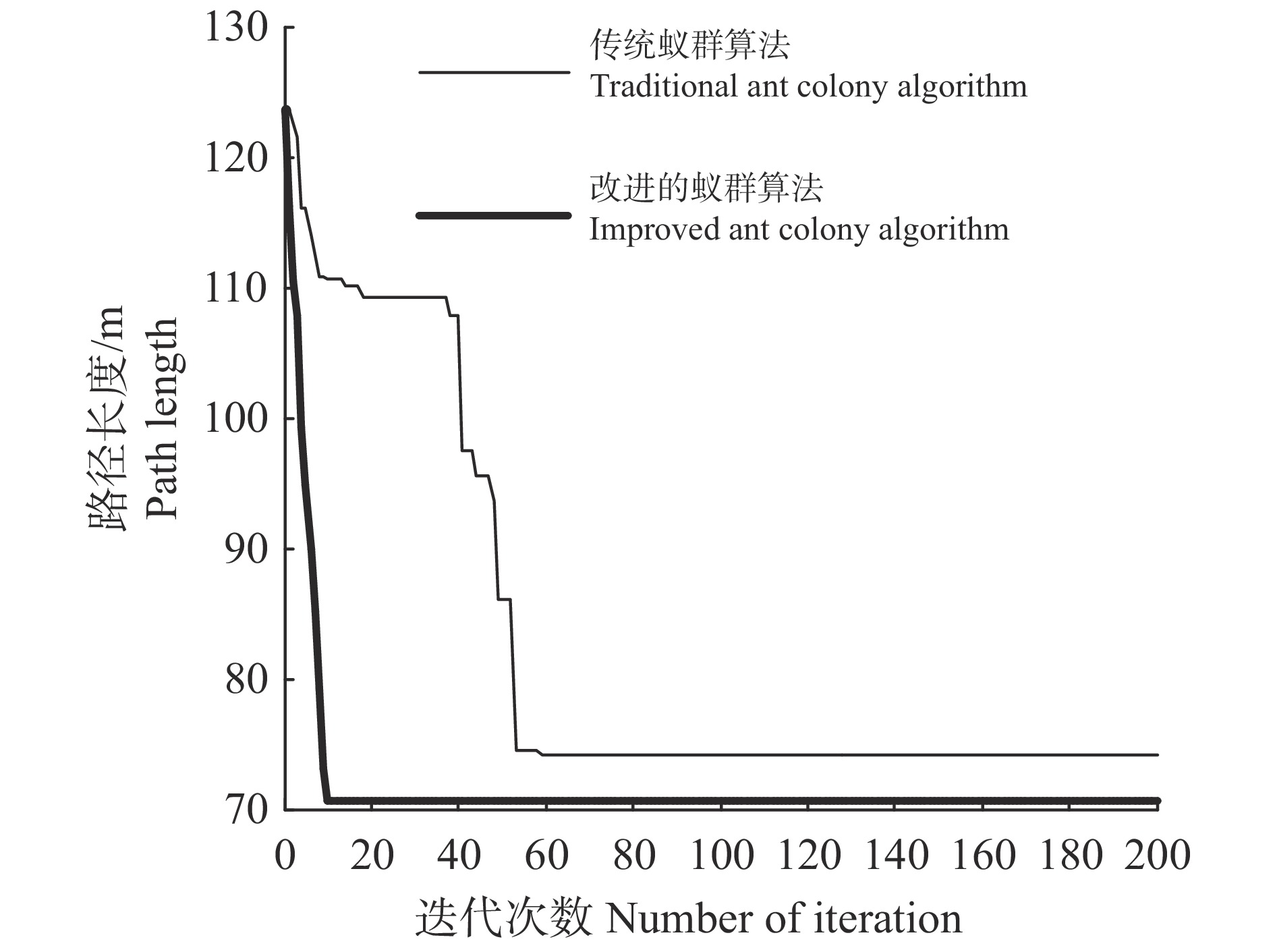
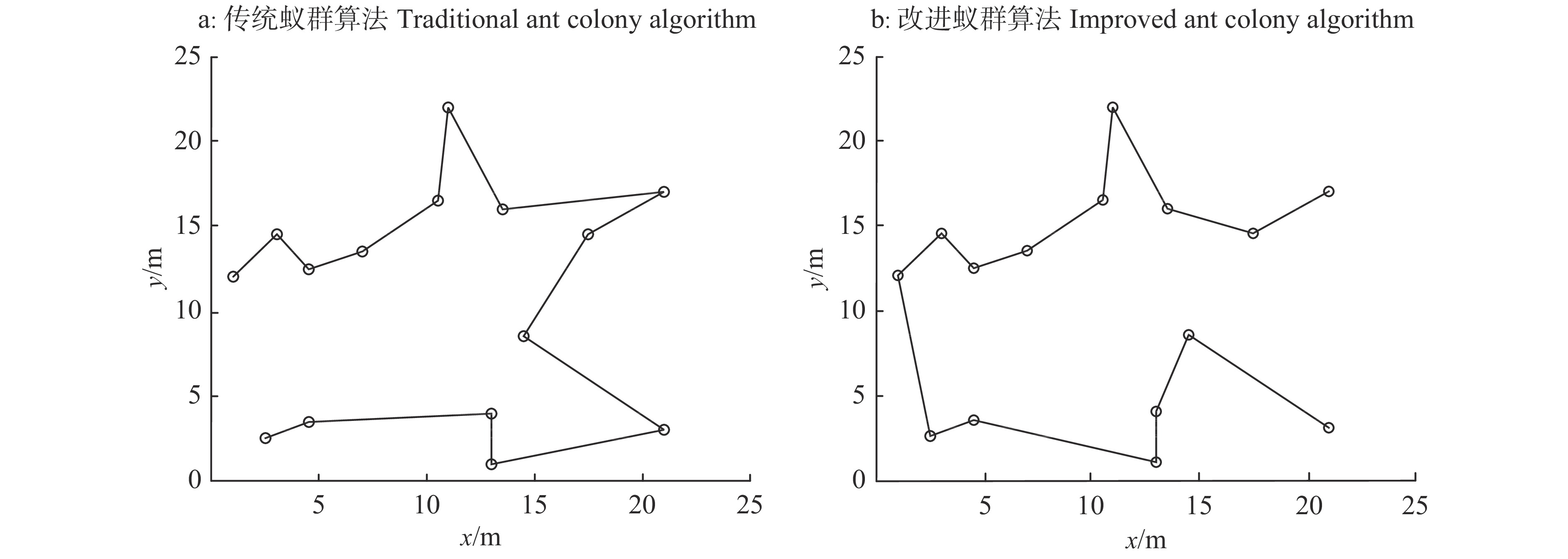
在矩形分区合并的基础上,将各分区归一化为由分区中心点代表的质点,分别由传统蚁群算法与改进蚁群算法确定各质点间的遍历顺序,以算法运行时间一致设置两算法的蚂蚁数量、信息素与启发函数权重因子、迭代次数、信息素强度Q等初始参数。2种算法历代群体最短路径随迭代次数的变化曲线如图6所示,2种算法在质点间的路径遍历图见图7。
|
图 6 2种算法最短路径长度随迭代次数的变化曲线 Fig. 6 The variation curve of the shortest path length with the number of iterations of two algorithms |
由图6可知,本文改进的蚁群算法在第10代时已收敛且最短路径长度为70.27 m,传统蚁群算法在第59代时收敛,最短路径为73.82 m。改进蚁群算法收敛时的迭代次数较传统蚁群算法减少了83.1%,路径长度相比减少4.8%。证明本文通过个体多样性定义蚁群算法适应度函数与通过遗传算法、粒子群算法与蚁群算法相结合设置信息素更新方法的方案可提高蚁群算法的收敛速度、以及蚁群算法跳出局部最优解的能力。
|
图 7 2种算法的质点间路径遍历图 Fig. 7 The graph of path traversal among particles of two algorithms |
为减少机器人的转弯次数,机器人在分区内遍历时沿矩形分区的长边作往返式遍历。通过传统蚁群算法、改进的蚁群算法与传统BFS算法、改进的BFS算法4种算法之间两两搭配出4种路径遍历方式,统计农业机器人在4种路径遍历方法下的路径重复率。
由表1可知在质点间遍历顺序一致时,由改进的BFS算法统计出的路径重复率分别是传统BFS算法的90%和80%,证明本文设置的路径简化方案有利于减少农业机器人工作时的路径重复率;在衔接路径方案一致时,质点间遍历距离越大路径重复率越高,由改进蚁群算法统计出的路径重复率分别是传统蚁群算法的70%与62%,证明优化分区间的遍历顺序可降低农业机器人在农田中遍历的路径重复率;由改进的蚁群算法与改进的BFS算法规划的机器人遍历路径重复率是传统蚁群算法与BFS算法的56%。
|
|
表 1 4种路径遍历方法下的农业机器人路径重复率 Table 1 The path repetition rate of agricultural robot under four path traversal methods |
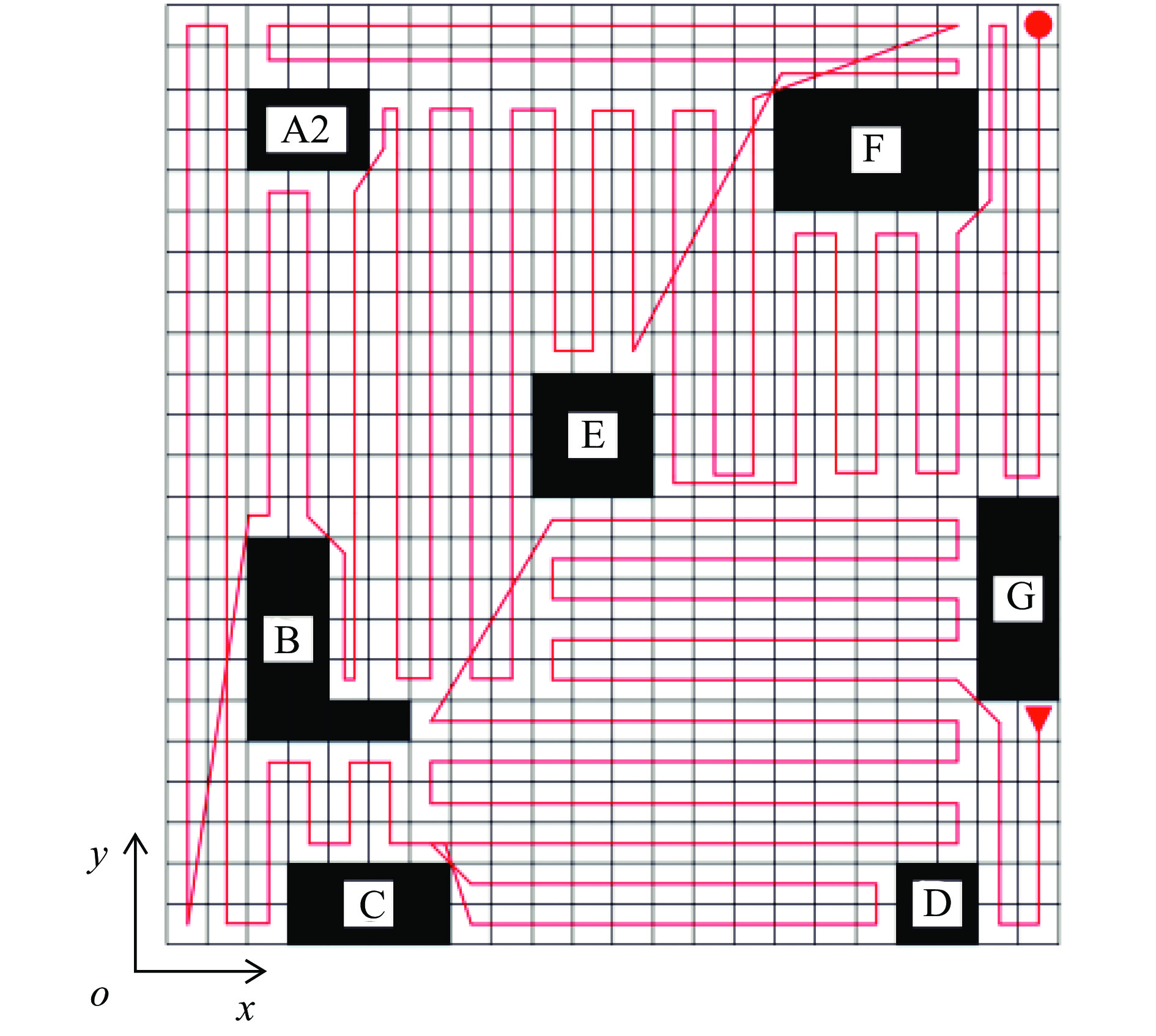
在矩形分区合并的基础上通过改进的蚁群算法与改进的BFS算法规划的遍历路线如图8所示,由图8可知,农业机器人能实现对农田工作区域100%的覆盖。
|
图 8 机器人路径遍历图 Fig. 8 Robot path traversal diagram 图中红色三角形与红色圆形分别表示整个遍历路径的起点与终点,红色线条为本文规划的遍历路径;A2、B、C、D、E、F与G表示膨胀处理后的障碍物 In this figure, the red triangle and the red circle respectively represent the starting and ending points of the entire traversal path, the red line is the traversal route planned in this paper; A2, B, C, D, E, F and G represent obstacles after expansion treatment |
针对传统蚁群算法收敛速度慢、易陷入局部最优的问题,通过建立多样性指数与引入粒子群算法的方式改进遗传算法的选择与交叉算子,并通过选择、交叉与变异操作建立改进的蚁群算法信息素更新方法。仿真结果表明,改进蚁群算法收敛时的迭代次数与算法规划的路径长度较传统蚁群算法分别减少了83.1%与4.8%。
针对农业机器人在复杂农田环境下的全区域覆盖问题,通过改进的蚁群算法解决栅格分区中分区间的遍历顺序问题,通过建立动态函数改进的BFS算法以此进行跨区域衔接路径规划。仿真结果表明,在矩形分区环境建模的基础上通过改进的蚁群算法与改进的BFS算法相结合规划的遍历路径其路径重复率为11.06%,且可实现对农田区域100%的覆盖。
| [1] |
LAN Y B, CHEN S D. Current status and trends of plant protection UAV and its spraying technology in China[J]. International Journal of Precision Agricultural Aviation, 2018, 1(1): 1-9. (  0) 0) |
| [2] |
PATHAK R, BARZIN R, BORA G C. Data-driven precision agricultural applications using field sensors and unmanned aerial vehicle (UAVs)[J]. International Journal of Precision Agricultural Aviation, 2018, 1(1): 19-23. (  0) 0) |
| [3] |
唐东林, 袁波, 胡琳, 等. 储罐探伤爬壁机器人全遍历路径规划方法[J]. 工程设计学报, 2018, 25(3): 253-261. DOI:10.3785/j.issn.1006-754X.2018.03.002 (  0) 0) |
| [4] |
李伟莉, 赵东辉. 基于栅格法与神经元的机器人全区域覆盖算法[J]. 机械设计与制造, 2017(8): 232-234. DOI:10.3969/j.issn.1001-3997.2017.08.065 (  0) 0) |
| [5] |
CHOI Y H, LEE T K, BAEK S H, et al. Online complete coverage path planning for mobile robots based on linked spiral paths using constrained inverse distance transform[C]//Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems. Missouri, USA: IEEE, 2009: 5788-5793.
(  0) 0) |
| [6] |
KAPANOGLU M, OZKAN M, YAZICI A, et al. Pattern-based genetic algorithm approach to overage path planning for mobile robots[M]. Berlin: Springer Berlin Heidelberg, 2009.
(  0) 0) |
| [7] |
李楷, 陈永府, 金志勇, 等. 基于回溯法的全覆盖路径规划算法[J]. 计算机工程与科学, 2019, 41(7): 1227-1235. DOI:10.3969/j.issn.1007-130X.2019.07.012 (  0) 0) |
| [8] |
曹翔, 俞阿龙. 移动机器人全覆盖信度函数路径规划算法[J]. 智能系统学报, 2018, 13(2): 314-321. (  0) 0) |
| [9] |
聂杨. 智能割草机器人的关键技术研究[D]. 重庆: 重庆大学, 2018.
(  0) 0) |
| [10] |
张堂凯. 己知环境下智能清洁机器人路径规划研究[D]. 南京: 南京邮电大学, 2017.
(  0) 0) |
| [11] |
谭阳. 求解广义旅行商问题的若干进化算法研究[D]. 广州: 华南理工大学, 2013.
(  0) 0) |
| [12] |
马慧茹, 赵峰, 贾利民, 等. 基于随机机会约束规划模型的旅行商问题及其求解算法[J]. 长安大学学报(自然科学版), 2015, 35(S1): 179-183. (  0) 0) |
| [13] |
陈志, 韩兴国. 改进蚁群算法在移动机器人路径规划上的应用[J]. 计算机工程与设计, 2020, 41(8): 2388-2395. (  0) 0) |
| [14] |
周兰凤, 杨丽娜, 方华. 基于蚁群算法的滑移预测路径规划研究[J]. 华东师范大学学报(自然科学版), 2020(4): 72-78. (  0) 0) |
| [15] |
王槐彬, 彭雪, 周诗源, 等. 机器人导航路径的动态分级蚁群算法规划策略[J]. 机械设计与制造, 2020(6): 95-99. DOI:10.3969/j.issn.1001-3997.2020.06.024 (  0) 0) |
| [16] |
YANG D D, JIAO L C, NIU R C, et al. Investigation of combinational clustering indices in artificial immune multi-objective clustering[J]. Computational Intelligence, 2014, 30(1): 115-144. DOI:10.1111/j.1467-8640.2012.00466.x (  0) 0) |
| [17] |
SAHIN O, AKAY B. Comparisons of metaheuristic algorithms and fitness functions on software test data generation[J]. Applied Soft Computing, 2016, 49: 1202-1214. DOI:10.1016/j.asoc.2016.09.045 (  0) 0) |
| [18] |
TIAN T, GONG D W. Test data generation for path coverage of message-passing parallel programs based on coevolutionary genetic algorithms[J]. Automated Software Engineering, 2016, 23(3): 469-500. DOI:10.1007/s10515-014-0173-z (  0) 0) |
| [19] |
彭紫微. 面向多种体系结构的BFS算法研究[D]. 长沙: 国防科技大学, 2018.
(  0) 0) |
 2021, Vol. 42
2021, Vol. 42


