智慧化无人农业是将传感数据与智能决策作为管控全局的要素^[1]，并结合多传感信息融合技术、人机交互技术与云边协同计算技术对农业机器人进行信息化管理的现代农业^[2]。解决农业机器人在智慧化无人农场中的全区域覆盖问题可减少机器人工作区域的重复率，达到对农田工作区域的全覆盖，是当下急需解决的关键问题。

针对机器人全区域覆盖的环境不同，全区域覆盖问题可分为静态已知环境的覆盖与动态未知环境的覆盖^[3-4]。农业机器人所面对的大田作业一般为静态已知环境下的离线预规划地图覆盖问题，目前已有的研究多通过栅格法与单元分解法简化机器人全区域覆盖的复杂工作环境^[5]。通过对复杂工作环境进行栅格化处理，完成全区域覆盖，可保证机器人遍历的精度，如贺利乐等^[6]通过机器人本体上的传感器构建基于动态栅格法的工作环境，从而保证机器人实现路径全覆盖，但系统开展机器人全区域覆盖的计算量会随区域地图的增大而呈指数式增加^[7-8]；单元分解法则根据工作区域中现有障碍物的形状、大小、位置与区域分解规则将整体工作区域划分成多个虚拟子区域，以完成对复杂工作区域的简化^[9]，如胡诗宇^[10]利用栅格法对环境地图建模，通过矩形分解的思想对地图单元分解，并通过深度优先搜索算法求解子区域之间的遍历顺序，但深度优先搜索算法只适用于求解可行解，不能找到区域间最优遍历顺序。

本文通过栅格法与单元分解法相结合，简化农业机器人的复杂工作环境；通过改进的模拟退火算法，求解机器人在分区间的最优遍历顺序；通过A*算法与八邻域搜索法相结合的方法，进行机器人的跨区域衔接路径规划，以此完成农业机器人对工作区域的全区域覆盖。

1 栅格化农田与矩形分区

本文从山东理工大学兰玉彬团队与淄博禾丰种业科技股份有限公司共建的智慧化无人农场的实际农业生产环境出发，定义农业机器人的复杂工作环境，即智慧化无人农场中存在的由纵横交错的田间道路自然分割的离散分布的数片农田，以及农田中存在的一些分散障碍物如农田中的风力发电机、电线杆、固定安装的传感器等构成了农业机器人复杂的工作环境^[11]。

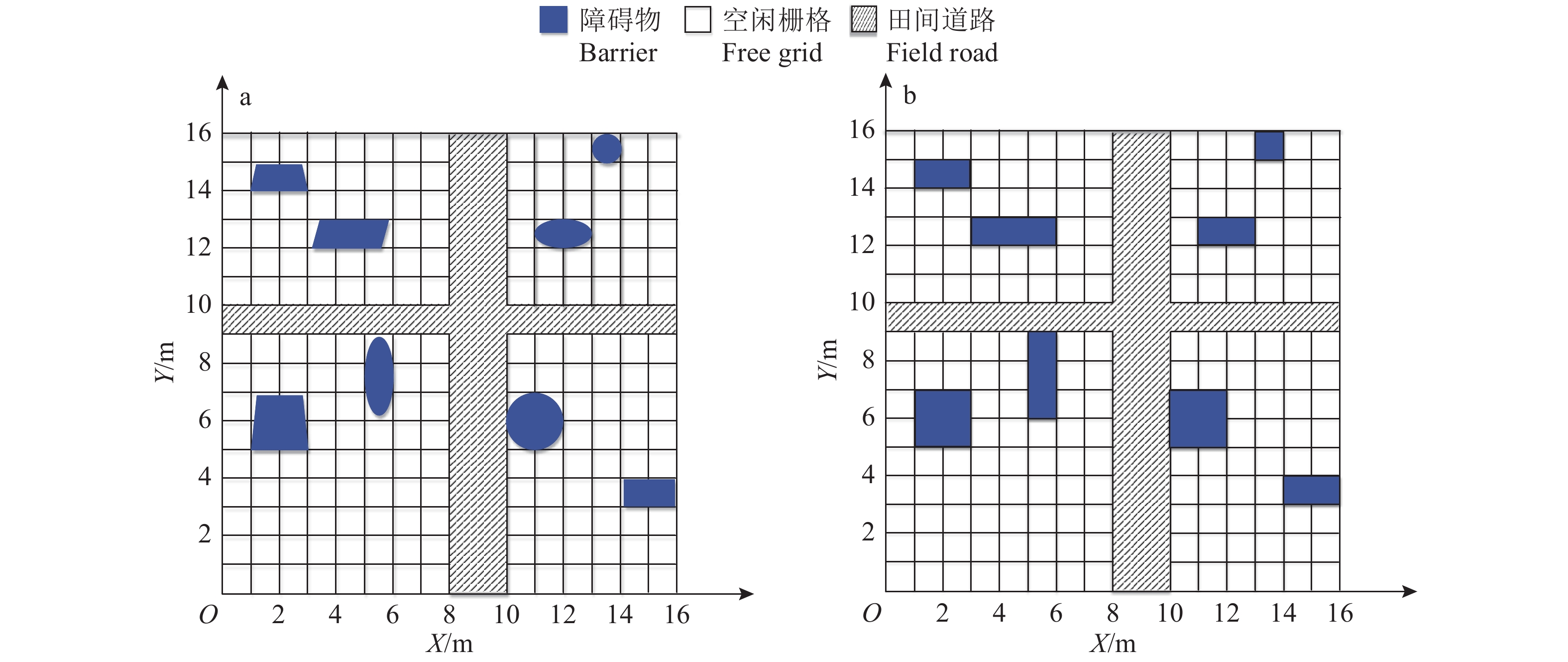
1.1 栅格化农田与障碍物膨胀处理

根据本文建立的复杂农田工作环境概念，定义工作环境地图并参考文献[12]方法对此区域进行栅格化处理，将农业机器人的工作范围设置为栅格图的单位长度。农田环境与农田栅格化结果如图1a所示。为避免农业机器人在全遍历过程中陷入死角，本文针对边界与栅格线不重合的障碍物进行二值化膨胀处理^[13]，处理后的效果如图1b所示。

1.2 栅格分区与分区合并

为简化农业机器人进行大田作业时的复杂工作环境，本文将由田间道路自然分割形成的单片农田作为一级工作区域分区，并在一级工作区域分区内根据农田区域中障碍物的形状、大小与位置划分农业机器人可自由遍历的二级工作区域分区，通过农业机器人在一级分区与二级分区内的遍历完成对农田工作区域的全区域覆盖。

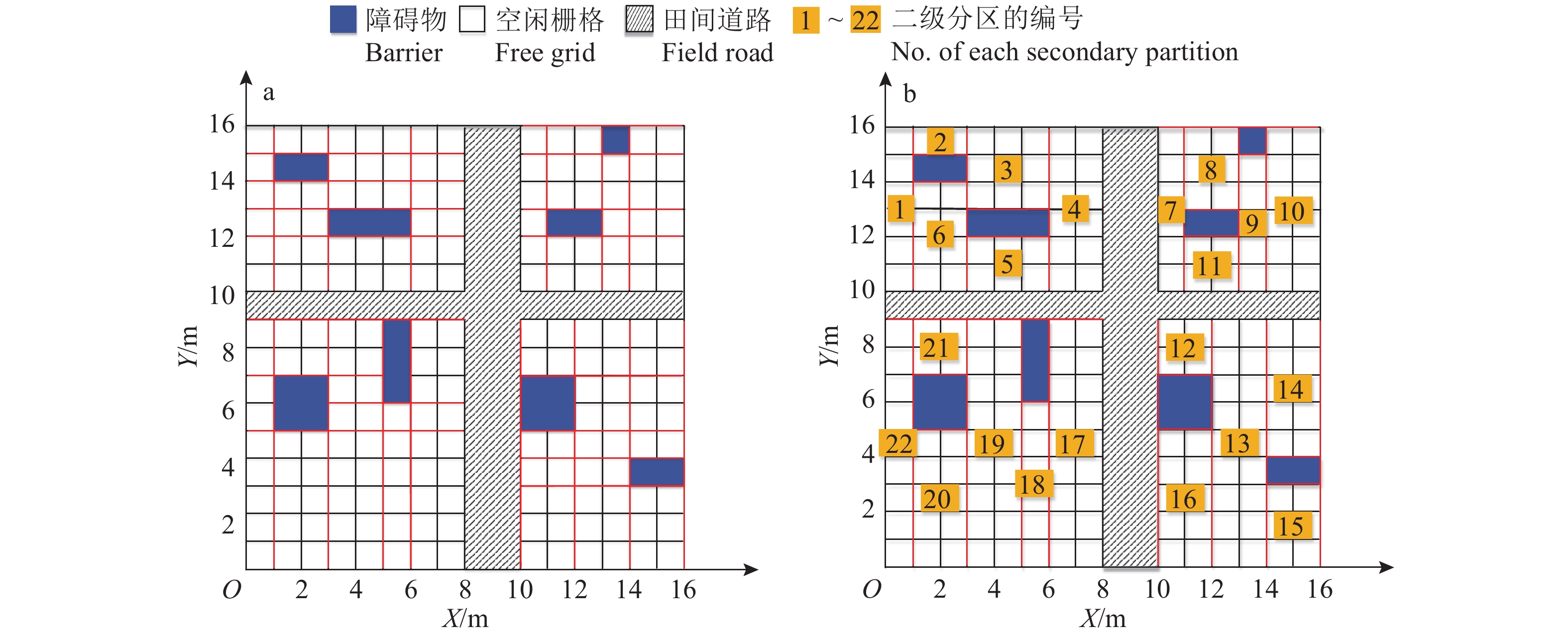
划分二级栅格分区具体方案为：分别过障碍物膨胀处理后的左下角顶点与右上角顶点作垂直于X轴的分区线，遇到其他障碍物或田间道路即停止；分别过障碍物膨胀处理后的左上角顶点与右下角顶点作垂直于Y轴的分区线，遇到其他障碍物或田间道路即停止。在图1b的基础上进行栅格分区的结果如图2a所示。

工作区域中二级分区的数量与机器人遍历面积重复率成正比，为减少机器人的路径重复率，本文在栅格分区的基础上进行分区合并操作。一个栅格分区与其邻近分区共同边长度相等则可以进行分区合并^[14]，分区时先合并可纵向合并的分区，再合并可横向合并的分区。分区合并结果如图2b所示。

2 基于模拟退火算法求解旅行商问题

优化农业机器人在分区间的遍历顺序可减少农业机器人在分区间的衔接路径，进而减少其遍历路径重复率、提高工作效率。本文在优化各一级分区遍历顺序之后再优化各一级分区内二级分区的遍历顺序，通过农业机器人在一级分区与二级分区内的遍历，实现整体工作区域的全覆盖。寻找农业机器人在分区间的最佳遍历顺序本质上是一个旅行商问题^[15]。

2.1 旅行商问题

将图2b中的各分区抽象化为一个个由分区重心点代表的质点，则旅行商问题可以描述为：旅行商从某个质点出发访问，寻找一条遍历全部r个质点且每个质点仅遍历1次的最短路径^[16]，即搜索自然子集N={1，2，…，r}中各元素(质点编号)的排序，使得遍历各质点的路径长度(R)最小：

$ R={\displaystyle \sum\nolimits _{j=1}^{r-1}d({V}_{{\eta }_{j}}, \;{V}_{{\eta }_{j+1}})}, $

(1)

式中， $ {\eta _j} $ 为排序之后自然子集N中的第j位数字。 $ d({V}_{{\eta }_{j}}, {V}_{{\eta }_{j+1}}) $ 表示N中第j位的质点到第j+1位的质点的距离^[17]。所得最短质点间遍历顺序即为最佳分区间遍历顺序。

2.2 模拟退火算法

模拟退火算法因其随机跳变接受新解的特性而具有较好的收敛速度与寻优能力^[18]，故本文通过模拟退火算法求解旅行商问题。算法求解旅行商问题时首先设定初始温度、降温速率与链长等参数，并建立模拟退火算法所得可行解i的适应度值 $ {f_i} $ 为：

$ {f_i}{\text{ = }}1/{R_i}{{,}} $

(2)

式中， $ {R_i} $ 表示可行解i的路径长度。

算法在不断降温的过程中通过多种变换法生成新解，并根据Metropolis准则以概率的形式选择是否保留此解，则算法温度为T时新解i被接受的概率P为：

$ P = \left\{ {\begin{array}{*{20}{l}}{ 1, }&{{f_i} > {f_{i - 1}} }\\ { \exp \Bigg( - \dfrac{{{f_i} - {f_{i - 1}}}}{T}\Bigg), }&{{f_i} \leqslant {f_{i - 1}} }\end{array}} \right. $

(3)

式中， $ {f_{i - 1}} $ 表示新解i前的旧解i−1的适应度值，算法达到所设定的温度终止阈值时则停止迭代，同时，输出所得最优解。由公式(3)可知，在新解的适应度值大于旧解适应度值时，算法以100%的概率接受新解i，反之，以概率P接受新解i，算法当前运行温度与概率P成正比，新解i的适应度值与概率P成反比。

3 基于自适应升温的模拟退火算法

本文提出基于贪婪机制的优质可行解生成方法与基于自适应升温的模拟退火算法改进方法，以提高模拟退火算法求解旅行商问题的寻优能力与收敛性能。

3.1 基于贪婪机制的优质可行解生成方法

传统模拟退火算法通常采用2变换法与3变换法生成新解，本文在以上2种方法的基础上借鉴遗传算法变异操作的思想，提出关于模拟退火算法的第3种新解生成方法即遗传变异法。模拟退火算法新解生成方法如图3所示。

2变换法任意选择2个原解中的位置，将2个位置中间的排列顺序进行倒置操作以生成新解，将此种方法得到的新解适应度值记为swap2(f)；3变换法任意选择3个位置，将前两个位置间的数字置于第3个数字后以生成新解，将此种方法得到的新解适应度值记为swap3(f)；遗传变异法通过交换随机选择的2个数字的位置以生成新解，将此种方法得到的新解适应度值记为swap4(f)。

本文计算以上3种方法生成的新解的适应度值，并借鉴贪婪机制逐步寻找局部最优以达到全局最优的思想，只保留适应度值高的新解对应的状态[ $ {\text{State swap}}(f) $ ]作为算法的实时新状态(New state)，即：

$ \begin{split} &\quad\quad\quad\quad\quad\quad\quad{\text{New state }} =\\ &{\rm{ State}}\min \{ {\text{swap}}2(f),{\text{swap}}3(f),{\text{swap}}4(f){\text{\} }}。\end{split} $

(4)

3.2 基于自适应升温的模拟退火算法

在模拟退火算法陷入局部最优解时，人为提高算法运行的温度，有助于提高算法对于较差解的接受概率，进而有更大的可能跳出局部最优解。若算法运行中产生的可行解的邻域内无比该解更优的可行解，即：

$ \max {\text{\{ }}{f_{k - L/100}}{\text{, }}\cdots {\text{ , }}{f_{k - 1}}{\text{, }}{f_{k + 1}}{\text{, }}\cdots {\text{ , }}{f_{k + L/100}}{\text{\} }} \leqslant {f_k}{{,}} $

(5)

则将其定义为算法已陷入局部最优，式中k表示算法陷入局部时在当前温度下已迭代的次数，L表示算法链长。

进行局部升温操作时若升温幅度过小，则较差解的接受概率提升效果有限，达不到跳出局部最优解的效果；若升温幅度过大，则算法对较差解的接受概率接近100%^[19]，算法寻优又会进入漫长的全局搜索，严重降低算法的收敛速度。故本文建立解集多样性的概念以设计自适应升温策略。算法运行过程中产生的各可行解组成一个解集，根据算法所记录的解集实时最优适应度值 $ {f_{\max }} $ 与解集实时平均适应度值 $ {f_{{\text{avg}}}} $ 的关系定义当前解集多样性 $ {F_\beta } $ ：

$ {F_\beta } = \frac{{{f_{\max }} - {f_{{\text{avg}}}}}}{{{f_{\max }}}}{{,}} $

(6)

当 $ {f_{{\text{avg}}}} $ 的值逐渐接近 $ {f_{\max }} $ 时，表明此时解集多样性减小。种群多样性越低，算法陷入局部最优的可能性越大，升温幅度应越大。

此外，本文根据局部最优解与 $ {f_{\max }} $ 之间的适应度值大小关系，将该局部最优解分为3个等级，局部最优解的适用度值越接近 $ {f_{\max }} $ ，算法升温幅度越小，由此，自适应升高的温度 $ \Delta T $ 为：

$ \begin{split} &\quad\quad\quad\quad\quad\quad\quad\quad\quad\Delta T =\\ & \left\{ {\begin{array}{*{20}{l}}{ \Delta {T_{\min }}, }&{{\text{ 0}}{\text{.9}}{f_{\max }} < {f_k} \leqslant {f_{\max }} }\\ { \Delta {T_{\max }} - \dfrac{{{f_k}}}{{{f_{\max }}}} (\Delta {T_{\max }} - \Delta {T_{\min }}), }&{{\text{ 0}}{\text{.4}}{f_{\max }} < {f_k} \leqslant 0.9{f_{\max }} }\\ {\Delta {T_{\max }}, }&{ {f_k} \leqslant 0.4{f_{\max }} }\end{array}} \right. \end{split} $

(7)

$ \Delta {T_{\max }} = \left\{ {\begin{array}{*{20}{l}} {0.8T,\;\;{\text{ 0 < }}{F_\beta } \leqslant {\text{0}}{\text{.3}}} \\ {0.7T,\;\;{\text{ 0}}{\text{.3 < }}{F_\beta } \leqslant {\text{0}}{\text{.7}}} \\ {0.6T,\;\;{\text{ 0}}{\text{.7 < }}{F_\beta }{\text{ < 1}}} \end{array}} \right. $

(8)

式中，T为算法当前温度， $ \Delta {T_{\min }} $ =0.3T。

4 基于A*算法的分区间衔接路径

农业机器人在一个分区内完成遍历工作时，需根据改进模拟退火算法规划的分区间最优遍历顺序转至下个分区起点继续遍历。由于农业机器人工作环境的复杂性，上个分区终点与下个分区起点可能并不连续，所以，为了提高农业机器人的工作效率，降低农业机器人的遍历路径重复率，本文以路径重复率为优化目标，通过A*算法规划机器人分区间的衔接路径。

A*算法通过建立从起始点到目标点的评价函数规划两点间的最优路径，评价函数 $ e(m,n) $ 计算式为：

$ e(m,n) = g(m,n) + h(m,n), $

(9)

式中， $ g(m,n) $ 表示从起始点( $ {x_{{\text{start}}}} $ , $ {y_{{\text{start}}}} $ )到当前点(m,n)的实际代价函数， $ h(m,n) $ 表示从当前点到目标点( ${x_{{\text{goal}}}}$ , ${y_{{\text{goal}}}}$ )的启发代价函数。实际代价函数由Euclidean距离之和组成，当前点(m,n)与上一个已确定路径的栅格( $ {m_0} $ , $ {n_0} $ )之间的Euclidean距离 $ Q(m,n) $ 为：

$ Q(m,n){\text{ = }}\sqrt {{{(m - {m_0})}^2} + {{(n - {n_0})}^2}} {{,}} $

(10)

$ g(m,n){\text{ = }}\sum\nolimits_{t = 1}^v {{Q_t}} + Q(m,n){{,}} $

(11)

式中， $\displaystyle\sum\nolimits_{t = 1}^v {{Q_t}}$ 表示前t( $ t \in [1,v] $ )次迭代搜索的路径中相邻栅格之间的Euclidean距离之和。

启发代价函数表示一种预估距离，此函数的存在能够保证机器人始终向目标点移动^[20]，本文中启发代价函数 $ h(m,n) $ 通过曼哈顿距离实现：

$ h(m,n) = |m - {x_{{\text{goal}}}}| + |n - {y_{{\text{goal}}}}| 。$

(12)

通过八邻域搜索法搜索当前点(m,n)的周围栅格，即(m−1,n+1)、(m,n+1)、(m+1,n+1)、(m+1,n)、(m+1,n−1)、(m,n−1)、(m−1,n−1)、(m−1,n)。将以上栅格作为当前点代入评价函数计算其路径代价，在路径代价最小的栅格基础上继续使用A*算法与八邻域搜索法重复以上过程探索路径直至目标点。

5 算法仿真与试验验证

为验证改进模拟退火算法的收敛能力与寻优能力，以及农业机器人全区域覆盖策略对路径重复率的优化效果。本文分别通过Matlab 2014软件对改进模拟退火算法与农业机器人全区域覆盖策略进行仿真分析。

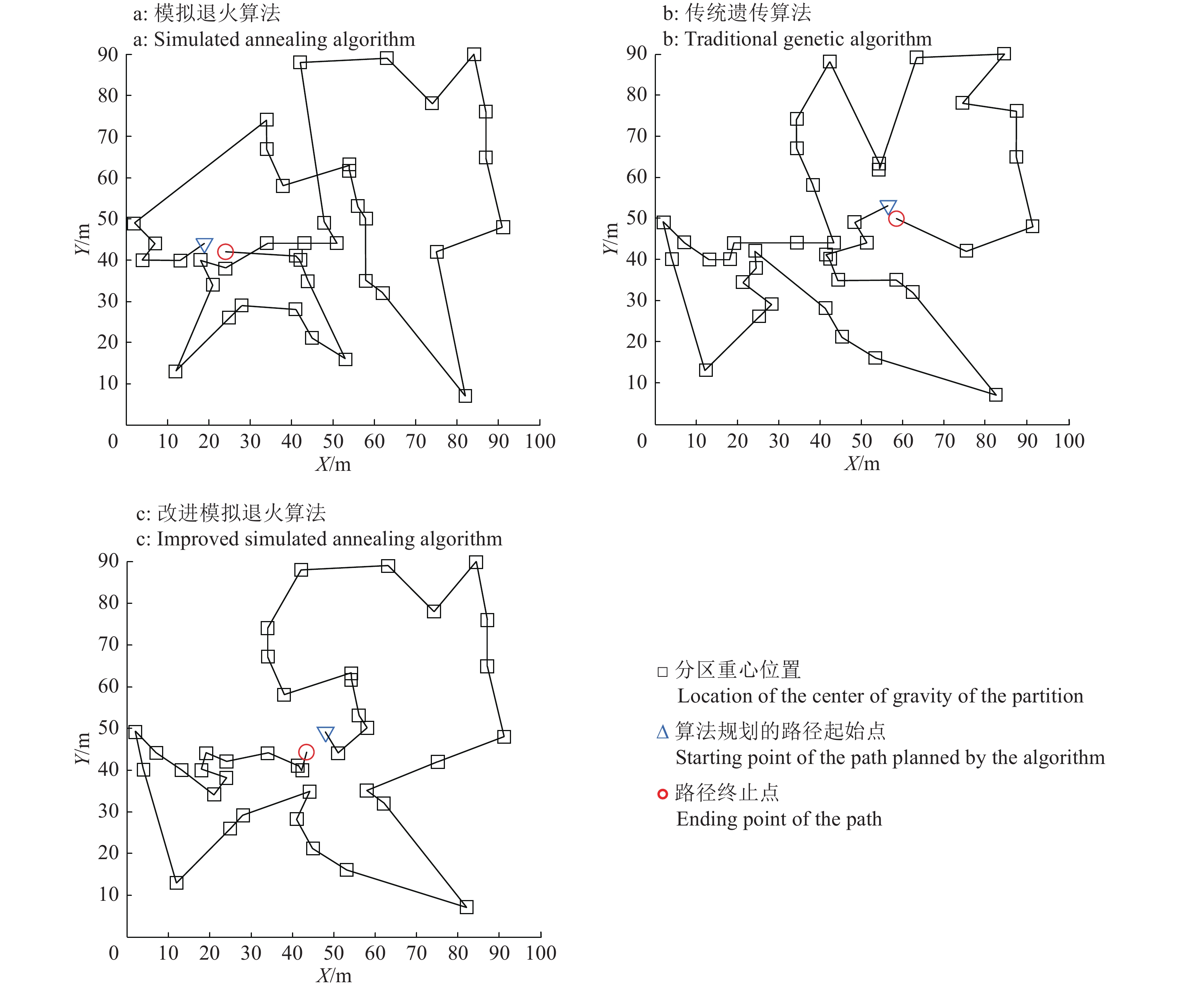
5.1 改进模拟退火算法仿真

定义3组分别包含20、30、40个分区的重心点坐标，对比传统遗传算法、模拟退火算法与本文改进模拟退火算法规划各组最优路径所得到的路径长度、算法收敛时的迭代次数，结果如表1所示。3个算法规划40个分区的最优遍历路径如图4所示。

由表1可知，在分区数量为20、30时，3种算法均能得到相近的路径长度，但在分区数量为20时，改进模拟退火算法收敛时的迭代次数较模拟退火算法和传统遗传算法分别减少了63.3%和66.7%；在分区数量为30时，改进模拟退火算法收敛时的迭代次数较模拟退火算法和传统遗传算法分别减少了35.5%和72.0%。由表1和图4可知，在分区数量为40时，改进的模拟退火算法所获得的路径长度分别比模拟退火算法和传统遗传算法减少了14.7%和10.1%，收敛时的迭代次数分别减少了9.8%和59.1%。

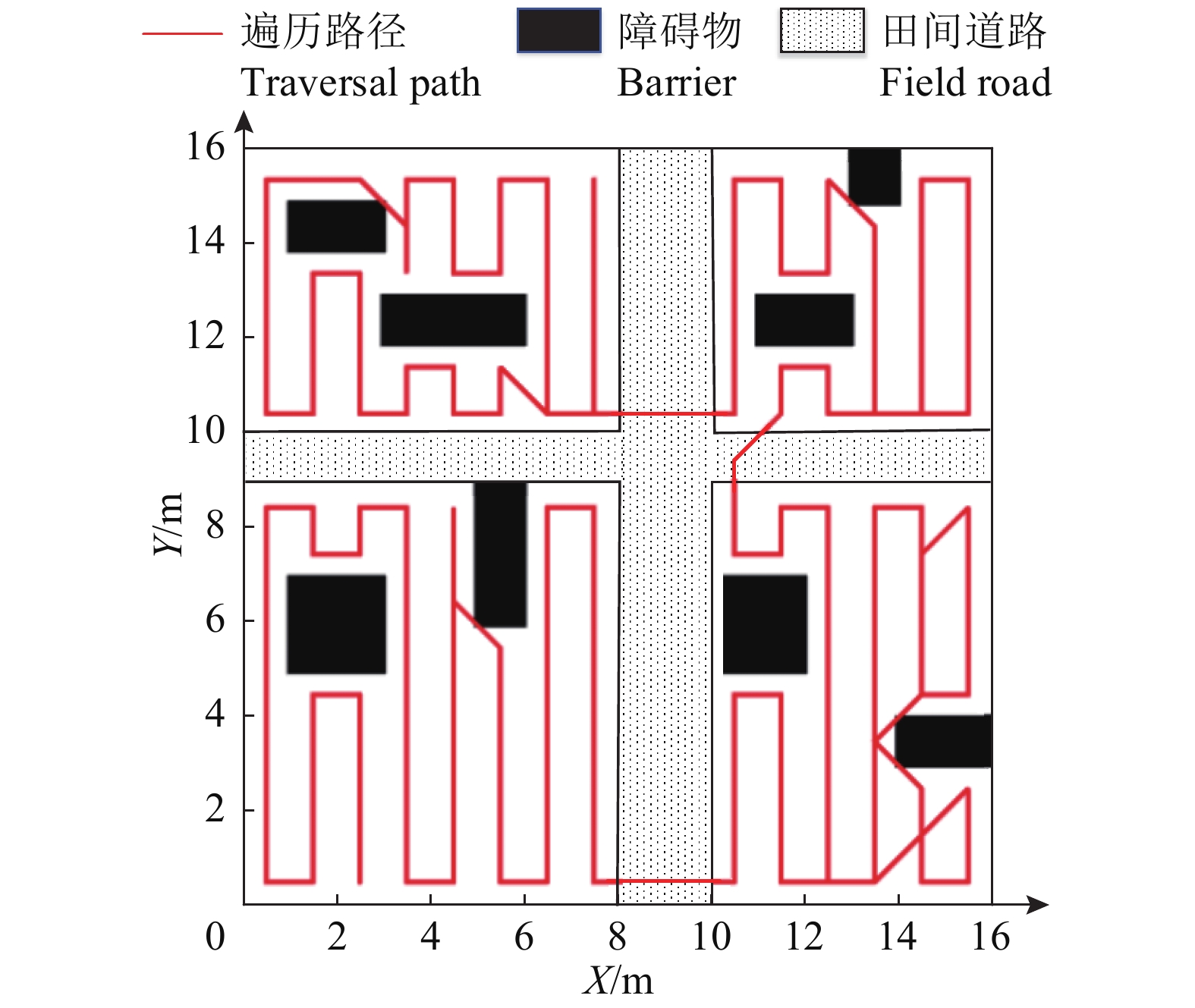
5.2 路径遍历仿真

为减少机器人的转弯次数，机器人在分区内遍历时沿矩形分区的长边作往返式遍历。选择下个分区中最靠近上个分区终点的单元格作为下个分区的起点。农业机器人在图2b基础上进行的路径遍历仿真如图5所示。

图2b中农业机器人可自由遍历的工作面积为189 m²，图5中机器人移动总面积为222 m²，机器人遍历路径重复率为14.86%，工作区域覆盖率接近100%。

5.3 试验验证

为验证本文全区域覆盖策略对农业机器人遍历面积重复率与覆盖率的优化作用，以山东理工大学兰玉彬团队研发的高地隙喷药机器人为对象进行全区域覆盖遍历试验。

通过智慧化无人农场云平台人机交互界面将整体工作区域划分为由虚拟道路分割成的4个子区域，在整体工作区域中设置分散的11个异形障碍物，并以此为环境地图进行机器人路径规划。

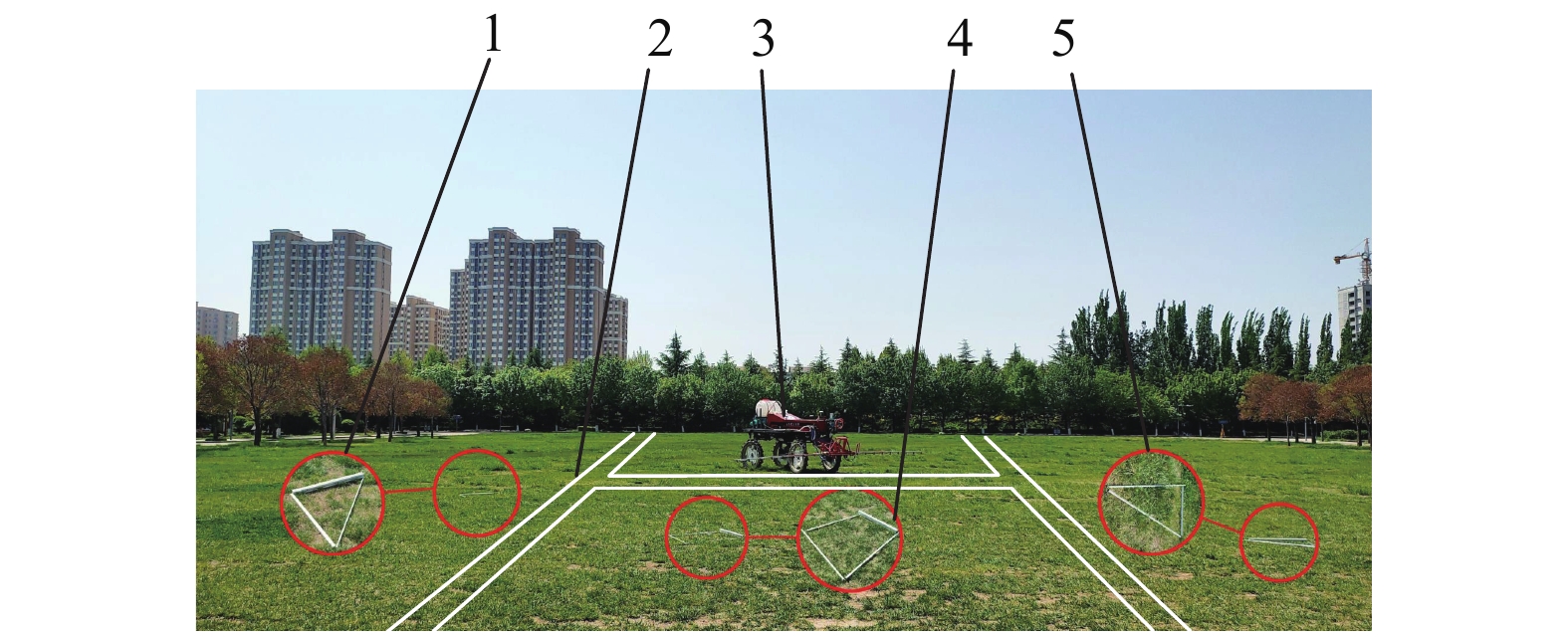
本试验中高地隙喷药机器人双臂喷药杆展开后的工作范围为10 m，行驶速度为1.7 m/s，试验工作区域面积为0.8 hm²。高地隙喷药机器人、部分异形障碍物放大图与虚拟道路分割线如图6所示。

根据高地隙喷药机器人遍历过程中实时回传至农场云平台的工作数据可知，高地隙喷药机器人使用9.1 min完成整体工作区域的遍历，实际遍历面积为0.927 hm²，遍历面积重复率为15.83%，工作区域覆盖率接近100%。

6 结论

本文引入遗传算法变异操作的思想，建立基于贪婪机制的模拟退火算法优质可行解生成方法；设定模拟退火算法陷入局部最优解的判断依据并建立算法解集多样性的概念，设计基于自适应升温的模拟退火算法改进方案，以提高算法的寻优能力与收敛速度。仿真试验表明，在分区规模为40时，改进的模拟退火算法所获得的路径长度分别比模拟退火算法和传统遗传算法减少了14.7%和10.1%，收敛时的迭代次数分别减少了9.8%和59.1%。

本文根据农场实际工作环境建立一级分区的概念，在栅格化环境建模与障碍物膨胀处理的基础上，在一级分区内部建立二级分区的栅格分区和分区合并规则。通过改进的模拟退火算法优化机器人在分区间的遍历顺序，通过A*算法与八邻域搜索法相结合进行机器人跨区域衔接路径规划。仿真试验表明，机器人遍历路径重复率为14.86%。机器人现场遍历试验表明，高地隙喷药机器人遍历面积重复率为15.83%，工作区域覆盖率接近100%。