甘蔗是我国重要的糖料作物,2019年,我国糖料蔗种植面积约153.33万hm2,位居世界第三[1]。目前甘蔗机械化收获技术存在含杂率高、损失大的突出问题,难以得到糖厂和农户的认可,严重制约了我国甘蔗收获机的推广[2-3]。甘蔗在收获过程中,物料间、物料与设备间的相互作用十分复杂,采用离散元法研究颗粒间的相互作用及运动规律,有利于揭示颗粒间相互作用机理,进而改善甘蔗输送、除杂等关键环节的作业效率,对提高甘蔗收获机性能具有重要意义。颗粒仿真参数的标定,有利于提高离散元仿真模型的精度,从而提高离散元法在颗粒间相互作用机理及运动规律研究中的准确度[4-5]。
离散元法是研究物料运动的有效工具,近年来,在农业工程研究中呈现出良好的应用前景[6]。刘凡一等[7]以小麦颗粒物理休止角为响应值,基于响应面优化标定了小麦离散元仿真参数。侯占丰等[8]通过物理试验的方法测定了冰草种子的基本物性参数和接触参数,以物理休止角为最优目标值,对离散元仿真参数进行寻优,获得最佳参数组合。吴孟宸等[9]对花生种子颗粒堆积过程进行仿真,利用堆积角试验对种间摩擦因数及种子与材料间滚动摩擦因数进行离散元仿真标定,通过台架试验验证花生模型及其仿真参数的可靠性。武涛等[10]采用颗粒间黏结力的“Hertz-Mindlin with JKR”接触模型,进行土壤堆积角仿真试验,确定了样品土壤的离散元接触参数与接触模型参数。王黎明等[11]测定了不同含水率下猪粪的堆积角,通过物理堆积试验与仿真方法对猪粪接触参数进行了标定。刘文政等[12]利用物理试验与仿真试验相结合的方法对微型马铃薯的离散元仿真参数进行了优化和标定。国内外学者还对水稻[13-14]、大豆[15]、玉米[16-17]等常见谷物以及葡萄[18]、苹果[19-20]等水果进行了参数标定。综上所述,目前农业物料离散元仿真模型参数标定主要集中在粮油种子、土壤、肥料以及生物质颗粒等球形/类球形微小颗粒,以及水果等类球形大颗粒。堆积角试验是进行离散元仿真参数标定的主要方法,对于上述颗粒,对堆积角影响显著性较大的参数主要为恢复系数、静摩擦系数、滚动摩擦系数。切段式甘蔗收获机的收获物为甘蔗段,与上述传统球形/类球形物料不同,蔗段属于大长径比秆状物料,对这类物料堆积角影响较显著的仿真参数尚不清楚,影响了离散元法在蔗段运动学分析和CFD-EDM耦合除杂机理研究方面的应用。因此,亟需进行蔗段离散元建模方法和参数标定研究。
本文以蔗段为研究对象,选用多球聚合模型和XML的方法构建蔗段仿真模型,根据国内外研究确定蔗段仿真参数范围,以物理试验获取的蔗段堆积角为响应值,通过Plackett-Burman试验、最陡爬坡试验和Box-Behnken试验对离散元仿真参数进行标定,得到最优参数组合,最终通过物理试验与仿真试验的对比验证,确定离散元仿真参数的可靠性。以期为蔗段等大长径比非球形物料离散元仿真参数标定提供参考。
1 蔗段基本物性参数与堆积角测定 1.1 蔗段基本物性参数测定选取广东雷州半岛南光6队农场种植的‘桂糖49’甘蔗为研究对象,采用华南农业大学自主研制的HN4GDL-194型切段式甘蔗联合收获机为收获设备,对切段后的甘蔗进行基本物性参数(几何尺寸、密度、含水率)测量。
随机选取30根蔗段作为样本,测量基本物理参数,取其平均值。采用卷尺、电子游标卡尺(0.02 mm)、电子秤(0.01 g)测量蔗段几何尺寸和质量,采用排水法测量体积,采用电热干燥法测量含水率。试验测得蔗段几何尺寸(长×直径)的均值为283.08 mm×32.06 mm,标准差分别为2.23和1.60,蔗段的平均质量为192 g,密度为1.19 g/cm3,含水率(w)为73.15%。
1.2 蔗段物理堆积角测定堆积角是表征散装物料流动、摩擦等性质的宏观参数,与物料种类、长径比、形状和含水率等因素有关,因此堆积角试验常被用作散装物料的离散元标定[10]。蔗段物理堆积角的测量方法为:采用华南农业大学自主研制的甘蔗田间运输车,将蔗段从田间运输车的输送臂卸到公路运输车内,蔗段从相对高度1500 mm处落下,待所有蔗段静止后,在公路运输车内形成稳定的甘蔗堆,用角度测量仪测量蔗段堆积角,试验重复10次,获得蔗段物理试验堆积角为39.40°~45.80°,平均值为42.70°,标准差为2.6。蔗段物理堆积试验,如图1所示。

|
图 1 蔗段物理堆积试验 Fig. 1 Physical repose angle test of sugarcane segment |
球形颗粒形状简单、规则,只有1个尺寸参数,因此在离散元仿真软件中,一般选用球形颗粒建立物料的仿真模型。考虑到离散元仿真效率,通常球形/类球形物料离散元模型可以用单个球形颗粒进行简化[21]。但实际中,大多数物料都是不规则的,无法通过单一球形进行简化建模,为使离散元仿真模型更符合实际物料特性,需采用非球形颗粒模型的构建方法。
非球形颗粒建模通常采用多球聚合模型(Multi-sphere method,MSM)[22-24]和多球黏结模型(Bonded particle method,BPM)[25-26]。多球聚合模型(图2a)由多个颗粒堆叠聚合而成,该离散元模型与实际物料轮廓相对吻合,且在EDEM软件中被视为一个独立体。多球黏结模型(图2b)由多个直径相同的颗粒通过“黏结键”粘连而成,颗粒间相互独立,半径越小,越接近实际物料轮廓,但是会增加仿真时间,适用于DEM-CFD耦合仿真[13,27]。
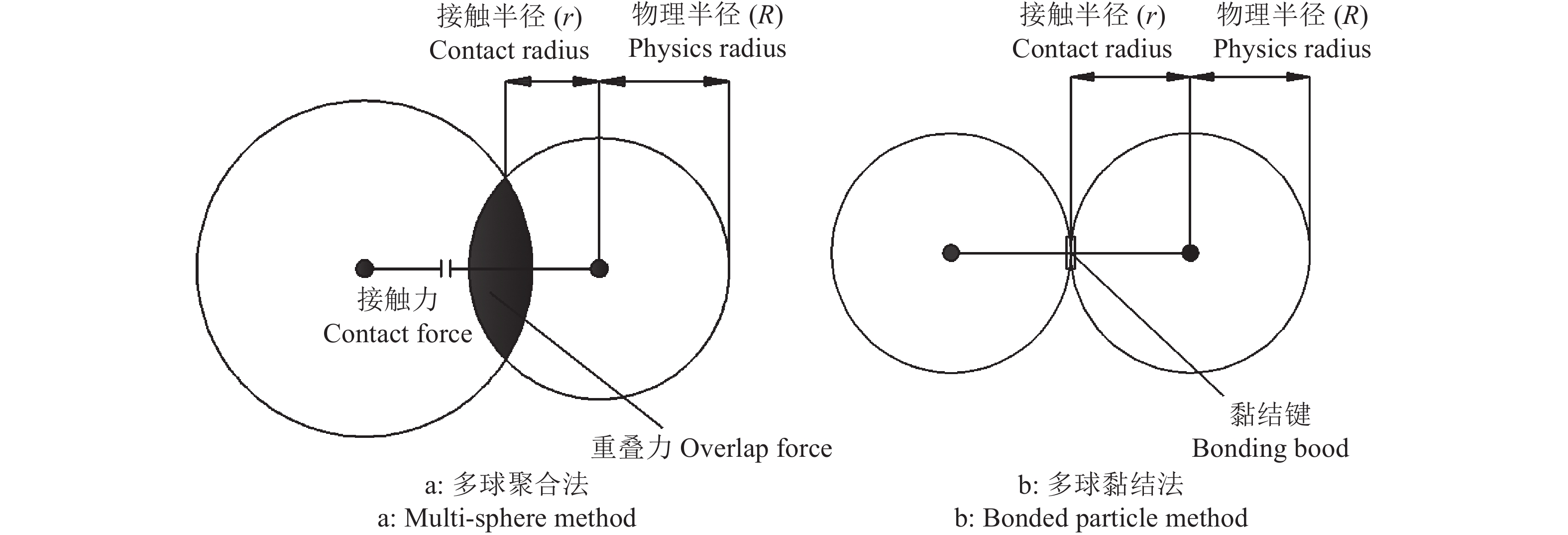
|
图 2 非球形颗粒建模方法 Fig. 2 Modeling method of non-spherical particles |
非球形颗粒模型填充方法有手动填充、API颗粒替换和XML等方法。手动填充常用于少量球形颗粒填充的简单模型。API颗粒替换和XML方法常用于大量球形颗粒填充建模,可提高构建颗粒模型的速度和精度。API颗粒替换方法需要调用相应插件完成小颗粒替换大颗粒并建立黏结键的过程,小颗粒之间相互独立,常用于磨损、破裂方面的研究[28]。XML方法是在EDEM后处理模块导出.xml 格式文件中,调整数据文件中颗粒的坐标得到目标颗粒,所有颗粒被视为一个整体[29],常用于不考虑磨损、破裂等问题的模型构建。
2.2 蔗段模型构建蔗段属于秆状物料模型,在简化此类物料模型结构时,不考虑物料的外观细微变化[30]。根据前期物理试验得到的蔗段基本物理参数,采用Solidworks建立几何模型,将蔗段模型保存为.stl格式导入EDEM中。本文选用多球聚合模型和XML的方法构建蔗段仿真模型,定义颗粒工厂在蔗段内部上端,动态生成的颗粒自由下落至模型内部,颗粒间采用Hertz-Mindin无滑移接触模型。利用154个半径为8 mm的颗粒自动填充蔗段模型,填充完成后,导出所有球形颗粒的中心坐标.csv格式文件,对文件中的数据进行处理。将仿真时间归零,导出格式为.xml的DEC文件,将EDEM中新建的paricle项目导入.xml格式文件后,软件自动生成的蔗段离散元仿真模型,可作为颗粒模板,进行后续仿真调用,蔗段的离散元模型如图3所示。

|
图 3 蔗段的仿真模型 Fig. 3 Simulation model of sugarcane segment |
根据蔗段的物理堆积角试验,简化仿真试验几何模型。物理试验时,输送臂只起到将蔗段提升至一定高度的作用,蔗段从输送带上输送、抛散、下落,散开后竖直下落的最大圆周直径约400 mm,竖直下落的初始位置与输送臂末端高度差约300 mm,与运输车箱底板高度差约1500 mm,蔗段下落到运输车内,稳定后蔗段堆的最大散落直径约1500 mm。仿真时,为了提高效率,简化去掉输送臂和运输车,将蔗段竖直下落的初始位置设置为漏斗下开口,竖直下落的初始位置正上方300 mm处设置为颗粒工厂(漏斗上开口),公路运输车简化为单一接料板。
在EDEM中建立漏斗(上、下开口直径分别为500 mm和400 mm、高度300 mm、下端面离地高度为1500 mm)和接料板(直径1500 mm),设置颗粒工厂在漏斗上方口径处,总生成量为1400根,生成速率为100根/s,仿真时间为16 s,仿真蔗段的堆积过程,如图4所示。

|
图 4 堆积角仿真模型 Fig. 4 Repose angle of simulation model |
蔗段仿真堆积角图像处理过程,如图5所示。
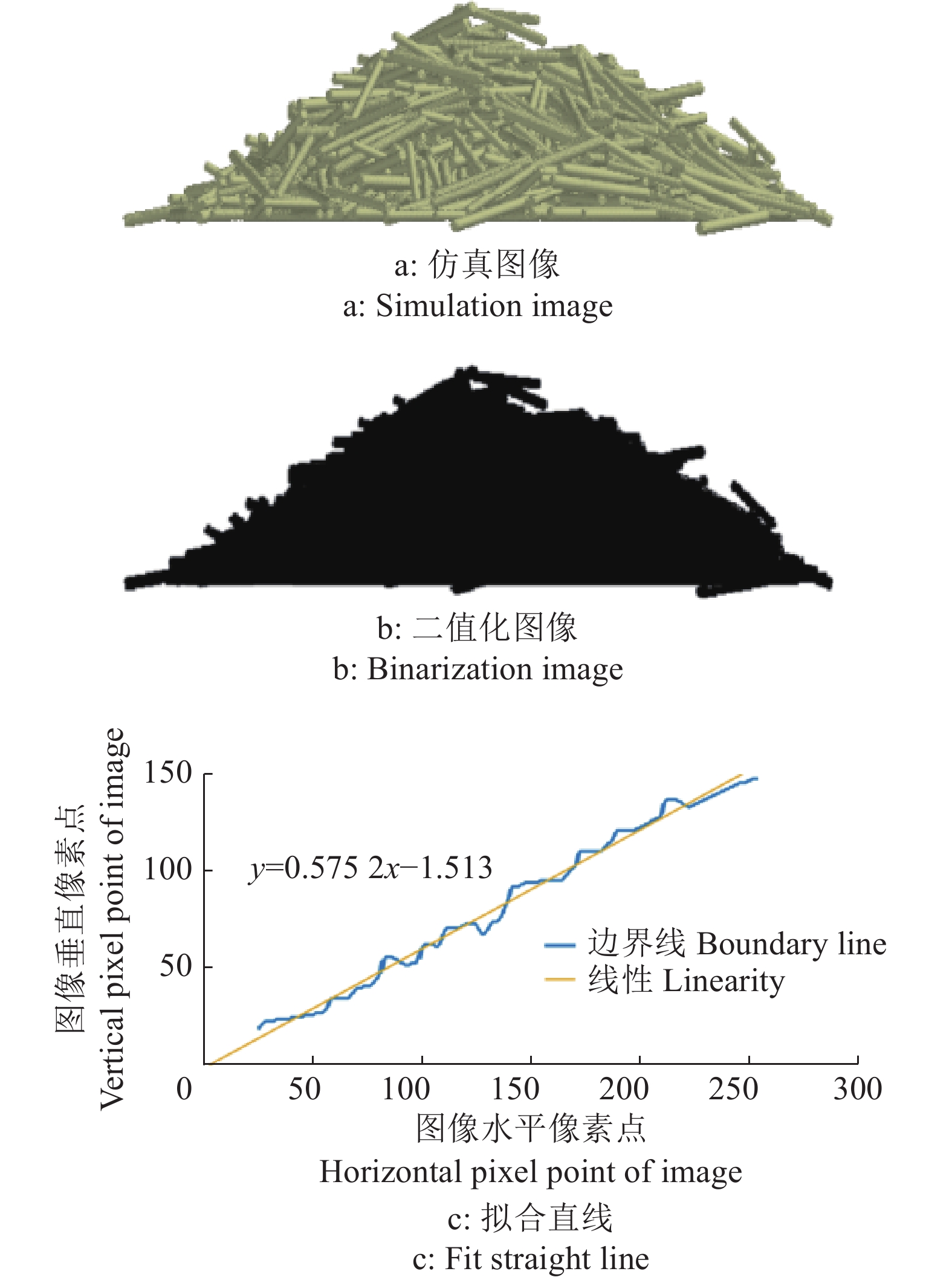
|
图 5 图像处理 Fig. 5 Image processing |
仿真试验中,为了更准确地测量仿真堆积角,采用计算机图像处理技术对其进行处理。首先在EDEM中截取仿真蔗段堆的正视图,如图5a所示,再利用Matlab软件对获得的图像进行灰度化、二值化(图5b)、边界像素点的搜索与提取,最后通过线性拟合获取拟合方程,得到方程斜率K[31]。蔗段堆积角(θ)计算公式[32]为:
| $ \theta = \frac{{\tan \left| K \right| \times 180}}{\text{π} } \text{,} $ | (1) |
式中:K为拟合曲线方程的斜率。
由于蔗段堆X、Y方向两侧倾角存在一定差异,因此测量视图两侧的倾角,取其平均值为仿真堆积角,如图6所示。

|
图 6 蔗段离散元仿真模型堆 Fig. 6 DEM simulation model stack of sugarcane segment |
仿真试验时,需要用到蔗段和钢板的基本物性参数和表面接触参数,通过查阅文献[33-39]对蔗段与钢板力学特性的测定及离散元仿真中仿真参数的设置,确定本研究中各仿真参数的取值范围:蔗段的泊松比为0.30~0.38、剪切模量为3.0~18.6 MPa、密度为1.19 g/cm3;钢板的泊松比为0.30、剪切模量为7.9×104 MPa、密度为7.85 g/cm3;蔗段−蔗段的恢复系数、静摩擦系数和滚动摩擦系数范围分别为0.30~0.60、0.30~0.80和0.01~0.06;蔗段−钢板的恢复系数、静摩擦系数和滚动摩擦系数范围分别为0.20~0.70、0.10~0.60和0~0.50。
3.2 Plackett-Burman(PB)试验为了筛选出对蔗段堆积角存在显著性影响的仿真参数,开展PB试验。利用Design-Expert.11软件对PB试验进行设计,以蔗段物理试验堆积角为响应值,进行显著性参数筛选。选取表1中的8个仿真参数的最大值、最小值作为高、低2个水平,分别编码为水平1、−1,如表1所示。以中间水平0为中心点,进行13组试验。
|
|
表 1 Plackett-Burman试验参数列表 Table 1 List of Plackett-Burman test parameters |
PB试验方案及结果如表2所示,利用Design-Expert.11软件对试验结果进行方差分析,得到各仿真参数显著性结果如表3所示。由表3可知,蔗段−蔗段静摩擦系数(X4)和蔗段−蔗段滚动摩擦系数(X5)对仿真堆积角的影响极显著(P<0.01);蔗段泊松比(X1)对仿真堆积角的影响显著(P<0.05);蔗段剪切模量、蔗段−蔗段恢复系数、蔗段−钢恢复系数、静摩擦系数、滚动摩擦系数对仿真堆积角的影响不显著。因此后续试验设计中只考虑3个影响显著的因素,对仿真堆积角影响不显著的参数取PB试验的中间水平。
|
|
表 2 Plackett-Burman试验方案及结果1) Table 2 Plackett-Burman test scheme and results |
|
|
表 3 Plackett-Burman试验参数显著性分析 Table 3 Analysis of significance of parameters in Plackett-Burman test |
为快速确定各仿真参数最优值所在区域范围,对PB试验筛选出的3个显著性参数进行爬坡试验,包括蔗段的泊松比、蔗段−蔗段的静摩擦系数、蔗段−蔗段的滚动摩擦系数。试验以仿真堆积角与物理堆积角的相对误差作为评价指标,相对误差最小的组可确定为各仿真参数最优值区域间的中心点。最陡爬坡试验方案设计及结果(表4)表明,随着3个显著性参数数值的增加,仿真堆积角与物理试验堆积角的相对误差先减小后增大,在4号水平时,相对误差最小为0.62%,可以确定最优值区域在4号水平附近,因此取4号作为中心点,3号、5号分别作为低、高水平进行后续响应面设计。
|
|
表 4 最陡爬坡试验方案设计及结果 Table 4 Design scheme and results of the steepest ascent search test |
根据最陡爬坡试验结果,以表4中4号作为中心点(0),3号和5号分别为低水平(−1)和高水平(1)进行显著性参数Box-Behnken试验,设计方案及结果如表5所示。
|
|
表 5 Box-Behnken试验设计方案及结果1) Table 5 Box-Behnken test design scheme and results |
利用Design-Expert.11件对BB试验结果进行二次多项式回归拟合,得到蔗段仿真堆积角(θ)与3个显著性参数的回归方程:
| $ \begin{split} \theta =& 42.73 - 1.34{X_1} + 1.52{X_4} + 0.5387{X_5} - \hfill \\& 0.1950{X_1}{X_4} + 0.135{X_1}{X_5} - 0.007{X_4}{X_5} - \hfill \\& 0.1529X_1^2 - 1.23X_4^2 + 1.85X_5^2。\hfill \\ \end{split} $ | (2) |
该回归模型方差分析结果如表6所示,由表6分析可知,蔗段泊松比(X1)、蔗段−蔗段静摩擦系数(X4)、蔗段−蔗段滚动摩擦系数二次项(
|
|
表 6 Box-Behnken试验回归模型方差分析 Table 6 Analysis of variance of the Box-Behnken test regression model |
利用Design-Expert.11软件的优化模块,以物理堆积角42.70°为目标值,对回归方程进行优化求解,得到多组最佳参数。从多组最佳参数组合中选取1组与物理堆积角平均值最接近的参数组合。最终选取的最佳优化组合为:蔗段泊松比0.35、蔗段−蔗段静摩擦系数0.53、蔗段−蔗段滚动摩擦系数0.04,其余非显著性参数取中间水平。
为了验证蔗段离散元标定参数的准确性,采用上述最优参数组合进行蔗段堆积角仿真试验,重复3次仿真模拟,得到的蔗段仿真堆积角分别为42.69°、43.06°和43.65°。对仿真结果与物理试验值进行独立样本t检测,得到P=0.196>0.05,表明标定后的仿真堆积角与物理试验堆积角无显著性差异,仿真试验均值(43.13°)与物理试验均值(42.70°)相对误差为0.99%,进一步验证了蔗段离散元标定参数的可靠性。蔗段堆积角仿真试验验证如图7所示。

|
图 7 堆积角仿真试验验证 Fig. 7 Verification of repose angle by simulation test |
研究通过物理试验和参考国内外文献,确定了蔗段基本参数及取值范围;并通过Plackett-Burman试验,对仿真参数进行显著性筛选。结果表明:蔗段泊松比、蔗段−蔗段静摩擦系数和蔗段−蔗段滚动摩擦系数对蔗段堆积角影响显著。与以往研究[13-20]相比较,发现泊松比对大长径比秆状物料堆积角的影响比球类、类球形物料更为显著。
通过Box-Behnken试验,以物理试验堆积角42.70°为最佳目标值,得到最优参数组合为:蔗段泊松比0.35、蔗段−蔗段静摩擦系数0.53、蔗段−蔗段滚动摩擦系数0.04。
通过独立样本t检验,对最优参数组合进行验证。结果表明仿真堆积角与物理试验堆积角无显著性差异,两者相对误差为0.99%,进一步验证了蔗段离散元标定参数的可靠性。
| [1] |
樊秋菊, 黄清玲, 吴合槟, 等. 国内外甘蔗收获机械化发展概况与前景[J]. 甘蔗糖业, 2020, 49(6): 1-11. DOI:10.3969/j.issn.1005-9695.2020.06.001 (  0) 0) |
| [2] |
刘庆庭, 刘晓雪, 武涛, 等. 我国甘蔗机械化“十四五”规划与甘蔗产业可持续发展[J]. 现代农业装备, 2020, 41(6): 2-9. DOI:10.3969/j.issn.1673-2154.2020.06.001 (  0) 0) |
| [3] |
邢浩男, 马少春, 王风磊, 等. 切段式甘蔗收割机排杂风机结构优化与试验[J]. 农业工程学报, 2020, 36(20): 67-75. DOI:10.11975/j.issn.1002-6819.2020.20.009 (  0) 0) |
| [4] |
HORABIK J, MOLENDA M. Parameters and contact models for DEM simulations of agricultural granular materials: A review[J]. Biosystems Engineering, 2016, 147(7): 206-225. (  0) 0) |
| [5] |
OINONEN A, MARQUIS G. A constitutive model for interface problems with frictional contact and cohesion[J]. European Journal of Mechanics - A/Solids, 2015, 49(1): 205-213. (  0) 0) |
| [6] |
曾智伟, 马旭, 曹秀龙, 等. 离散元法在农业工程研究中的应用现状和展望[J]. 农业机械学报, 2021, 52(4): 1-20. DOI:10.6041/j.issn.1000-1298.2021.04.001 (  0) 0) |
| [7] |
刘凡一, 张舰, 李博, 等. 基于堆积试验的小麦离散元参数分析及标定[J]. 农业工程学报, 2016, 32(12): 247-253. DOI:10.11975/j.issn.1002-6819.2016.12.035 (  0) 0) |
| [8] |
侯占峰, 戴念祖, 陈智, 等. 冰草种子物性参数测定与离散元仿真参数标定[J]. 农业工程学报, 2020, 36(24): 46-54. DOI:10.11975/j.issn.1002-6819.2020.24.006 (  0) 0) |
| [9] |
吴孟宸, 丛锦玲, 闫琴, 等. 花生种子颗粒离散元仿真参数标定与试验[J]. 农业工程学报, 2020, 36(23): 30-38. DOI:10.11975/j.issn.1002-6819.2020.23.004 (  0) 0) |
| [10] |
武涛, 黄伟凤, 陈学深, 等. 考虑颗粒间黏结力的黏性土壤离散元模型参数标定[J]. 华南农业大学学报, 2017, 38(3): 93-98. DOI:10.7671/j.issn.1001-411X.2017.03.015 (  0) 0) |
| [11] |
王黎明, 范盛远, 程红胜, 等. 基于EDEM的猪粪接触参数标定[J]. 农业工程学报, 2020, 36(15): 95-102. DOI:10.11975/j.issn.1002-6819.2020.15.012 (  0) 0) |
| [12] |
刘文政, 何进, 李洪文, 等. 基于离散元的微型马铃薯仿真参数标定[J]. 农业机械学报, 2018, 49(5): 125-135. DOI:10.6041/j.issn.1000-1298.2018.05.014 (  0) 0) |
| [13] |
张荣芳, 焦伟, 周纪磊, 等. 不同填充颗粒半径水稻种子离散元模型参数标定[J]. 农业机械学报, 2020, 51(S1): 227-235. DOI:10.6041/j.issn.1000-1298.2020.S1.026 (  0) 0) |
| [14] |
鹿芳媛, 马旭, 谭穗妍, 等. 水稻芽种离散元主要接触参数仿真标定与试验[J]. 农业机械学报, 2018, 49(2): 93-99. DOI:10.6041/j.issn.1000-1298.2018.02.012 (  0) 0) |
| [15] |
张涛, 刘飞, 赵满全, 等. 大豆种子与排种器接触物理参数的测定与离散元仿真标定[J]. 中国农业大学学报, 2017, 22(9): 86-92. DOI:10.11841/j.issn.1007-4333.2017.09.11 (  0) 0) |
| [16] |
王云霞, 梁志杰, 张东兴, 等. 基于离散元的玉米种子颗粒模型种间接触参数标定[J]. 农业工程学报, 2016, 32(22): 36-42. DOI:10.11975/j.issn.1002-6819.2016.22.005 (  0) 0) |
| [17] |
王美美, 王万章, 杨立权, 等. 基于响应面法的玉米籽粒离散元参数标定[J]. 华南农业大学学报, 2018, 39(3): 111-117. DOI:10.7671/j.issn.1001-411X.2018.03.017 (  0) 0) |
| [18] |
马帅, 徐丽明, 袁全春, 等. 葡萄藤防寒土与清土部件相互作用的离散元仿真参数标定[J]. 农业工程学报, 2020, 36(1): 40-49. DOI:10.11975/j.issn.1002-6819.2020.01.005 (  0) 0) |
| [19] |
VAN ZEEBROECK M, TIJSKENS E, DINTWA E, et al. The discrete element method (DEM) to simulate fruit impact damage during transport and handling: Model building and validation of DEM to predict bruise damage of apples[J]. Postharvest Biology and Technology, 2006, 41(1): 85-91. DOI:10.1016/j.postharvbio.2006.02.007 (  0) 0) |
| [20] |
SCHEFFLER O C, COETZEE C J, OPARA U L. A discrete element model (DEM) for predicting apple damage during handling[J]. Biosystems Engineering, 2018, 172: 29-48. DOI:10.1016/j.biosystemseng.2018.05.015 (  0) 0) |
| [21] |
于庆旭, 刘燕, 陈小兵, 等. 基于离散元的三七种子仿真参数标定与试验[J]. 农业机械学报, 2020, 51(2): 123-132. DOI:10.6041/j.issn.1000-1298.2020.02.014 (  0) 0) |
| [22] |
FAVIER J F, ABBASPOUR-FARD M H, KREMMER M, et al. Shape representation of axi-symmetrical, non-spherical particles in discrete element simulation using multi-element model particles[J]. Engineering Computations, 1999, 16(4): 467-480. DOI:10.1108/02644409910271894 (  0) 0) |
| [23] |
ABBASPOUR-FARD M H. Theoretical validation of a multi-sphere discrete element model suitable for biomaterials handling simulation[J]. Biosystems Engineering, 2004, 88(2): 153-161. DOI:10.1016/j.biosystemseng.2004.03.010 (  0) 0) |
| [24] |
KRUGGEL-EMDEN H, RICKELT S, WIRTZ S, et al. A study on the validity of the multi-sphere discrete element method[J]. Powder Technology, 2008, 188(2): 153-165. DOI:10.1016/j.powtec.2008.04.037 (  0) 0) |
| [25] |
SALOT C, GOTTELAND P, VILLARD P. Influence of relative density on granular materials behavior: DEM simulations of triaxial tests[J]. Granular Matter, 2009, 11(4): 221-236. DOI:10.1007/s10035-009-0138-2 (  0) 0) |
| [26] |
KOZHAR S, DOSTA M, ANTONYUK S, et al. DEM simulations of amorphous irregular shaped micrometer-sized titania agglomerates at compression[J]. Advanced Powder Technology, 2015, 26(3): 767-777. DOI:10.1016/j.apt.2015.05.005 (  0) 0) |
| [27] |
韩丹丹, 张东兴, 杨丽, 等. 内充气吹式玉米排种器工作性能EDEM-CFD模拟与试验[J]. 农业工程学报, 2017, 33(13): 23-31. DOI:10.11975/j.issn.1002-6819.2017.13.004 (  0) 0) |
| [28] |
原建博, 李骅, 吴崇友, 等. 基于离散单元法的水稻籽粒快速颗粒建模研究[J]. 南京农业大学学报, 2018, 41(6): 1151-1158. DOI:10.7685/jnau.201801004 (  0) 0) |
| [29] |
王美美, 王万章, 杨立权, 等. 基于EDEM的玉米子粒建模方法的研究[J]. 河南农业大学学报, 2018, 52(1): 80-84. (  0) 0) |
| [30] |
张涛, 刘飞, 赵满全, 等. 玉米秸秆接触物理参数测定与离散元仿真标定[J]. 中国农业大学学报, 2018, 23(4): 120-127. DOI:10.11841/j.issn.1007-4333.2018.04.15 (  0) 0) |
| [31] |
夏蕊, 杨兆建, 李博, 等. 基于离散元法的煤散料堆积角试验研究[J]. 中国粉体技术, 2018, 24(6): 36-42. (  0) 0) |
| [32] |
韩燕龙, 贾富国, 唐玉荣, 等. 颗粒滚动摩擦系数对堆积特性的影响[J]. 物理学报, 2014, 63(17): 173-179. (  0) 0) |
| [33] |
罗菊川, 文晟, 李涵光, 等. 甘蔗尾茎泊松比的试验分析[J]. 华南农业大学学报, 2017, 38(6): 118-124. DOI:10.7671/j.issn.1001-411X.2017.06.018 (  0) 0) |
| [34] |
罗菊川, 区颖刚, 刘庆庭. 甘蔗尾茎力学特性试验[J]. 农机化研究, 2016, 38(7): 220-223. DOI:10.3969/j.issn.1003-188X.2016.07.045 (  0) 0) |
| [35] |
刘庆庭, 区颖刚, 卿上乐, 等. 甘蔗茎秆在扭转、压缩、拉伸荷载下的破坏试验[J]. 农业工程学报, 2006, 22(6): 201-204. DOI:10.3321/j.issn:1002-6819.2006.06.043 (  0) 0) |
| [36] |
刘庆庭, 区颖刚, 袁纳新. 甘蔗茎在弯曲荷载下的破坏[J]. 农业工程学报, 2004, 20(3): 6-9. DOI:10.3321/j.issn:1002-6819.2004.03.002 (  0) 0) |
| [37] |
王美美. 单芽段甘蔗种植机排种机理与种植均匀性研究[D]. 广州: 华南农业大学, 2014.
(  0) 0) |
| [38] |
温翔, 杨望, 郭无极, 等. 切段式甘蔗收割机排杂离散元仿真参数标定及验证[J]. 中国农机化学报, 2020, 41(1): 12-18. (  0) 0) |
| [39] |
黄積佰. 切段式甘蔗收获机除杂系统的流固耦合仿真与优化[D]. 广州: 华南农业大学, 2020.
(  0) 0) |
 2022, Vol. 43
2022, Vol. 43


