随着智慧农业的快速发展，柑橘、荔枝、番石榴等季节性水果的采摘过程正往自动化方向转型^[1]，在非结构化环境下，果树自然生长形态呈无序性^[2]，机械臂采摘任务中存在树枝和非目标果实等障碍物，可能会发生碰撞。碰撞会降低水果质量和产量，并对机械臂和果树都可能造成损伤。因此，为实现水果无损高效的采摘，需要规划出可行的路径来保证机械臂在采摘的过程中尽量避开障碍物。

传统的机械臂路径规划算法有快速扩展随机数法^[3-5]、遗传算法^[6]、A*算法^[7]、栅格法^[8]、蚁群算法^[9-10]等。这些算法对于三维环境中的非结构化障碍物和多自由度机械臂来说，过于依赖环境的实时精确建模，且随着机械臂的自由度增加，算法的计算复杂度呈指数级增加，同时依赖参数设定，复杂环境下算法规划的计算时间较长，难以保证稳定性和可靠性。人工势场(Artificial potential field, APF)自1986年由Khatib^[11]首次提出以来，已被广泛应用于机械臂的避障。史亚飞等^[12]提出了一种基于改进的人工势场的运动规划方法，使机械臂能够在多障碍物环境下实现动态避障，但是障碍物的斥力势场产生的斥力仅作用于末端执行器，很难保证机械臂的其他部分与障碍物不发生碰撞。为了正确处理障碍物的斥力势场与整个机械臂之间的相互作用，一些研究集中在作用点的选择上。Wang等^[13]通过定义虚拟力与障碍物上最近点和关节的距离之间的关系来实现避障。上述运动规划方法均在笛卡尔空间中进行，每个规划步骤都需要逆运动学求解。然而，机械臂的逆运动学是一个复杂的多解问题，可能导致关节角路径不连续和奇异点的问题。谢龙等^[14]通过结合机械臂末端与障碍物最近点的排斥力来描述作用于机械臂的排斥力。Zhang等^[15]提出了一种改进的六自由度串行机器人运动规划的人工势场方法来解决这个问题，该规划直接在关节空间进行，以避免逆运动学求解，虽然这种方法不再需要求解逆运动学，但它在每一步中都需要大量的遍历，并且容易落入局部最小值，鲁棒性不强。

近年来，深度强化学习(Deep reinforcement learning, DRL)的快速发展给传统的人工势场法带来了更多的可能。深度强化学习通常基于几个神经网络作为预测操作的策略，通过与环境交互的方式获取数据，对获取的数据进行训练学习控制决策，在计算方面拥有更好的鲁棒性，从而管理一系列复杂的机械臂任务^[16-18]。采摘机械臂执行采摘作业任务可以抽象化为一个马尔可夫决策过程。因此对于非结构化环境下采摘机械臂的路径规划问题可以通过深度强化学习进行求解。深度强化学习中的深度确定性策略梯度算法(Deep deterministic policy gradient，DDPG)算法和软行为评判(Soft actor critic，SAC)算法可以应用于机械臂连续动作控制的领域。但是，采摘机械臂工作的非结构化环境复杂导致了网络的训练效率低。Lu等^[19]提出一种信息瓶颈理论，尽可能地限制从环境观测传递到状态标识的信息，鼓励神经网络去学习一些高维的特征，提升了算法的训练效果。DeepMind的研究者在文献[20]中提出一种结合了LSTM的改进架构(Contrastive bert for reinforcement learning，CoBERL)进行深度强化学习，以提高数据的处理效率。Lin等^[21]提出了一种结合了循环神经网络的DDPG算法，应用在番石榴采摘机器人上，获得了较好的鲁棒性。

本文以六自由度采摘机械臂在柑橘果树的非结构化环境中的路径规划问题为研究对象，基于深度强化学习算法进行研究。首先针对深度强化学习在非结构化环境中采摘路径规划成功率低的问题，提出一种结合人工势场的强化学习方法，让深度强化学习算法获得更高维的信息，通过仿真试验说明该方法可以提升路径规划的成功率。基于结合人工势场的强化学习方法，进一步引入LSTM结构，对包含Actor-critic网络的2种深度强化学习算法(DDPG和SAC)进行改进，通过仿真试验表明，改进后的算法的收敛速度和采摘路径规划成功率得到了显著提升。最后，与传统方法进行对比，结果表明所提出的基于SAC的改进算法在采摘路径规划耗时、路径规划长度和路径规划成功率方面具有优越性。

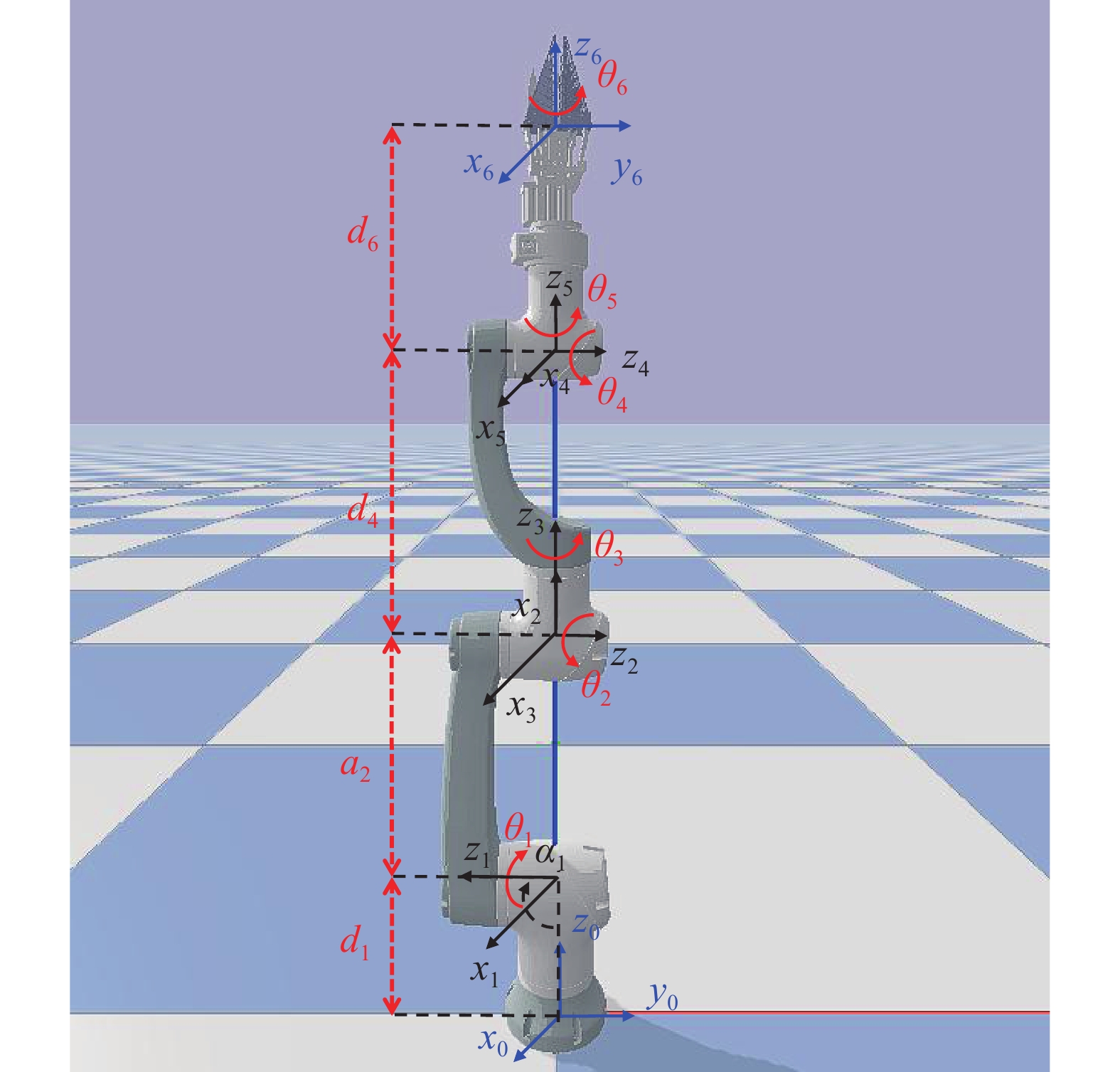
1 研究方法 1.1 采摘机械臂工作环境 1.1.1 采摘机械臂

本研究所采用的机械臂主体为Hans robot Elfin-5机械臂，由机械臂、爪型采摘末端执行器组成。机械臂包含6个连杆和6个转动关节。爪型采摘末端执行器连接到连杆6上，作为连杆6的一部分。根据标准Denavit-Hartenberg(D-H)方法建立机械臂连杆坐标系，如图1所示；采摘机械臂的D-H参数如表1所示。

1.1.2 碰撞检测和路径规划问题

在采摘机械收获目标果实的过程中，需要定义采摘点，一般有2种方式：一种对于葡萄、荔枝等串型水果，将采摘点定义在果串的末端以让执行器收获成串水果；另一种对于苹果、柑橘等单果球型水果，定义其质心作为采摘点以让执行器收获单个果实。对于单果球型的柑橘果实的采摘，取果实的质心作为采摘点以指导末端执行器到达采摘位置^[22-23]。将采摘任务路径规划过程简化为一个运动规划问题：将末端执行器从初始位置移动到采摘点位置。在检测末端执行器与采摘目标点位置时，若欧氏距离小于等于0.02 m则判定为到达。

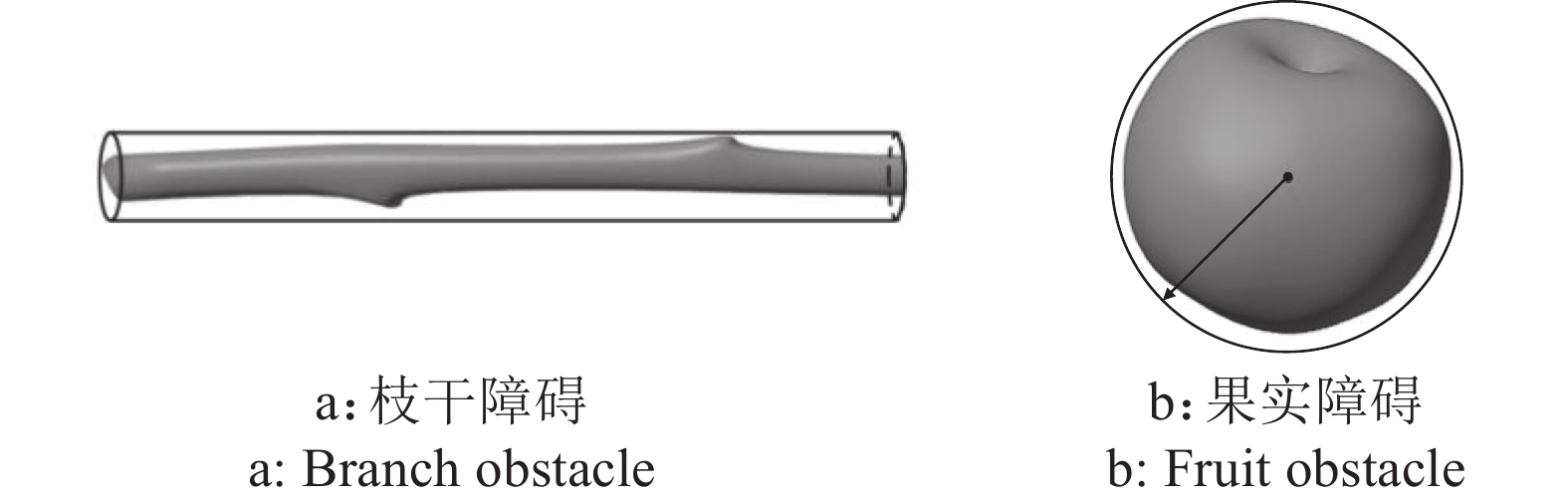
本文采用几何包络法实现障碍物的近似描述从而进行碰撞检测^[5,24-25]。因树叶具有良好的柔性，对机械臂采摘作业的影响很小，可以不计算树叶的碰撞^[26]。如图2所示，使用圆柱体包络表示枝干障碍，使用球体包络表示非目标果实障碍。对于目标果实，不采取碰撞检测，而使用采摘点作为近似替代。

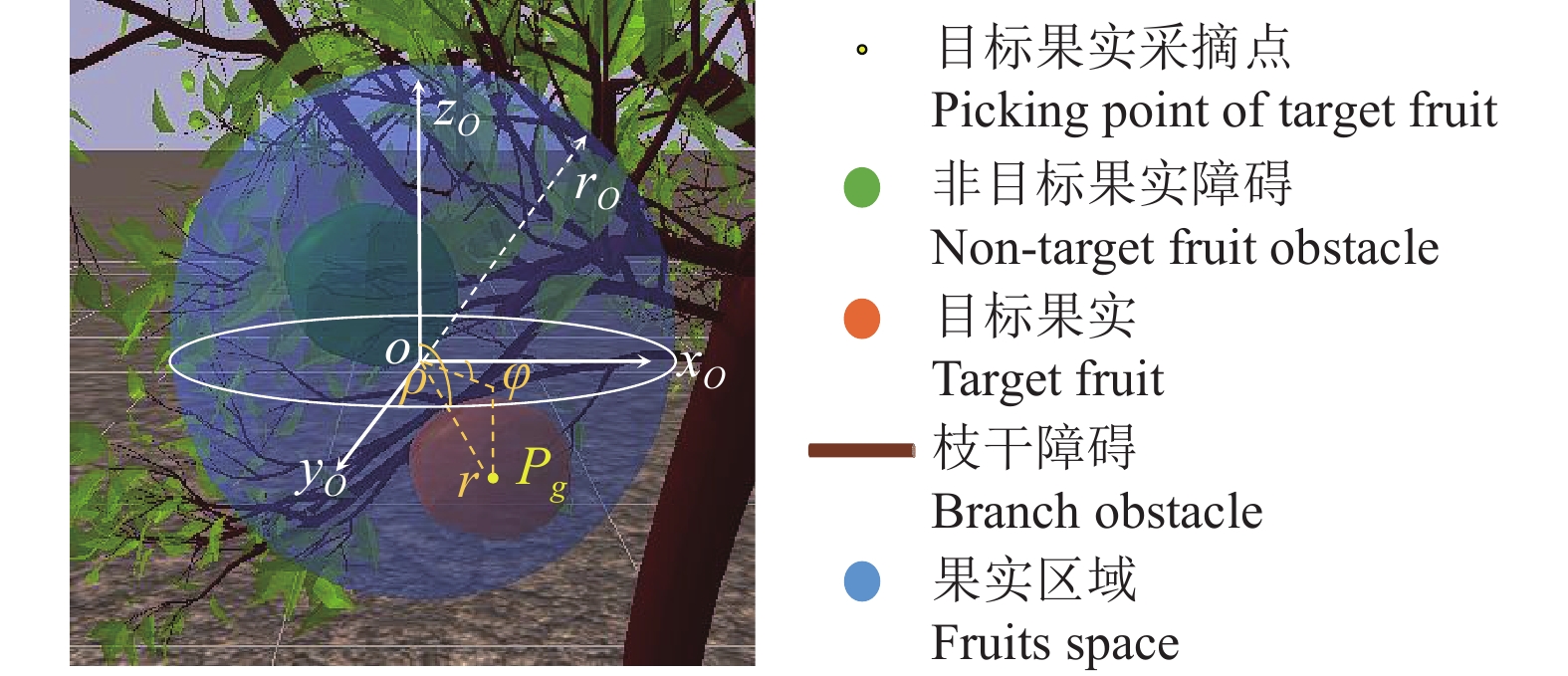
果实的位置应根据柑橘的疏花疏果操作^[27]，综合考虑机械臂位置及障碍物的位置以及机械臂有效工作范围进行合理设置。如图3所示，将果实区域限定在树枝末梢附近。果实区域 $ O( {x_O},{y_O},{z_O}, {r_O} ) $ 是以O为原点，半径为 $ {r_O} $ 的球体，其中 $ {r_O} $ 取0.08 m。在果实区域中以O为原点建立球极坐标系，非目标果实的质心和目标果实的采摘点以球极坐标 ${p_g}\left( {r,\varphi ,\rho } \right)$ 的形式表示，其中，根据正态分布 $ r\sim N(0.04,{0.5^2}) $ 的方式生成径向距离r，使用Python中random函数随机取值的方式生成方位角φ和极角ρ。

1.1.3 采摘平面定义

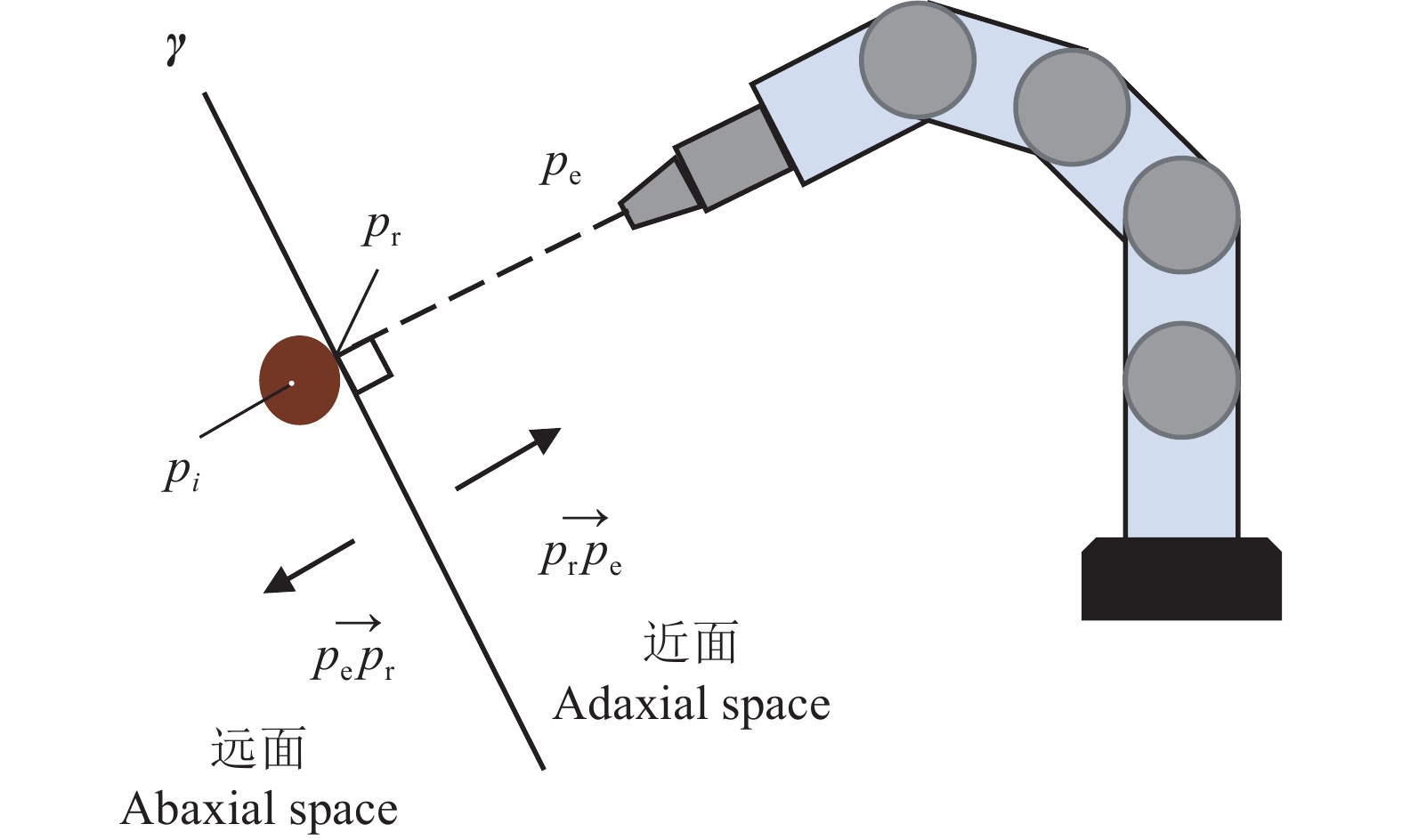
为描述果实、枝干与机械臂的空间位置关系^[28]，引入采摘平面的概念。如图4所示，对枝干的圆形横截面中心点 $ {p_i} $ 与末端执行器 ${p_{\rm{e}}}$ 进行连线，线段 ${p_i}{p_{\rm{e}}}$ 与枝干的横截面圆形交点为 ${p_{\rm{r}}}$ ，则于 ${p_{\rm{r}}}$ 可作一个与 ${p_i}{p_{\rm{e}}}$ 垂直的切平面γ，将该切平面γ称作采摘平面。定义向量 $\overrightarrow {{p_{\rm{r}}}{p_{\rm{e}}}} $ 为γ到末端执行器方向的空间向量，以γ为分界平面，该方向上的空间定义为近面；相反地，以γ为分界，向量 $\overrightarrow {{p_{\rm{e}}}{p_{\rm{r}}}} $ 所表示方向的空间为远面。根据位置关系可以推断出：当机械臂需要到达位于远面上的目标时，路径规划中需要对枝干进行避障。

1.1.4 采摘试验环境搭建

PyBullet是基于Bullet物理引擎的一款仿真器，通过Python连接深度强化学习算法。本文选择PyBullet搭建仿真采摘环境，进行机械臂运动仿真测试，如图5所示。试验中设定了3种采摘环境，3种环境中树枝和果实分布位置不同。在机械臂可达的空间内设置果实区域，引用“1.1.3”中对采摘平面以及近面、远面的定义可以对3种环境描述如下：环境A中的果实区域均位于采摘平面的近面上，在起始情况下从 ${p_{\rm{e}}}$ 到采摘点 ${p_{{g}}}$ 的空间内只存在细小分枝和非目标果实障碍，因此机械臂能够以更小的难度到达采摘点，并且果实分布更加密集。环境B中设置了更多的主枝障碍，其中80%的果实区域位于远面，机械臂的运动范围中的障碍包括主枝、分枝和非目标果实，相较于环境A更复杂，难度更大。环境C中，20%的果实区域在远面上，在机械臂的初始位姿正前方较近的位置存在一根需要避障的主枝，且工作环境相对狭窄。

环境A中机械臂和果树的基座标分别为(0,0,0.75)和(0.25,−1.70,0)；环境B中机械臂和果树的基座标分别为(0,−0.30,0.75)和(0,1.30,0)；环境C中机械臂和果树的基座标分别为(0,0,0.75)和(−1.00,−1.20,0)。

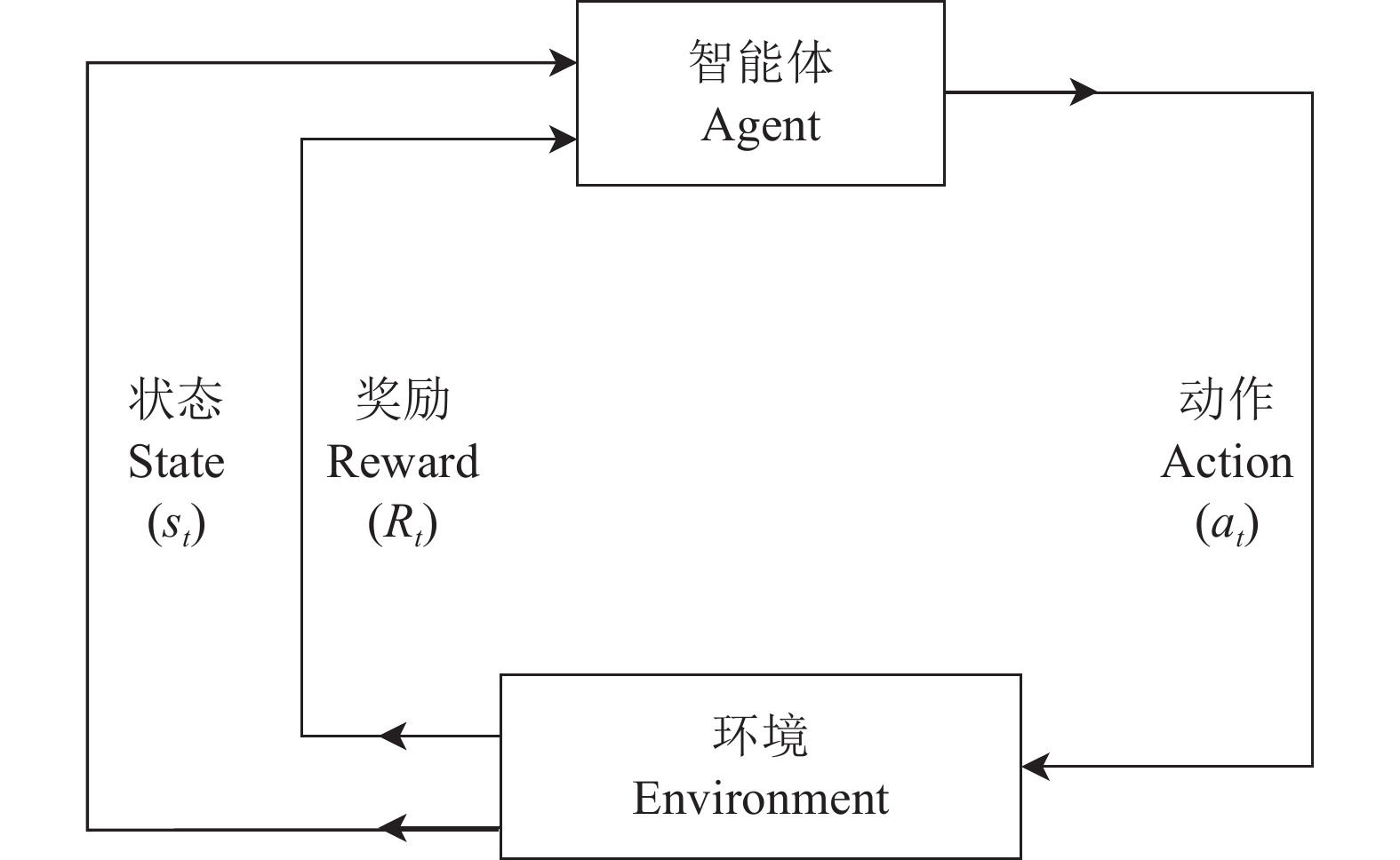
1.2 强化学习设计

在机械臂执行采摘任务的过程中，机械臂的状态与动作之间存在映射关系，即下一个状态取决于当前状态和当前动作，可以用马尔可夫决策过程(Markov decision process，MDP)进行建模。此过程主要分为4个部分，即状态集合S、动作集合A、状态转移概率P和奖励回报R。在运动路径规划过程中机械臂作为智能体，在某一时刻t，机械臂的姿态以及与周围障碍物的位置关系都会对应一个状态 $ {s_t} $ ，机械臂根据策略 $ \pi ({s}_{t}) $ 以概率 $ P({s_{t + 1}}|{s_t}) $ 选择动作 $ {a_t} $ ，执行动作 $ {a_t} $ 之后，机械臂的姿态以及与周围障碍物的位置关系将会进入一个新的状态 $ {s_{t + 1}} $ ，机械臂得到奖励 $ {R_t} $ 。智能体在这样的交互中不断更新自己的策略模型，直至学习到满足任务要求的最优策略模型。智能体与环境之间的交互关系流程如图6所示。

1.2.1 基于人工势场法的状态空间

人工势场是一种局部路径规划的方法，通过人工势场辅助机械臂进行避障，其基本思想是：目标点对机械臂产生引力作用，障碍物对机械臂产生斥力作用，引力和斥力的合力方向决定机械臂的运动方向。为了让智能体获取更多的环境信息，本研究结合了人工势场法对状态信息进行设计。下文中，结合人工势场的状态记为 $ {s_{{\text{APF}}}} $ ，不含人工势场法的基础状态记为 $ {s_{{\text{basic}}}}$ 。

对于采摘机械臂在非结构化环境下工作可获取的状态信息，可以分类为障碍物位置信息、机械臂姿态信息。文献[29-32]对于机械臂在非结构化环境下工作的研究中，基础状态空间的设计主要基于机械臂姿态、目标位置、障碍物位置、机械臂与障碍物之间的距离、末端与障碍物之间的距离。如式(1)设计基础状态 $ {s_{{\text{basic}}}} $ ：

$ \left\{ \begin{gathered} {s_{\text{r}}} = [{\theta _n},{p_{\rm{e}}},{d_g}] \\ H_i = [{p_i},{d_{ni}}] \\ {s_{{\text{basic}}}} = \{ {p_g},{s_{\text{r}}},H_i\} \end{gathered} \right.，$

(1)

式中， $ {s_{\text{r}}} $ 为机械臂状态， ${H_i}$ 为障碍物 $ i $ 状态。 ${\theta _n}$ 为机械臂 $ n $ 轴的角度， $ {p_{\rm{e}}} $ 表示机械臂末端位置。 $ {d_g} $ 表示机械臂末端与目标的距离， $ {p_i} $ 表示障碍物位置， $ {d_{ni}} $ 表示机械臂 $ n $ 连杆与障碍物 $ i $ 的距离， ${p_g}$ 表示目标位置。

将采摘点、障碍物和机械臂的部分状态用人工势场描述。考虑到机械臂工作环境下的距离特点，构建目标点g的引力势场U_g和障碍物 $ i $ 对机械臂 $ n $ 连杆的斥力势场U_ni：

$ {U_g}({d_g}) = \dfrac{1}{2}\xi d_g^2 ，$

(2)

$ {U_{ni}}({d_{ni}}) = \left\{ {\begin{array}{*{20}{l}} {\dfrac{1}{2}\eta {{\Bigg(\dfrac{1}{{10{d_{ni}}}} - \dfrac{1}{{10{d_{\text{m}}}}}\Bigg)}^2}, }&{ {d_{ni}} \leqslant {d_{\text{m}}}} ，\\ {0, }&{{d_{ni}} > {d_{\text{m}}} }，\end{array}} \right. $

(3)

式中， $ \xi $ 为引力参数， $ \eta $ 为斥力参数， ${d_{\text{m}}}$ 表示障碍物的影响半径。根据式(2)和式(3)，将人工势场加入机械臂状态s_r和障碍物 $ i $ 状态 ${H_i} $ 中，得到 $s{'_{\rm{r}}} $ 和 $ H{'_i} $ ，进而构建人工势场状态 $ {s_{{\text{APF}}}} $ ：

$ \left\{ \begin{gathered} s{'_{\rm{r}}} = [{\theta _n},{p_{\rm{e}}},{d_g},{U_g}] \\ H{'_i} = [{p_i},{d_{ni}},{U_{ni}}] \\ {s_{{\text{APF}}}} = \{ {p_g},s{'_{\rm{r}}},H{'_i}\} \end{gathered} \right.。$

(4)

1.2.2 奖励函数与动作空间

在采摘作业任务中，机械臂需要准确避开障碍物，并驱动末端执行器尽量以最短的时间到达采摘目标点，因此需要设置一种合理的奖励策略。一般地，在奖励设定时，设置负奖励的目的是避免某情况的发生，正奖励的目的是希望得到某个结果。首先基于前述的基本状态和参考文献[30-32]中描述的避障奖励方法进行奖励设定，具体如公式(5)的basic方法。

$ \begin{split} & {R_{{\text{basic}}}} = {R_{\text{a}}} + {R_{\text{c}}} + {R_{{\text{step}}}} ，\\ & {R_{\text{a}}} = \left\{ {\begin{array}{*{20}{l}} {- (0.5d_g^2{\text{), }} }&{ {d_g}{\text{ < }}\delta }，\\ { - [\delta (\left| {{d_g}} \right| - 0.5\delta )], }&{{d_g} \geqslant \delta }，\end{array}} \right. \\ & {R_{\text{c}}} = \left\{ {\begin{array}{*{20}{l}} { 0, }&{{d_{ni}} > 0 }，\\ { - 10, }&{{d_{ni}} = 0 }，\end{array}} \right.\\ & {R_{{\text{step}}}} = \dfrac{{{\tau _1}}}{{{t_{{\text{step}}}}}} ，\end{split} $

(5)

式中，R_a为平滑距离奖励， $\delta $ 为平滑参数，R_c为避障奖励，R_step为步数奖励， ${\tau _{\text{1}}}$ 为步数奖励常数， ${t_{{\text{step}}}}$ 为该回合内的仿真时间步长。

对人工势场方法的奖励R_APF进行设定，使用公式(2)的引力势场函数构建目标引导奖励函数R_att，使用公式(3)的斥力势场构建避障奖励函数R_rep。

$ \begin{split} & {R_{{\text{att}}}}({d_g}) = \left\{ {\begin{array}{*{20}{l}} { {\tau _2}[{U_0} - {U_g}({d_g})], }&{ {d_g} > 0 }，\\ { {\tau _3}, }&{{d_g} = 0 }，\end{array}} \right.\\ & {R_{{\text{rep}}}}({d_{ni}}) = \left\{ {\begin{array}{*{20}{l}} { {\tau _4}{U_{ni}}({d_{ni}}), }&{{{d_{ni}} > 0} }，\\ { {\tau _5},}&{ {{d_{ni}} = 0} }，\end{array}} \right. \end{split} $

(6)

式中， $ {U_0} $ 为末端位于初始位置的引力势场，末端离采摘点越近，奖励越大。 ${\tau _2}$ 、 ${\tau _3}$ 均为正值，当距离d_g=0时，说明末端已到达采摘点，完成采摘任务，给予一个高值奖励。 ${\tau _4}$ 、 ${\tau _{\text{5}}}$ 取负值，触发在斥力范围内工作的情况会给出一定的惩罚。如果在此过程中发生碰撞的情况，则给予一个高值的负奖励。

综上所述，总奖励为目标引导奖励函数、避障斥力函数、步长奖励函数的累计，如公式(7)所示。

$ {R_{{\text{APF}}}} = {R_{{\text{att}}}} + \displaystyle\sum\limits_{i = 0}^n {{R_{{\text{rep}}}}({d_{ni}}) + {R_{{\text{step}}}}}。$

(7)

基于关节空间定义机械臂的动作空间A：

$ A = [{\theta _1},{\theta _2},{\theta _3},{\theta _4},{\theta _5},{\theta _6}]，$

(8)

式中， $ {\theta }_{1}、{\theta }_{2}、{\theta }_{3}、{\theta }_{4}、{\theta }_{5}、{\theta }_{6} $ 分别为机械臂1、2、3、4、5、6轴的关节角度。

1.3 Actor-critic算法

行为−评判算法(Actor-critic algorithm)是一种结合策略网络和价值函数的深度强化学习算法，Actor为行为网络，使用策略梯度算法，负责生成动作，并与环境交互，一般用神经网络实现，输入是当前状态，输出是动作。该网络的训练目标是最大化累计回报的期望。Critic为评判网络，使用价值函数Q，负责评价Actor的表现，并指导Actor后续行为动作，同样可以通过神经网络实现，该网络可以对当前策略函数进行估计，可以评价策略函数Actor的好坏。本研究中使用2种主流的基于Actor-critic算法的深度强化学习算法——DDPG和SAC进行机械臂的路径规划。

1.3.1 深度确定性策略梯度算法

深度确定性策略梯度^[33](Deep deterministic policy gradient，DDPG)算法结合深度Q网络(Deep Q network, DQN)算法的原理引入了神经网络，不仅可用来解决基于高维连续动作空间的强化学习问题，而且使得值函数收敛问题也得到了很好的解决。训练过程中，一共有4个神经网络，即Actor网络、Target actor网络、Critic网络和Target critic网络，分别对应：行为网络、目标行为网络、评判网络和目标评判网络。每个学习步骤完成后，将Actor网络和Critic网络中的参数分别复制到Target actor网络和Target critic网络中。因此，Actor网络和Target actor网络的架构必须完全相同，Critic网络和Target critic网络的架构必须完全相同。DDPG算法中 $ {\phi _{\text{a}}} $ 和 $ {\phi _{\text{c}}} $ 分别表示Actor和Critic的神经网络参数。在DDPG算法的训练过程中，根据公式(9)进行参数更新。

$ \begin{gathered} {\phi _{\text{a}}}' = \lambda {\phi _{\text{a}}} + (1 - \lambda ){\phi _{\text{a}}}'，\\ {\phi _{\text{c}}}' = \lambda {\phi _{\text{c}}} + (1 - \lambda ){\phi _{\text{c}}}'，\\ \end{gathered} $

(9)

式中， $ \lambda $ 为目标平滑因子，它影响目标网络的更新速度和智能体的学习稳定性。时间步状态估计误差y(t)由公式(10)计算。损失函数L由公式(11)通过梯度下降法最小化，其中T为累计训练步数。

$ y(t) = R({s_t},{a_t}) + \gamma \max Q({s_{t + 1}},{a_{t + 1}}) - Q({s_t},{a_t})，$

(10)

$ L = \dfrac{1}{T}\displaystyle\sum\limits_{t = 1}^T {{{\left[ {R({s_t},{a_t}) + \gamma \max Q({s_{t + 1}},{a_{t + 1}}) - Q({s_t},{a_t})} \right]}^2}}。$

(11)

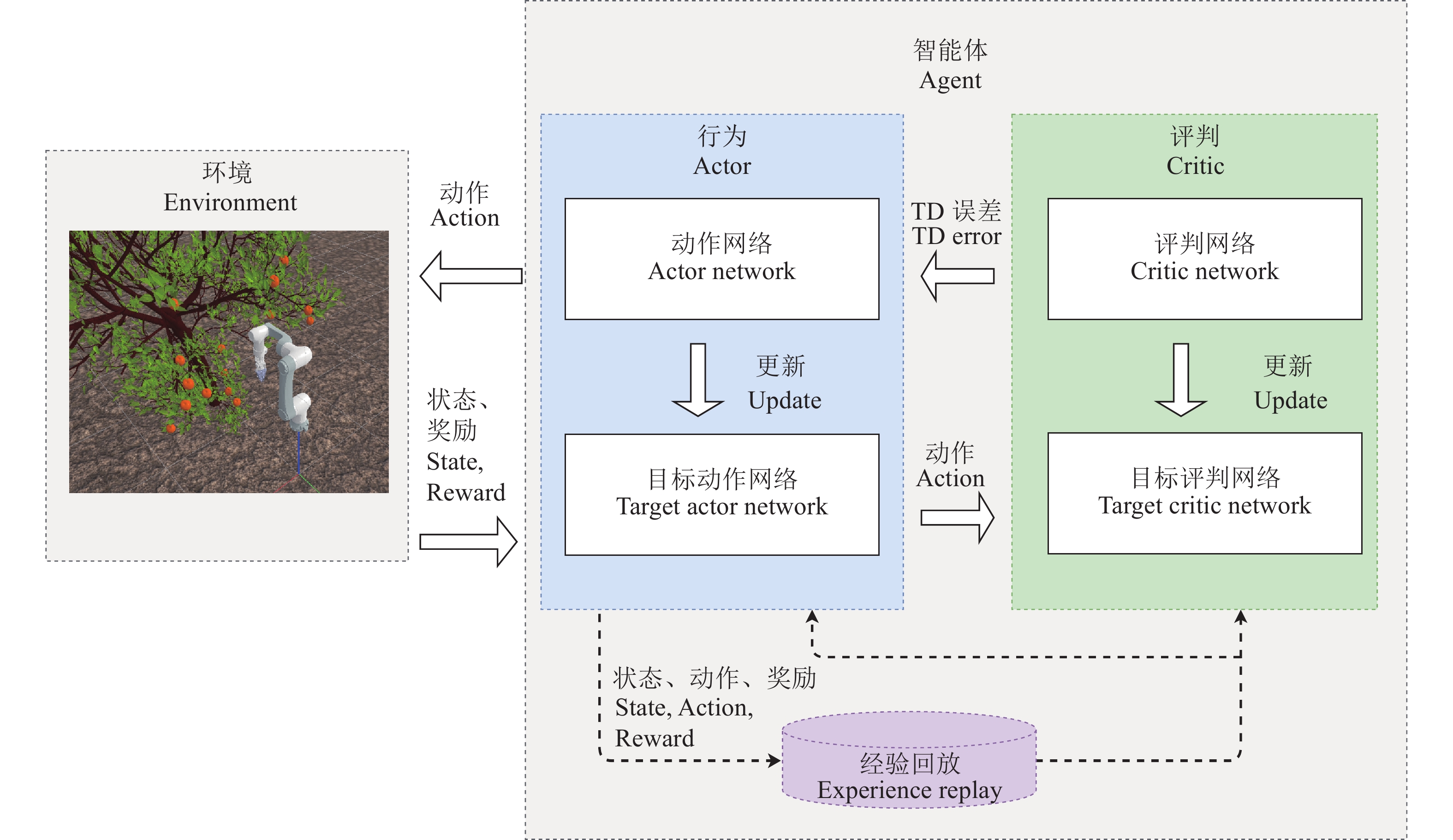
构建的深度强化学习DDPG网络如图7所示。

1.3.2 软行为评判算法

软行为评判(SAC)算法^[34-35]是一种以离线学习方式更新优化随机策略的算法，与DDPG算法相比，该算法训练的是一种随机策略，适用于涉及连续动作的强化学习任务。熵正则化是SAC的一个创新点，该策略经过训练，以权衡最大化预期回报和熵之间的关系，熵是衡量策略随机性的一个指标。熵增加时，会发生更多的探索。因此，可能加快学习，还可以避免过早收敛到局部最优。SAC的目标函数包括奖励项和熵 $ \mathcal{H} $ ，同时熵由温度参数α_temp进行加权，目标函数 $ J(\pi ) $ 的定义如公式(12)所示，熵函数定义如公式(13)所示。

$ J(\pi ) = \displaystyle\sum\limits_{t = 0}^T {{{E}_{({s_t},{a_t})\sim {\rho _\pi }}}\{R({s_t},{a_t}) + {\alpha _{{\text{temp}}}}\mathcal{H}[\pi ( \cdot |{s_t})]\}}，$

(12)

$ \mathcal{H}[\pi ( \cdot |{s_t})] = - \displaystyle\sum\limits_{{a_t}} {\pi ({a_t}|{s_t})\ln \pi ({a_t}|{s_t})} ，$

(13)

式(12)中，α_temp值越大，策略的随机性越强。 $ {{E}} $ 代表期望， $ {\rho _\pi } $ 表示策略的状态分布和状态作用边缘。SAC致力于学习3种功能： $ {\pi _{{\phi _{\text{a}}}}}({s_t},{a_t}) $ 与神经网络参数 $ {\phi _{\text{a}}} $ 、软动作值函数 $ {Q_{{\phi _{\text{c}}}}}({s_t},{a_t}) $ 与神经网络参数 $ {\phi _{\text{c}}} $ 、软状态值函数 $ {V_\psi } $ 。由于 $ {V_\psi } $ 可以由Q和 $ \pi $ 导出，原则上不需要为状态值单独设置函数逼近器。

在大多数情况下，决定训练成功与否的温度参数α_temp很难确定。然而，由于奖励的不断变化，使用固定的α_temp是不合理的，这会使整个训练不稳定，失去SAC对超参数依赖性低的优势。因此，我们希望神经网络能够自动调整α_temp的大小，以确保α_temp在不同状态下可以调整到不同的值。当某一状态达到最优策略时，α_temp逐渐收敛。我们可以用熵作为约束来求解策略和α_temp的优化问题。

$ \max {{E}_{{\rho _\pi }}}\left[ {\displaystyle\sum\limits_{t = 0}^T \text{π}{R({s_t},{a_t})} } \right],{\text{ s.t. }}\forall t,\mathcal{H}({\pi _t}) \geqslant {\mathcal{H}_0}，$

(14)

式中， $ {\mathcal{H}_0} $ 为最小熵阈值。基于上述约束优化问题，可得到如公式(14)所示的α_temp的目标函数。

$ J({\alpha _{{\text{temp}}}}) = {{{E}}_{{a_t}\sim {\pi _t}}}[ - {\alpha _{{\text{temp}}}}\ln {\pi _t}({a_t}|{s_t}) - {\alpha _{{\text{temp}}}}{\mathcal{H}_0}] 。$

(15)

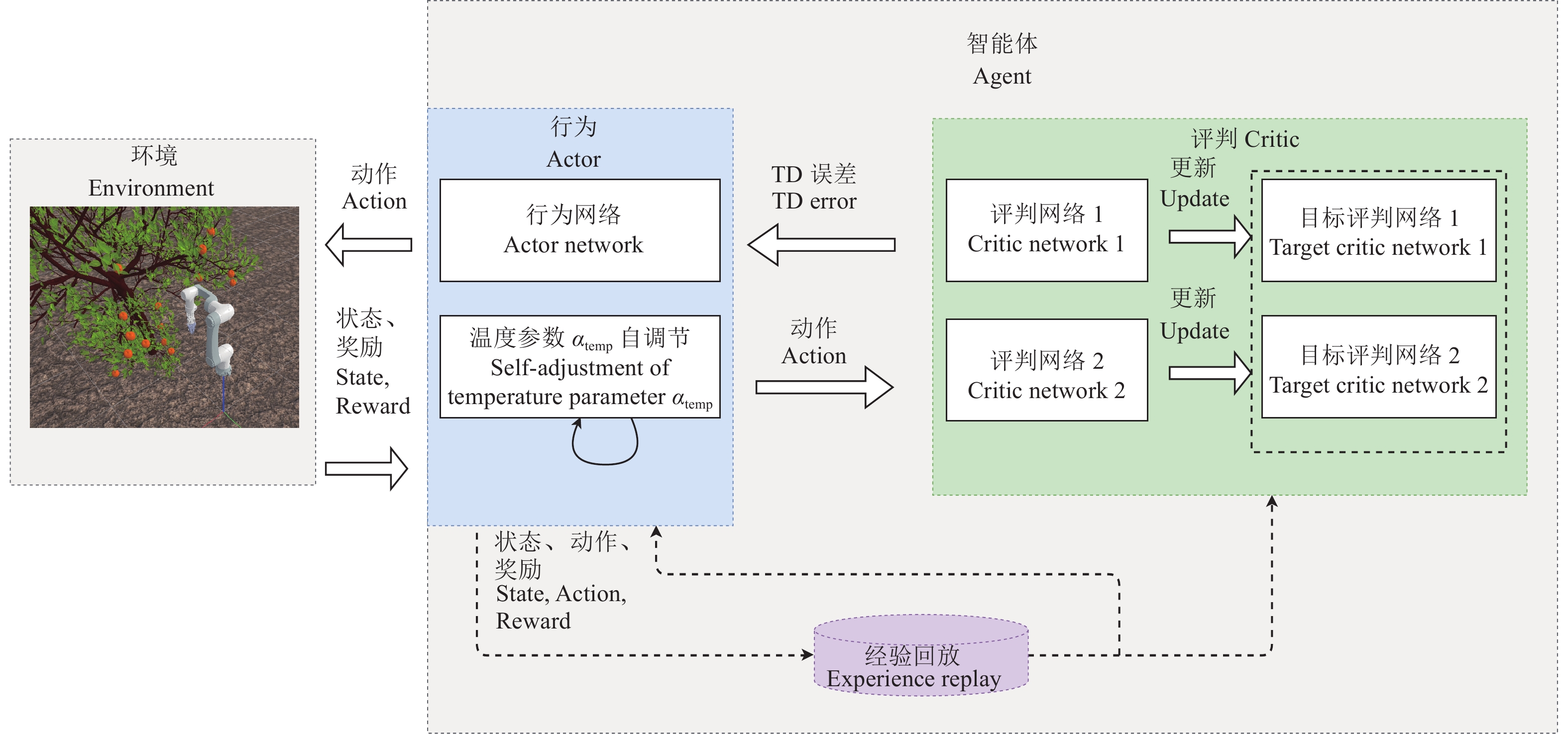
构建的深度强化学习SAC网络如图8所示。

1.4 结合LSTM的Actor-critic网络改进

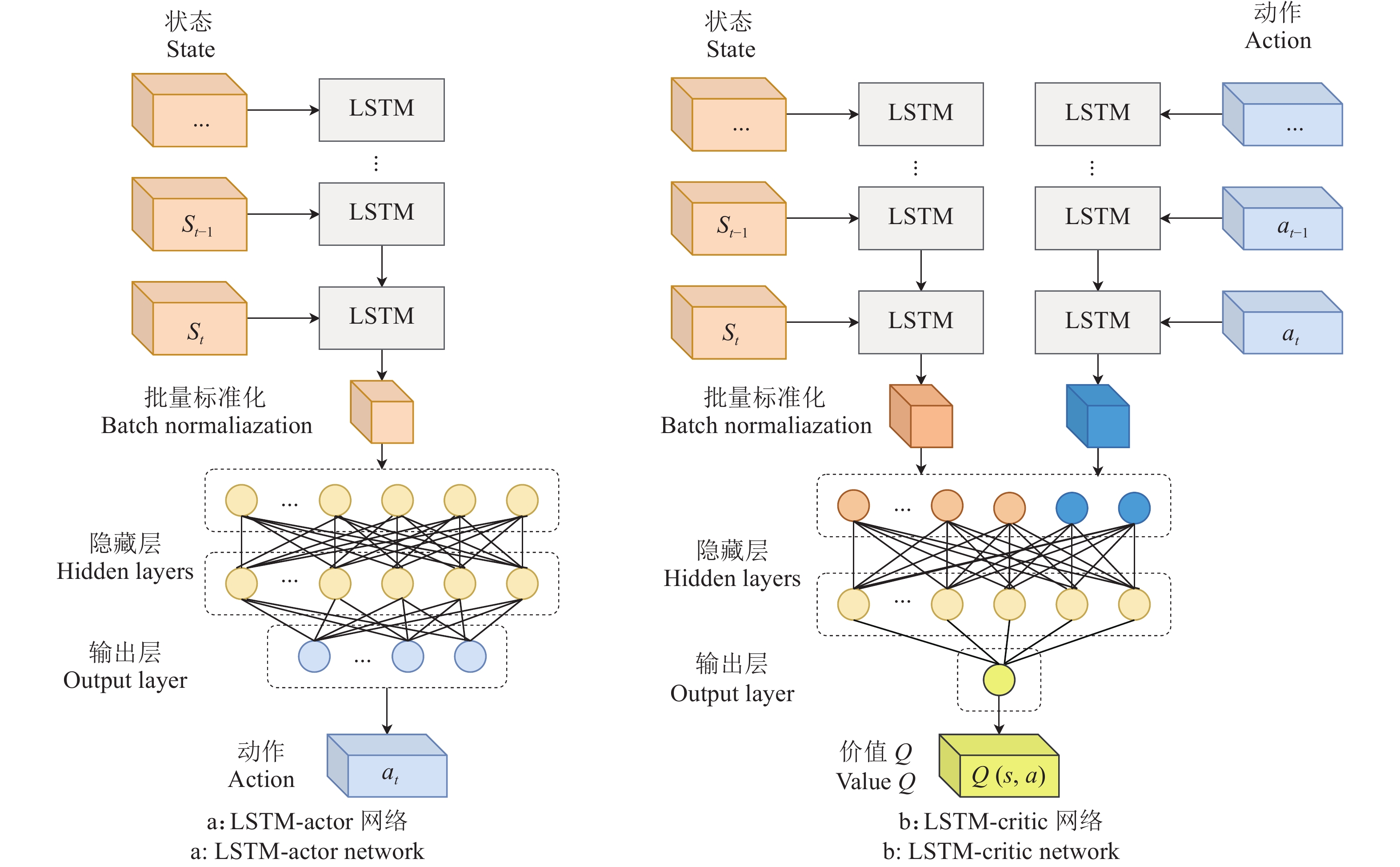
由于机械臂执行任务中与环境的关系具有时间序列特征，其路径规划过程不仅与当前时刻的状态有关，还与历史运动信息有关。智能体在充分认知环境的前提下，还需要学习足够多的运动前后关系才能获得更好的鲁棒性。本研究采用LSTM结构处理时序关系。LSTM网络有时间步长，将状态向量中属于不同时刻的状态向量 $ {s_t} $ 馈入LSTM的不同时间步长中。LSTM最后一个时间步长的输入向量是 $ {s_t} $ ，而前一个时间步长的输入向量是 $ {s_{t - 1}} $ ，以此类推进行输入。图9a为LSTM-actor网络结构，LSTM的输出被输入到一个全连接的深度神经网络(Deep neural network，DNN)中，该DNN生成一个动作 $ {a_t} $ ，然后根据Critic网络来估计动作的Q值。图9b为LSTM-critic网络结构，它的输入是状态 $ {s_t} $ 和动作 $ {a_t} $ ，LSTM用于提取状态 $ {s_t} $ 的特征，动作向量 $ {a_t} $ 也同样通过LSTM进行状态提取，二者的输出通过特征归一化后输入到全连接的DNN。此全连接的DNN负责学习从每个状态−动作到Q值的映射。

2 试验验证与结果分析

为验证方法的有效性，基于PyBullet搭建仿真试验平台，在3种不同难度的采摘环境下进行柑橘采摘机械臂的路径规划试验。试验主机基于Windows10操作系统和Python3.7语言，硬件配置为Intel Core I7 11700K，Nvidia RTX 3090和RAM 32 GB。在仿真试验中，人工势场的参数 $ \xi $ 、 $ \eta $ 、 $ {d_m} $ 和 $ \delta $ 分别设置为−1.0、1.0、0.5和0.5；奖励函数的参数 ${\tau _1}$ 、 ${\tau _2}$ 、 ${\tau _3}$ 、 ${\tau _4}$ 和 ${\tau _5}$ 分别设置为10、10、100、−1和−10。

2.1 人工势场有效性试验

基于SAC算法进行试验，将结合人工势场设计的方法记作APF方法，对应的状态和奖励分别为 $ {s_{{\text{APF}}}} $ 和 $ {R_{{\text{APF}}}} $ ；不含人工势场的方法记作basic方法，对应的状态和奖励分别为 $ {s_{{\text{basic}}}} $ 和 $ {R_{{\text{basic}}}} $ ，2种方法均基于前述的动作空间A进行试验。在3种环境中分别执行基于APF训练方法和basic训练方法的深度强化学习算法，每个环境中执行5×10⁵集迭代训练，深度强化学习神经网络的学习率设置为0.001，学习开始轮数设置为1000，batch_size参数选取512，强化学习折扣率设置为0.95，神经网络目标平滑因子 $ \lambda $ 取0.005。为直观分析训练效果，在学习过程中定期评估100次测试中采摘路径规划的成功率，并以它为评价指标进行分析。

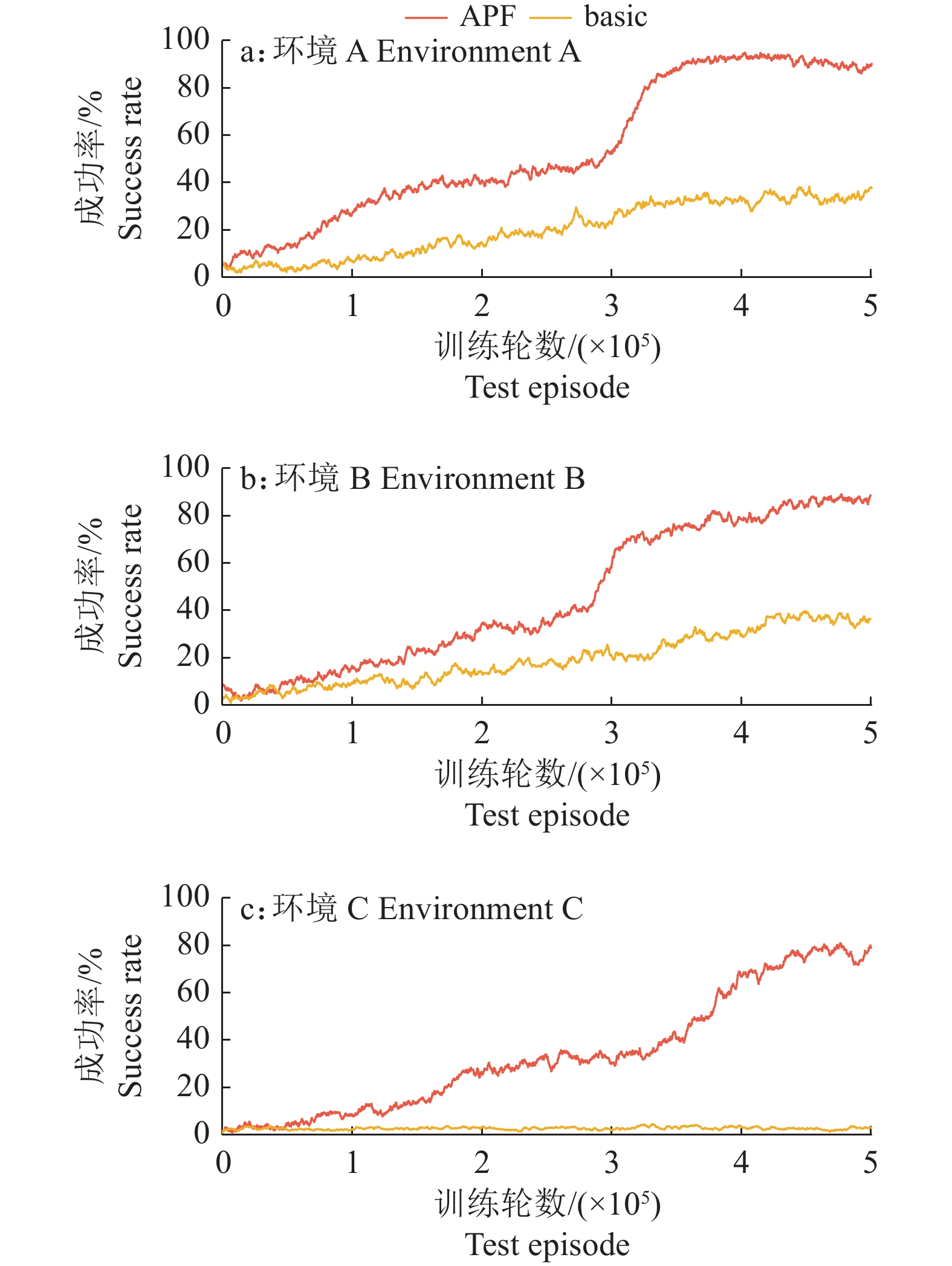
图10显示了在环境A、B和C试验中不同方法训练的SAC算法的采摘路径规划的成功率，可以发现，基于APF方法训练的采摘路径规划成功率高于basic方法。

在环境A和B中，训练曲线的变化趋势大体相似。在训练初期，APF方法的上升幅度高于basic。之后在3×10⁵集左右，APF方法训练的效果出现大幅提升，远超过basic方法。基于basic方法训练的算法在环境A和环境B中的成功率分别为38%和36%，而基于APF方法训练的算法的路径规划成功率更高，在环境A和环境B中分别达到90%和88%。在环境A中，APF方法的成功率出现了回落，随着训练次数的增加，降低的情况更加严重，不利于算法获得更好的性能。这是因为，在避障问题中进行更多的探索并不能解决动作价值高估的问题，使算法陷入了局部最优问题。在环境C中，basic方法无法完成任务，APF方法的收敛速度略慢于前2个环境，在4×10⁵集左右才开始收敛，并且震荡幅度相较于前2个环境更大，最终成功率为79%。

从对比试验可知，结合人工势场法后，智能体可以获取更多的环境信息，使深度强化学习算法尽可能学习策略以完成采摘点路径规划的任务。

2.2 基于LSTM结构的改进算法的有效性试验

试验对基于LSTM结构的改进DDPG和SAC算法的有效性进行分析。将机械臂规划任务强化学习问题看作是一个与时间序列相关的任务，引入LSTM结构处理时间序列的状态−动作信息，对DDPG和SAC算法的Actor网络和Critic网络进行改进。

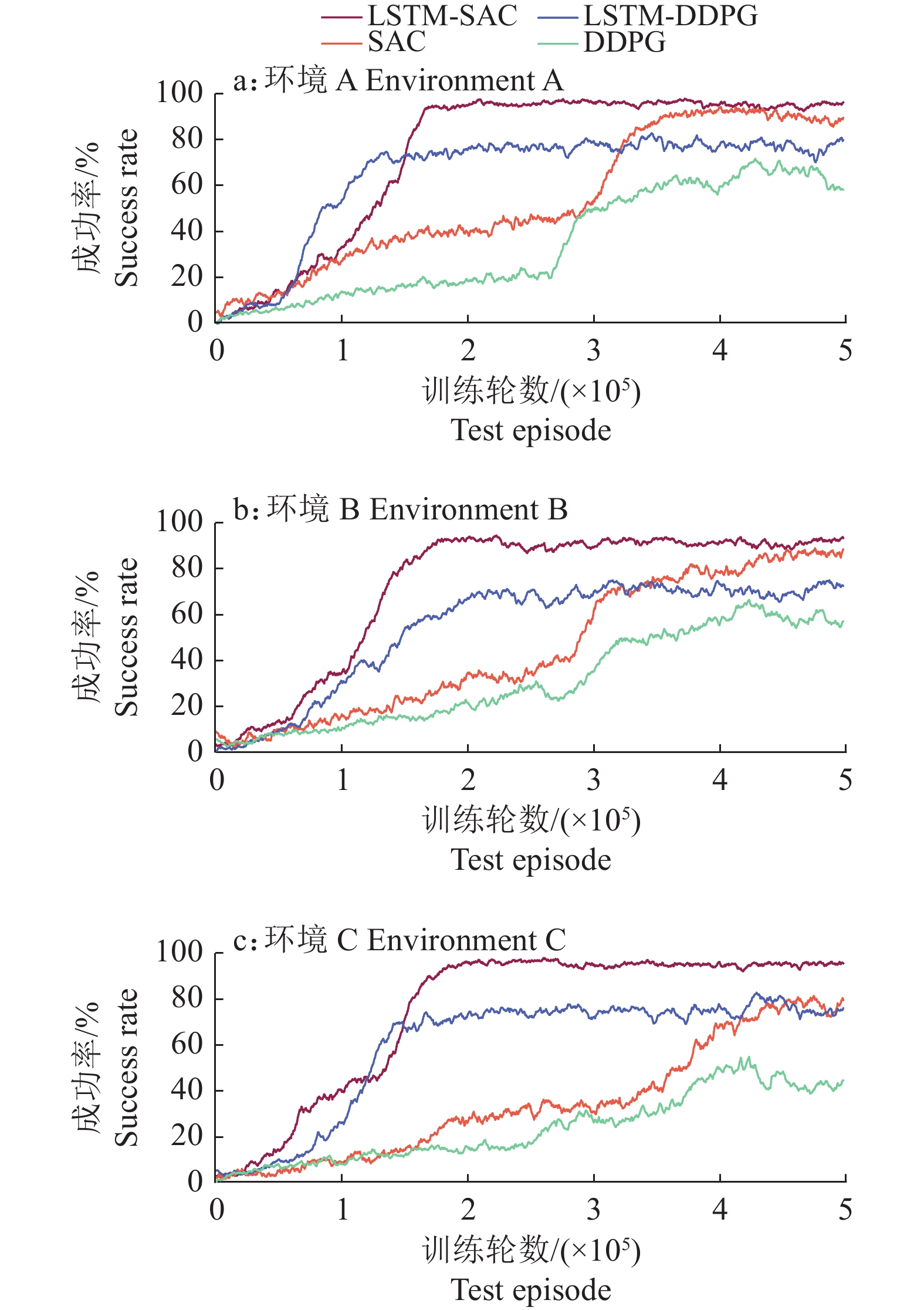
试验同样基于环境A、B和C，每个环境中执行5×10⁵集迭代训练，在学习过程中定期评估100次测试的采摘路径规划成功率，并将它作为评价指标进行分析。沿用“2.1”中的深度强化学习算法训练参数，将包含LSTM结构的2种改进算法分别记作LSTM-DDPG和LSTM-SAC，试验所得不同算法在不同环境下的采摘路径规划成功率情况如图11所示。

由图11可知，加入LSTM结构后，算法在收敛速度和路径规划成功率方面均得到提升。一方面，在3种采摘环境的试验中，DDPG及其改进算法收敛后的波动幅度均大于SAC及其改进算法。因此在训练效果稳定性方面，SAC及其改进算法优于DDPG及其改进算法。另一方面，在3种环境中，DDPG算法在训练的后期都出现了回落的情况，而SAC算法只在环境A中出现这种情况。这说明改进算法可以有效解决动作价值高估的问题，从而避免陷入局部最优的情况。

在环境A中，LSTM-SAC、LSTM-DDPG、SAC和DDPG算法的收敛点分别是1.780×10⁵、1.580×10⁵、3.760×10⁵和4.035×10⁵，环境B中，4个算法的收敛点分别是1.765×10⁵、2.115×10⁵、3.855×10⁵和4.085×10⁵，环境C中，4个算法的收敛点分别是1.910×10⁵、1.410×10⁵、4.180×10⁵和3.780×10⁵。在环境A、B和C中，与原算法对比，LSTM-SAC算法的采摘路径规划成功率分别提升了6%、5%和16%，综合提升了9%，算法收敛速度分别提升了52.66%、54.21%和54.31%，综合提升了53.73%。LSTM-DDPG算法的采摘路径规划成功率分别提升了22%、15%和32%，综合提升了23%，算法收敛速度分别提升了60.84%、48.22%和62.70%，综合提升了57.25%，且算法规避了局部最优情况的发生。DDPG算法在该任务上存在更大的提升空间，因此本文提出的改进方法在DDPG算法上对路径规划成功率的提升幅度大于SAC，相对地，SAC在该任务上拥有更好的鲁棒性，提升空间更小。另外，本研究结果表明，SAC及其改进算法LSTM-SAC在该任务中的表现效果分别优于DDPG算法及其改进算法LSTM-DDPG。

2.3 路径规划效果对比

为了进一步量化分析算法对采摘机械臂路径规划的效果，本节在3种采摘试验环境下分别测试100次LSTM-SAC、LSTM-DDPG、SAC和DDPG算法对采摘路径进行规划的平均耗时、路径平均长度以及路径规划的成功率。其中，通过计算末端执行器运行的距离来测量路径长度。同时，选择RRT-connect算法和RRT算法作为传统算法进行对比。为保证试验的统一性，测试不同算法时，每种采摘环境中的果实生成坐标均相同。不同算法在环境A、B和C中的试验结果如表2所示。由表2可知，对于路径规划的成功率，环境A和B中LSTM-SAC和SAC的路径规划成功率高于传统算法，环境C中仅有LSTM-SAC的路径规划成功率高于传统算法。对于路径平均长度，环境A和C中LSTM-SAC和LSTM-DDPG的路径平均长度短于传统算法，环境B中仅有LSTM-SAC的路径长度短于传统算法。对于平均规划耗时，深度强化学习算法耗时远小于传统算法，这是因为深度强化学习算法使用了神经网络来预测无碰撞路径，相较于RRT-connect和RRT需要在构型空间中获取大量样本来探索最优路径的计算量更小。

综合在3种环境中各算法的表现可知，LSTM-SAC算法在路径平均长度方面相较于SAC算法缩短了43.51%，在路径规划成功率方面提升了9.00%。相较于DDPG算法，LSTM-DDPG算法使路径平均长度缩短了33.39%，路径规划成功率提升了23.00%。另一方面，与传统算法RRT-connect相比，LSTM-SAC算法使路径平均长度缩短了16.20%，路径规划成功率提升了9.67%。

3 结论

为了实现采摘机器人野外环境的高效规划，本文提出了一种基于深度强化学习的柑橘采摘机械臂路径规划方法。于搭建的柑橘采摘仿真试验平台下3种不同的采摘环境进行仿真试验，结论如下：

1) 本文将人工势场结合到强化学习的状态中，并构建包含人工势场的奖励函数，该方法让深度强化学习算法获得更高维度的信息以学习更具体的行为策略，从而提高深度强化学习算法的训练效率和路径规划的成功率。

2) 本文将LSTM结构应用于深度强化学习的Actor网络和Critic网络中，设计了LSTM-actor和LSTM-critic网络结构。综合3种环境中的表现，相较于SAC算法，LSTM-SAC算法的采摘路径规划成功率的提升幅度达到9.00%，算法收敛速度快了53.73%，路径长度缩短了43.51%；相较于DDPG算法，LSTM-DDPG算法的采摘路径规划成功率的提升幅度达到23.00%，算法收敛速度快了57.25%，路径长度缩短了33.39%。

3) 本文将深度强化学习算法与传统算法在路径规划用时、长度和成功率方面的表现进一步对比，仿真试验结果表明，在路径规划用时方面深度强化学习算法均优于传统算法，充分表明利用神经网络可以在复杂环境中更快地搜索可行路径。其中，本文提出的LSTM-SAC算法比RRT-connect传统算法在3种环境中的路径平均长度综合缩短了16.20%，路径规划成功率综合提升了9.67%。