水稻Oryza sativa L.是我国主要粮食作物,种植过程中应适时精量施肥,以促进其长势良好,实现优质高产[1-5]。研究表明,在土壤中施入固体肥被作物吸收利用率仅为30%,施入液体肥被作物吸收利用率可达80%以上[6]。液体肥具有施肥量易于调控、排肥口堵塞率低、肥效好等优势[7],且可利用变量施肥技术提高精量施用水平。依据作物长势和土壤肥分变量调控施用液体肥,有助于节约生产成本、提升肥料利用率、减少种植环境污染[8]。在液体肥变量施用系统研究方面,目前主要基于模糊控制、PID控制等理论,采用单片机或PLC调控电磁比例调节阀的开度,实现肥料精准施用。郎春玲等[9]研制了单片机控制的深施型液体肥变量施用系统,基于处方图对电磁比例调节阀开度进行调节,室内试验的施肥精度大于95%,施肥最小误差每次为0.2 mL。田敏等[10]研制了水肥一体牵引液肥机变量施肥系统,构建了流量实时采集反馈模型,基于遗传算法对模糊控制规则进行了优化,提高了施肥精度。洪延宏[11]基于神经网络的PID变量控制算法研制了大田液肥变量喷施系统。采用电磁比例调节阀的施肥系统成本高,液肥中含有的杂质易使阀芯运动阻塞或喘动,导致系统工作不稳定[12]。刘志壮等[13]设计了由直流电机、减速器及针阀等组成的机电式流量系统,采用模糊PID控制算法,解决了变量喷雾农药流量控制问题。李加念等[14-15]改进了文丘里变量施肥装置,利用电导电极实时反馈肥液浓度,采用模糊PID算法细调电磁阀的PWM占空比,使混肥器的吸肥浓度达到目标值。李翠锦等[16]针对农田喷雾需求,采用永磁直流电动机为执行器,通过自适应模糊PID算法控制施肥量。
现有液体肥变量施用系统研究主要应用于滴灌施肥[17-18]和叶面喷肥[17,19-21],适用于水稻种植的液体肥变量施用系统的研究鲜见报道。本文基于水稻水田机械深施肥技术要求,设计一种机电式液体肥微小流量调控系统,并将该系统应用于团队已研制的水田液体肥气力引射式施肥器[22],构建水稻液体肥变量施用系统;通过仿真试验分析系统的精度和响应性能,以期为近水稻根部的小流量、低成本施肥及水稻田间液体肥变量施用技术的推广应用提供装备支持。
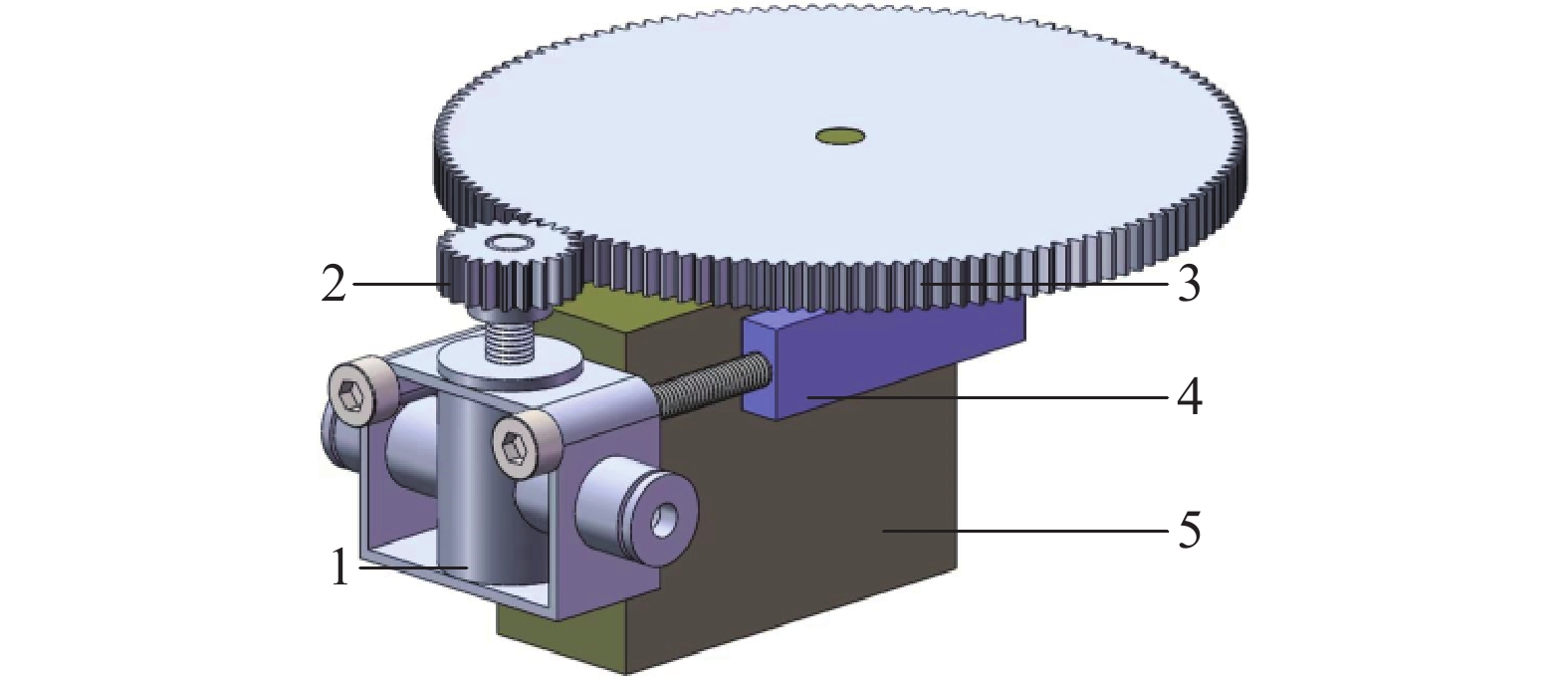
1 液体肥变量施用系统 1.1 机电式流量调节阀机电式流量调节阀是实现微小流量调控的关键执行部件,由出入口直径均为10 mm的流量调节阀、从动齿轮、主动齿轮、U型架和MG995型电动舵机组成,结构简图如图1所示。MG995型电动舵机的转角范围为0~270°,工作扭矩为1.3 N·m,响应转速为53~62 r/min,脉冲信号宽度为0.5~2.5 ms。主动齿轮的齿数为132,安装在电动舵机的输出轴末端;从动齿轮的齿数为22,安装于流量调节阀的阀芯末端;主动齿轮和从动齿轮的模数均为0.5 mm,通过齿数差实现速比为6的增速传动。
|
图 1 机电式流量调节阀 Fig. 1 Electromechanical flow regulating valve 1:流量调节阀;2:从动齿轮;3:主动齿轮;4:U型架;5:电动舵机 1: Flow regulating valve; 2: Driven gear; 3: Driving gear; 4: U-shaped frame; 5: Electric steering gear |
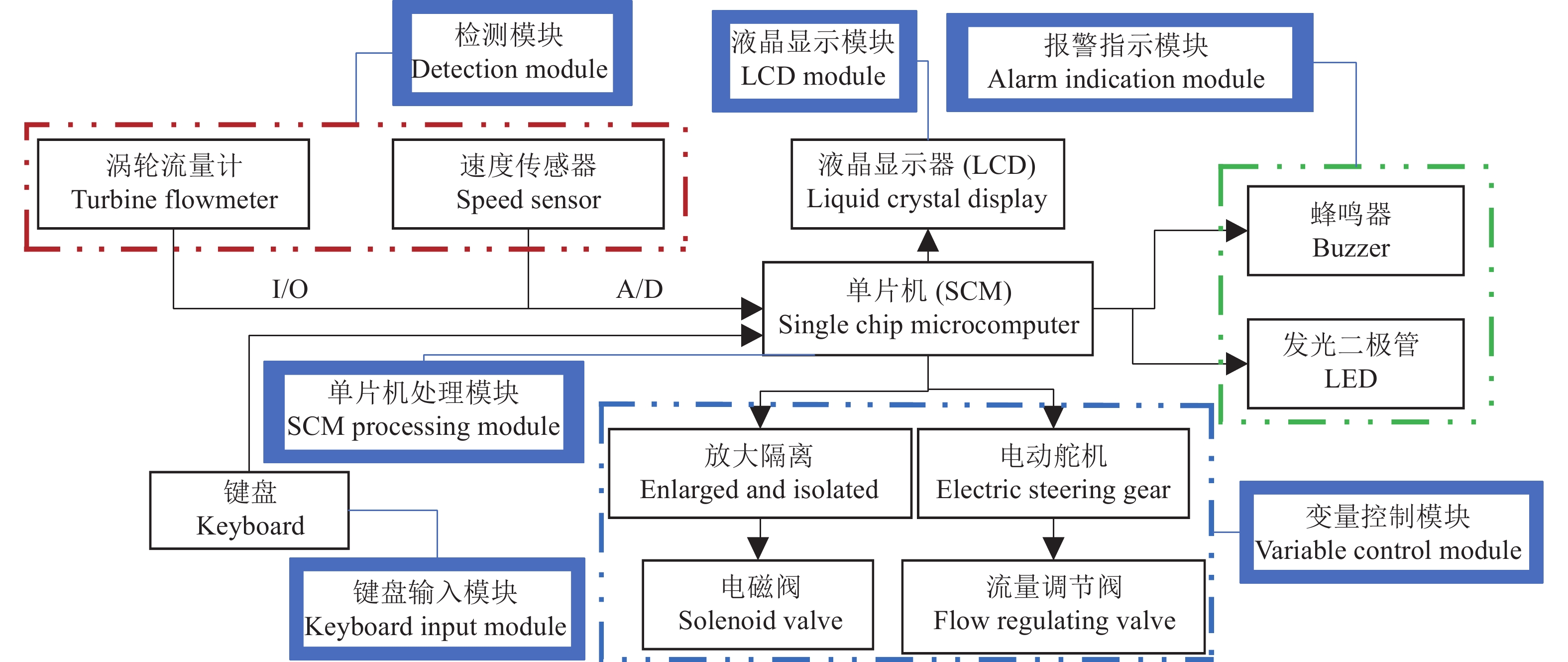
基于机电式流量阀的流量调节控制系统结构如图2所示,由单片机处理模块、变量控制模块、检测模块、液晶显示模块、键盘输入模块和报警指示模块等组成。STC89C52型单片机输出端通过舵机驱动电路与电动舵机连接,通过光耦隔离继电器与电磁阀连接;单片机输入端通过A/D转换芯片与E6B2-CWZ5B型速度传感器连接,通过I/O与MJ-HZ41C型涡轮流量计(流量范围0.15~1.50 L/min或1.92~19.20 g/s)连接。用于预设流量的键盘输入模块采用4×4矩阵键盘,由蜂鸣器和发光二极管组成的报警指示模块实现缺肥和吸肥异常报警。
|
图 2 流量调节控制系统结构框图 Fig. 2 The structure block diagram of flow regulation control system |
气力引射式施肥器可将压缩气体和液体肥进行混合,在出口形成液肥雾化射流,增大肥料与土壤的接触面积,提高土壤蓄肥能力,延缓肥料的流失速度,增加作物根系对养分的吸收利用时间,进一步提高肥料利用率,有效解决现有水田深施肥机具的堵塞问题[23]。将设计的机电式流量阀控制系统应用到气力引射式施肥器,搭建的液体肥变量施用系统样机如图3所示。压缩气体经气源处理元件清除杂质后沿输气管进入气力引射式施肥器,通过键盘将目标施肥量输入单片机,速度传感器和涡流流量计将检测的机具行进速度和吸肥管路液肥的实时流量反馈给单片机,单片机对数据进行处理,实时调整机电式流量调节阀开度和电磁阀开闭,形成闭环反馈控制,使液肥以一定的流速进入气力引射式施肥器并与压缩气体混合,最后在施肥器出口形成雾化射流,喷施到水稻根区附近土壤,实现恒量、恒深施肥作业。

|
图 3 液体肥变量施用调节系统 Fig. 3 The adjustment system for liquid fertilizer variable fertilization 1:气力引射式施肥器;2:机电式流量调节阀;3:速度传感器;4:电磁阀;5:涡轮流量计 ;6:单片机;7:电源 1:Pneumatic injection fertilizer applicator; 2: Electromechanical flow regulating valve; 3: Speed sensor; 4:Solenoid valve; 5:Turbine flowmeter; 6: Single chip microcomputer; 7: Power supply |
液体肥质量流率定义为单位时间内液体肥变量施用系统的吸肥口所卷吸的液体肥质量,是评价液体肥施用效率的重要指标。为明确机电流量调节阀开口大小对液体肥质量流率的影响,设定系统工作压力为0.3 MPa进行标定试验,试验平台如图4所示。采用电子天平(精度0.1 g)称量并记录装有液体肥肥箱的起始质量;启动恒压供气系统,当压力稳定后,将吸肥管一端插入肥箱中同时用秒表开始计时;计时结束时取出吸肥管,称量并记录肥箱的最终质量,按式(1)计算液体肥质量流率(q):

|
图 4 液体肥质量流率标定试验平台 Fig. 4 The test platform of liquid fertilizer mass flow rate calibration 1:储气罐;2:过滤减压阀;3:输气管;4:施肥器;5:吸肥管;6:液体肥肥箱;7:机电流量调节阀;8:电控箱 1: Air receiver; 2: Pressure reducing valve; 3: Gas transmission pipe; 4: Fertilizer applicator; 5: Fertilizer suction pipe; 6: Liquid fertilizer tank; 7: Electromechanical flow regulating valve; 8: Electric cabinet |
| $ q = \dfrac{{{m_1} - {m_2}}}{t}\text{,} $ | (1) |
式中,m1为液体肥肥箱的起始质量,g;m2为肥箱的最终质量,g;t为计时时间,s。
将电动舵机转角划分为10等分,通过键盘输入目标角度,每组试验控制电动舵机驱动流量调节阀运行1个等分(即舵机转动27º),分别记录各位置施肥量,每组试验计时3 min,重复3次,计算各组液体肥q平均值。
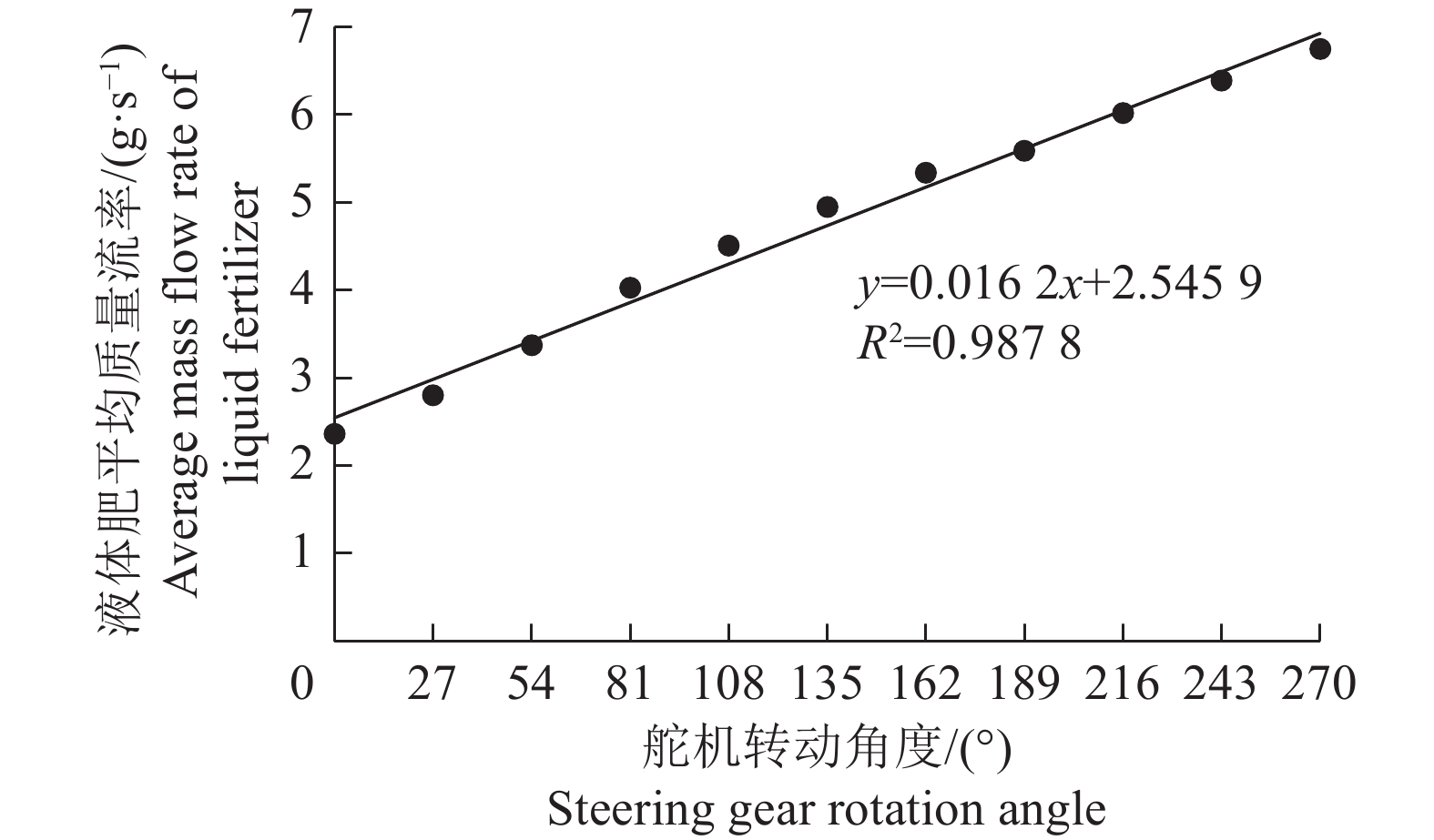
试验结果如图5所示,施肥器的液体肥q随电动舵机转动角度的增大呈线性递增,拟合度为0.987 8,在电动舵机转动范围内,液体肥q的可调节范围为2.36~6.75 g/s。
|
图 5 舵机转动角度与液体肥平均质量流率关系图 Fig. 5 Relationship between steering gear rotation angle and average mass flow rate of liquid fertilizer |
我国水稻田氮肥(纯氮)施用量平均为180 kg/hm2,液体肥施用的q应与拖拉机的前进速度相匹配,拖拉机作业速度、水稻纯氮施用量与施肥器q之间的关系如下式:
| $ q = \dfrac{{LvQ}}{{10w}}\text{,} $ | (2) |
式中,L为施肥器作业行距(一般为0.3 m),m;v为水田拖拉机的作业速度,m/s;Q为水稻纯氮施用量,kg/hm2;w为液体氮肥的氮素质量分数(本研究氮素质量分数为32%)。
2 控制器设计与仿真试验 2.1 控制系统模型设电动舵机转速为
| $ \omega = {k_1}{U_{\rm{r}}}\text{,} $ | (3) |
| $ \omega ' = {k_2}\omega = {k_1}{k_2}{U_{\rm{r}}} = {\rm{d}}\varphi /{\rm{d}}t\text{,} $ | (4) |
式中,
取
| $ \varphi = k{U_{\rm{r}}}t - {t_0}_{ } \text{,}_{ } $ | (5) |
式中,t0为电磁惯性和机械惯性。
对式(5)进行拉普拉斯变换,得到控制系统的传递函数为:
| $ {{G}}(s) = \dfrac{{k{U_{\rm{r}}}}}{{{s^2}}} - \dfrac{{{t_0}}}{s} = \dfrac{{ - {t_0}s + k{U_{\rm{r}}}}}{{{s^2}}}\text{,} $ | (6) |
实际系统中,
| $ {{G}}(s) = \dfrac{{ - 0.010s + 7.28}}{{{s^2}}} 。$ | (7) |
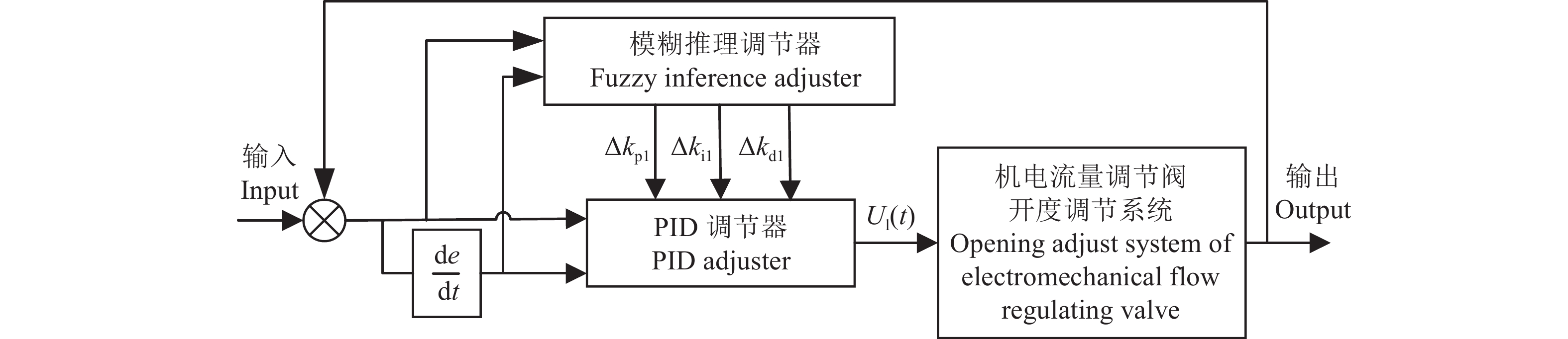
为使流量调节系统具备较强的抗外界干扰能力,基于模糊PID算法建立控制器结构如图6所示。模糊PID控制器实时监测并获取施肥器的施肥量,将其与目标施肥量比较,得到施肥量偏差(e)和偏差变化率(ec),依据模糊推理调节器实时调整PID的比例系数(kp1)、积分系数(ki1) 和微分系数(kd1) ,得到模糊PID调节器的输出量[Ul(t)] ,调控机电式流量调节阀的开度,实现液体肥变量施用控制系统参数的自适应调节[25]。
|
图 6 模糊PID控制器结构框图 Fig. 6 The structure block diagram of fuzzy PID controller |
依据模糊控制理论和预试验中积累的经验[15-16,25-27],制定控制器规则(表1)。当e较大时,为保证系统具有良好的跟踪性能,选择较大的kp1和较小的kd1,同时为了防止系统出现较大的超调量和限制积分作用,取较小的ki1值;当e较小时,为了使系统具有快速响应能力和较小的超调量,选择较小的kp1以及适当的ki1和kd1[16,26-27]。
|
|
表 1 模糊控制规则表 Table 1 Rules table of fuzzy control |
| $ {k_{{\rm{p}}1}} = {k'_{{\rm{p}}1}} + \Delta {k_{{\rm{p}}1}}_{ \text{,} } $ | (8) |
| $ {k_{{\rm{i}}1}} = {k'_{{\rm{i}}1}} + \Delta {k_{{\rm{i}}1}}\text{,} $ | (9) |
| $ {k_{{\rm{d}}1}} = {k'_{{\rm{d}}1}} + \Delta {k_{{\rm{d}}1}}_{ \text{,}} $ | (10) |
式中,
采用临界比例度法获得临界比例度(δK)和临界振荡周期(TK),按照以下PID控制参数经验公式,得到PID控制器的比例系数初始值(KP)、积分系数初始值(KI)和微分系数初始值(KD)等参数[28]。
| $ {K_{\text{P}}} = \dfrac{1}{{1.7{\delta _{\text{K}}}}}\text{,} $ | (11) |
| $ {T_{\text{I}}} = 0.5{T_{\text{K}}}\text{,} $ | (12) |
| $ {T_{\text{D}}} = 0.125{T_{\text{K}}}\text{,} $ | (13) |
| $ {K_{\text{I}}} = \dfrac{{K_{\text{P}}}T}{{{T_{\text{I}}}}}\text{,} $ | (14) |
| $ {K_{\text{D}}} = \dfrac{{{{K_{\text{P}}}T_{\text{D}}}}}{T}\text{,} $ | (15) |
式中,T为采样时间,TI为积分时间,TD为微分时间。按式(11)~(15)计算,得到PID控制器参数为:
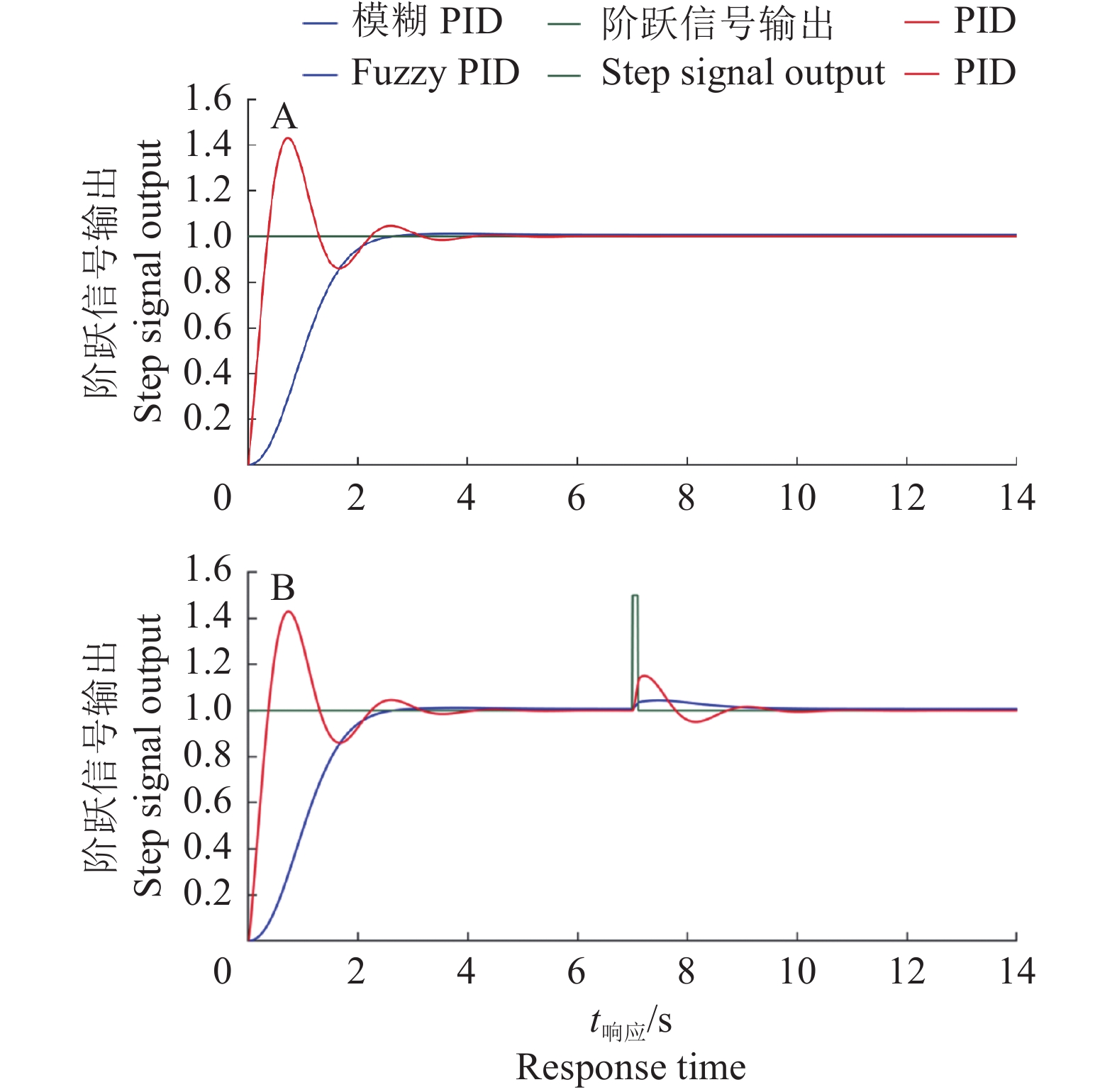
仿真试验采用Matlab软件(2021b版)的Simulink仿真模块构建控制器仿真模型,如图7所示。控制系统的单位阶跃响应仿真结果如图8A所示。PID控制器的响应曲线超调量为42.90 %,调节时间为4.44 s,稳态误差为0.010;模糊PID控制器的响应曲线超调量为0.12%,调节时间为2.51 s,稳态误差为0.007。表明模糊PID控制能获得更优的动态调节和稳定性能。
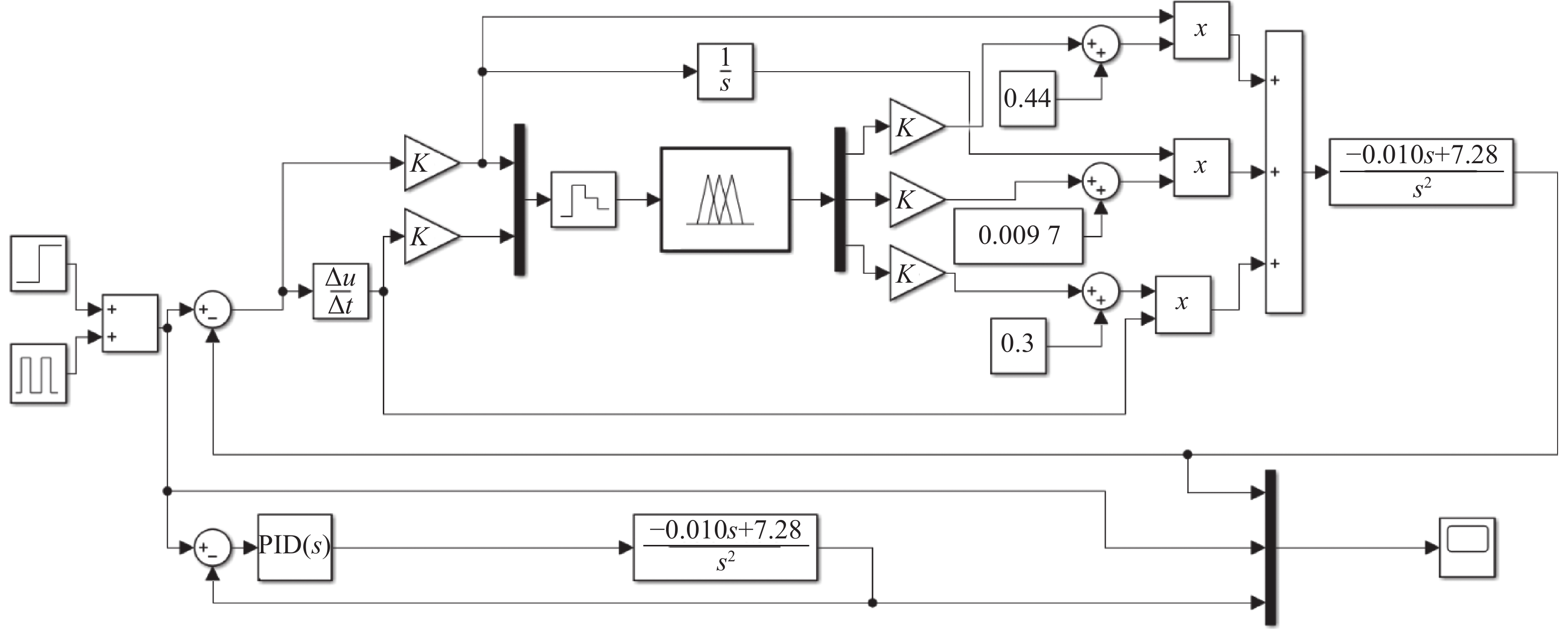
|
图 7 控制系统仿真模型 Fig. 7 The simulation model of control system |
为模拟控制器受到的干扰情况,在实时流量稳定时段的7 s处添加1个幅值为0.5,持续时间0.1 s的干扰脉冲,控制系统响应仿真结果如图8B所示。在加入脉冲信号之后,模糊PID控制系统与PID控制系统均发生了突变,PID控制器的调节时间为1.67 s,模糊PID控制器的调节时间为0.61 s。表明模糊PID控制震荡延续时间短,能快速回归稳态,具有更强的抗干扰能力。
|
图 8 单位阶跃(A)和加干扰脉冲(B)的响应仿真图 Fig. 8 Simulation diagrams of unit step response(A) and impulse response with interference(B) |
搭建水稻液体肥变量施用试验平台(图9)。将液体肥变量施用系统搭载在东风井关PG6乘坐式水田拖拉机上,流量调节控制系统置于拖拉机前端,气力引射式吸肥器安装在拖拉机尾部,供气系统由空压机、储气罐、气源处理元件、减压阀、压力表和输气管路等组成,其输出气管与气力引射吸肥器的入气口连接。选用广东绿兴生物科技有限公司生产的液态氮肥(氮质量分数为32%),分别采用PID和模糊PID控制器对液体肥变量施用系统的质量流率控制精度和跟踪性能进行试验对比。

|
图 9 系统性能试验平台 Fig. 9 Experiment platform of system performance |
以标定试验确定的液体肥质量流率调节范围2.36~6.75 g/s为依据,设计质量流率控制精度试验。在水田拖拉机静止条件下调节试验平台吸肥管路压力为0.3 MPa,在2.8~5.0 g/s范围内设置10种目标施肥质量流率,记录3 min内每种目标施肥质量流率条件下的实际施肥质量流率,每组试验重复3次。分别统计各种目标施肥质量流率重复试验中实测施肥质量流率(qi)的平均值(qm),qm相对目标施肥质量流率(qb)的绝对误差(Δqm),以及质量流率控制精度(P)。计算公式如下:
| $ {q_{\text{m}}} = \displaystyle\sum\limits_{i = 1}^3 {{q_{i}}} \text{,} $ | (16) |
| $ \Delta {q_{\text{m}}} = \left| {{q_{\text{b}}} - {q_{\text{m}}}} \right|\text{,} $ | (17) |
| $ P = \dfrac{{{q_{\text{b}}} - \Delta {q_{\text{m}}}}}{{{q_{\text{b}}}}} \times 100{\text{%}} 。$ | (18) |
液体肥质量流率在调节范围2.36~6.75 g/s内升高或降低,以验证液体肥变量施用系统质量流率跟踪性能。具体方法为:调节拖拉机作业速度为0.6 m/s,吸肥管路压力为0.3 MPa,调整机电流量调节阀的开度,先将施肥质量流率从0升高至3 g/s,质量流率稳定后再从3 g/s升高至5 g/s,质量流率稳定后又从5 g/s降低至4 g/s,以1 Hz频率采集实时质量流率,每组试验重复3次。以3次质量流率跟踪试验的超调量、上升时间、调节时间、峰值时间的平均值作为质量流量率跟踪性能的评价指标。
3.2 结果与分析 3.2.1 质量流率控制性能质量流率控制性能试验结果如表2所示。在10种目标质量流率条件下,PID控制的质量流率绝对误差范围为0.20~0.35 g/s,模糊PID控制的质量流率绝对误差范围为0.15~0.19 g/s;在各目标质量流率条件下,采用模糊PID控制的质量流率绝对误差均低于PID控制。从控制精度角度比较,PID控制精度最高为95.21%、最低为90.00%,模糊PID控制精度最高为96.88%、最低为93.93%,表明本文设计的模糊PID控制系统具有更高的质量流率控制精度,能够更好地满足田间施肥作业精准性能要求。
|
|
表 2 模糊PID和PID控制系统的质量流率控制精度试验结果 Table 2 Experiment result of control accuracy of mass flow rate for fuzzy PID and PID controlling systems |
图10的结果表明,当质量流率为3 g/s时,模糊PID控制超调量为16.6%,比PID控制低6.7%;上升时间为1.8 s,比PID控制少0.9 s;调节时间为12 s,比PID控制少2 s。当质量流率为4 g/s时,模糊PID控制的超调量为10.0%,比PID控制低5.0%;调节时间为9 s,比PID控制少5 s。当质量流率为5 g/s时,模糊PID控制的超调量为10.0%,比PID控制低4.0%;上升时间为1.8 s,比PID控制少0.9 s;调节时间为11 s,比PID控制少1 s。模糊PID控制的超调量平均值为12.2%,上升时间平均值为1.5 s,调节时间平均值为10.7 s,峰值时间平均值为1.7 s;PID控制的超调量平均值为17.4%,上升时间平均值为2.1 s,调节时间平均值为13.3 s,峰值时间的平均值为2.3 s。表明在系统设定的施肥量发生连续变化时,模糊PID控制具有更快的响应速度和更高的鲁棒性。
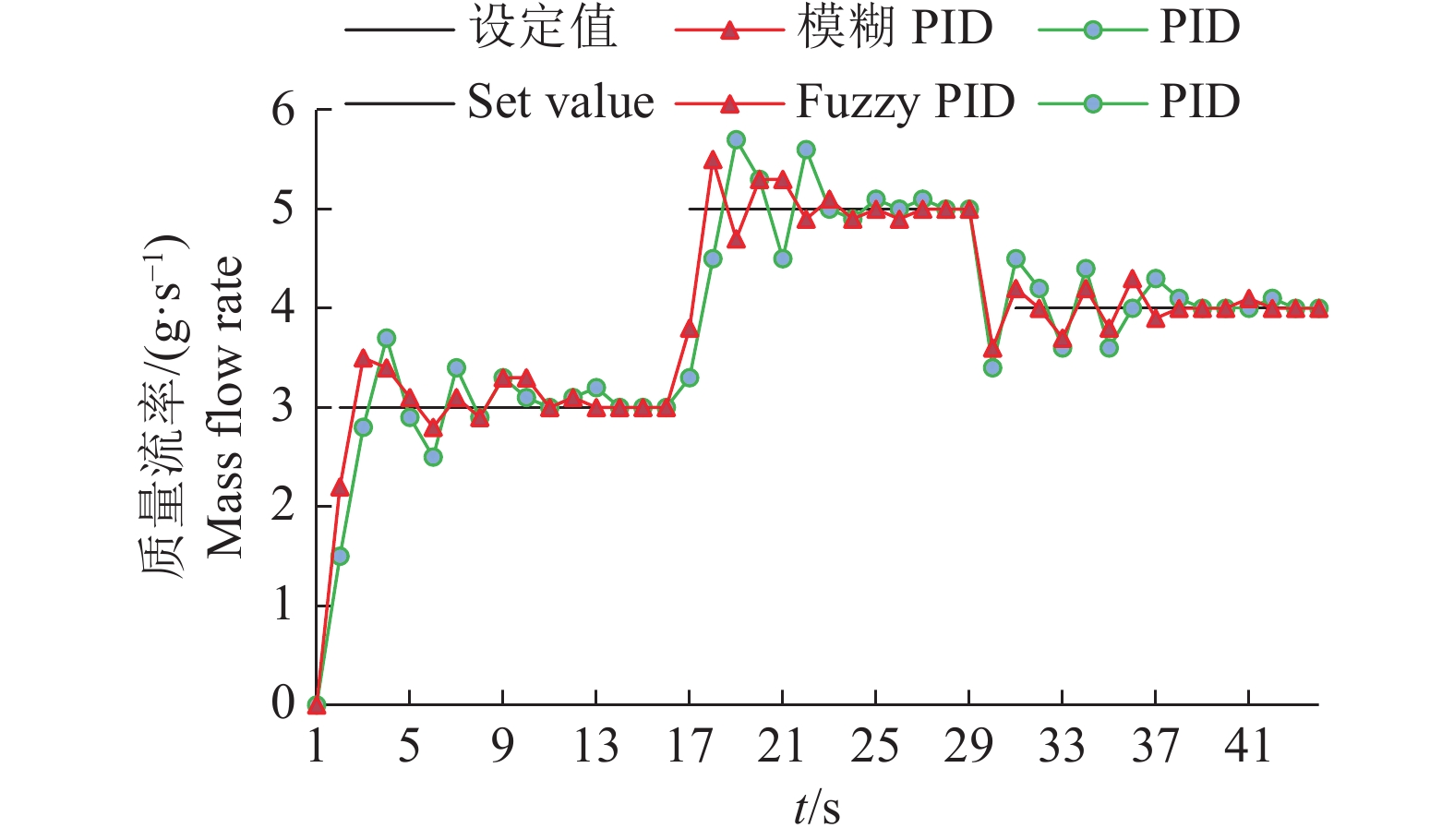
|
图 10 质量流率跟踪性能 Fig. 10 The tracking performance of mass flow rate |
1)设计了一种基于单片机控制的机电式微小流量调节阀,应用于已研制的气力引射式施肥器,构建了水稻液体肥变量施用系统,在吸肥管路工作压力为0.3 MPa的条件下进行标定试验,确定液体肥质量流率的可调节范围为2.36~6.75 g/s。
2)设计了水稻液体肥变量施用模糊PID控制器,并与PID控制器的调控性能进行了仿真对比。结果表明,模糊PID控制器的阶跃信号响应超调量、调节时间和稳态误差分别为0.12%、2.51 s和0.007,PID控制器的阶跃信号响应结果分别为42.90%、4.44 s和0.010,模糊PID控制器具有更好的动态调节和稳定性能;在流量稳定时段7 s处添加幅值为0.5、持续时间为0.1 s的干扰脉冲时,模糊PID控制器调节时间为0.61 s,相比PID控制器1.67 s的震荡时间更短,具有更强的抗干扰能力。
3)在10种目标质量流率条件下,模糊PID的质量流率绝对误差均低于PID控制,PID的控制精度为 90.00%~95.21%,而模糊PID的控制精度为93.93%~96.88%,具有更高的精准调控能力;在施肥量变化时,模糊PID控制的超调量、上升时间和调节时间均低于PID控制,模糊PID控制的超调量、上升时间、调节时间和峰值时间平均值分别为12.2%、1.5 s、10.7 s和1.7 s,PID控制相应的平均值分别为17.4%、2.1 s、13.3 s和2.3 s,表明模糊PID控制具有更快的响应性和更高的鲁棒性。
| [1] |
孙浩燕, 李小坤, 任涛, 等. 浅层施肥对水稻苗期根系生长及分布的影响[J]. 中国农业科学, 2014, 47(12): 2476-2484. DOI:10.3864/j.issn.0578-1752.2014.12.020 (  0) 0) |
| [2] |
朱元宏, 赵峥, 张翰林, 等. 不同施肥方式对水稻农艺性状及产量的影响[J]. 上海交通大学学报(农业科学版), 2014, 32(1): 43-48. (  0) 0) |
| [3] |
杨亨东. 基于精准农业设计的水稻施肥系统开发[J]. 农机化研究, 2017, 39(7): 134-136. DOI:10.3969/j.issn.1003-188X.2017.07.027 (  0) 0) |
| [4] |
孙芝文. 水稻施肥技术对产量的影响[J]. 河南农业, 2017(17): 30-31. DOI:10.15904/j.cnki.hnny.2017.17.009 (  0) 0) |
| [5] |
陈金, 赵斌, 衣淑娟, 等. 我国变量施肥技术研究现状与发展对策[J]. 农机化研究, 2017, 39(10): 1-6. DOI:10.13427/j.cnki.njyi.2017.10.001 (  0) 0) |
| [6] |
黄燕, 汪春, 衣淑娟. 液体肥料的应用现状与发展前景[J]. 农机化研究, 2006, 28(2): 198-200. DOI:10.3969/j.issn.1003-188X.2006.02.072 (  0) 0) |
| [7] |
冯金龙, 周文琪, 唐汉, 等. 液肥注射式变形齿轮扎穴机构设计与试验[J]. 东北农业大学学报, 2017, 48(2): 90-96. DOI:10.3969/j.issn.1005-9369.2017.02.012 (  0) 0) |
| [8] |
梁春英, 衣淑娟. 液体肥变量施用控制系统性能的试验研究[J]. 农机化研究, 2010, 32(8): 117-120. DOI:10.3969/j.issn.1003-188X.2010.08.031 (  0) 0) |
| [9] |
郎春玲, 王金武, 王金峰, 等. 深施型液态肥变量施肥控制系统[J]. 农业机械学报, 2013, 44(2): 43-47. DOI:10.6041/j.issn.1000-1298.2013.02.009 (  0) 0) |
| [10] |
田敏, 白金斌, 李江全. 基于遗传算法的液肥变量施肥控制系统[J]. 农业工程学报, 2021, 37(17): 21-30. DOI:10.11975/j.issn.1002-6819.2021.17.003 (  0) 0) |
| [11] |
洪延宏. 基于神经网络算法的液肥喷施变量控制系统研发与应用[D]. 石河子: 石河子大学, 2020.
(  0) 0) |
| [12] |
杨旸. 液压电磁比例调节阀常见故障处理[J]. 设备管理与维修, 2010(1): 31-32. DOI:10.3969/j.issn.1001-0599.2010.01.020 (  0) 0) |
| [13] |
刘志壮, 洪添胜, 张文昭, 等. 机电式流量阀的模糊控制实现与测试[J]. 农业工程学报, 2010, 26(13): 22-26. (  0) 0) |
| [14] |
李加念, 洪添胜, 冯瑞珏, 等. 基于脉宽调制的文丘里变量施肥装置设计与试验[J]. 农业工程学报, 2012, 28(8): 105-110. DOI:10.3969/j.issn.1002-6819.2012.08.016 (  0) 0) |
| [15] |
李加念, 洪添胜, 冯瑞珏, 等. 基于模糊控制的肥液自动混合装置设计与试验[J]. 农业工程学报, 2013, 29(16): 22-30. DOI:10.3969/j.issn.1002-6819.2013.16.004 (  0) 0) |
| [16] |
李翠锦, 周树林, 宋乐鹏. 基于模糊PID的变量液体施肥控制系统[J]. 农机化研究, 2019, 41(3): 244-249. DOI:10.3969/j.issn.1003-188X.2019.03.045 (  0) 0) |
| [17] |
邓兰生, 涂攀峰, 叶倩倩, 等. 滴施液体肥对甜玉米生长、产量及品质的影响[J]. 玉米科学, 2012, 20(1): 119-122. DOI:10.3969/j.issn.1005-0906.2012.01.024 (  0) 0) |
| [18] |
杨军. 滴灌变量精准控制施肥装置设计与实现[D]. 石河子: 石河子大学, 2016.
(  0) 0) |
| [19] |
BAI J, TIAN M, LI J. Control system of liquid fertilizer variable-rate fertilization based on beetle antennae search algorithm[J]. Processes, 2022, 10(357): 1-14. DOI:10.3390/pr10020357 (  0) 0) |
| [20] |
YAMIN M, ISMAIL W I B, AZIZ S A, et al. Design considerations of variable rate liquid fertilizer applicator for mature oil palm trees[J]. Precision Agriculture, 2022, 23: 1413-1448. DOI:10.1007/s11119-022-09892-5 (  0) 0) |
| [21] |
FU J, CHEN C, ZHAO R Q, et al. Accurate variable control system for boom sprayer based on auxiliary antidrift system[J]. Journal of Sensors, 2020(8037046): 1-8. (  0) 0) |
| [22] |
王聪. 液体肥施肥器变量调节系统研究[D]. 广州: 华南农业大学, 2018.
(  0) 0) |
| [23] |
陈彬. 水田气力引射式液肥深施装置研究[D]. 广州: 华南农业大学, 2018.
(  0) 0) |
| [24] |
李益华. 自动控制原理[M]. 长沙: 湖南大学出版社, 2004: 17-22.
(  0) 0) |
| [25] |
高礼科, 倪福生, 蒋爽. 基于模糊PID控制器的旋流泵调速控制[J]. 自动化与仪表, 2020, 35(12): 72-76. (  0) 0) |
| [26] |
王健, 谢南, 黄春营. 基于模糊控制理论的温室葡萄种植灌溉算法[J]. 江苏农业科学, 2017, 45(14): 184-188. (  0) 0) |
| [27] |
苏兴华. 基于模糊控制理论的PID控制器设计[J]. 中国管理信息化, 2019, 22(3): 136-139. DOI:10.3969/j.issn.1673-0194.2019.03.055 (  0) 0) |
| [28] |
王在英, 刘魏霞, 彭倩. 过程控制系统与仪表[M]. 北京: 机械工业出版社, 2004: 190-192.
(  0) 0) |
 2023, Vol. 44
2023, Vol. 44


